高校数学をCinderellaで:2次関数のグラフ(2):平行移動
${y=a(x-p)^2+q}$ のグラフは,${y=ax^2}$ のグラフを x軸方向にp,y軸方向にqだけ平行移動したものです。
さて,これをどのようにして学び,理解すればよいでしょうか。
教科書では,まず y軸方向への平行移動,つぎに x 軸方向への平行移動を学びますが,値の表を作って考えるようになっています。つぎの図は数研出版のものですが,他社の教科書も同様です。
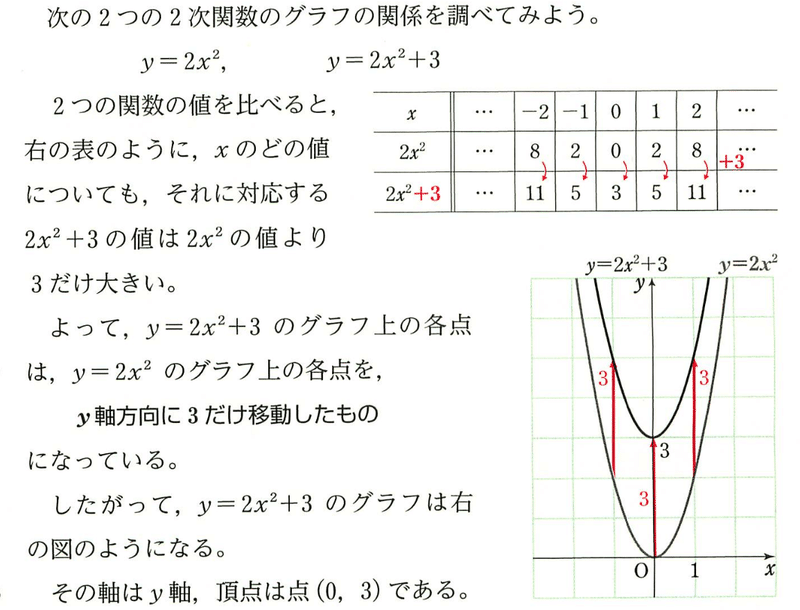
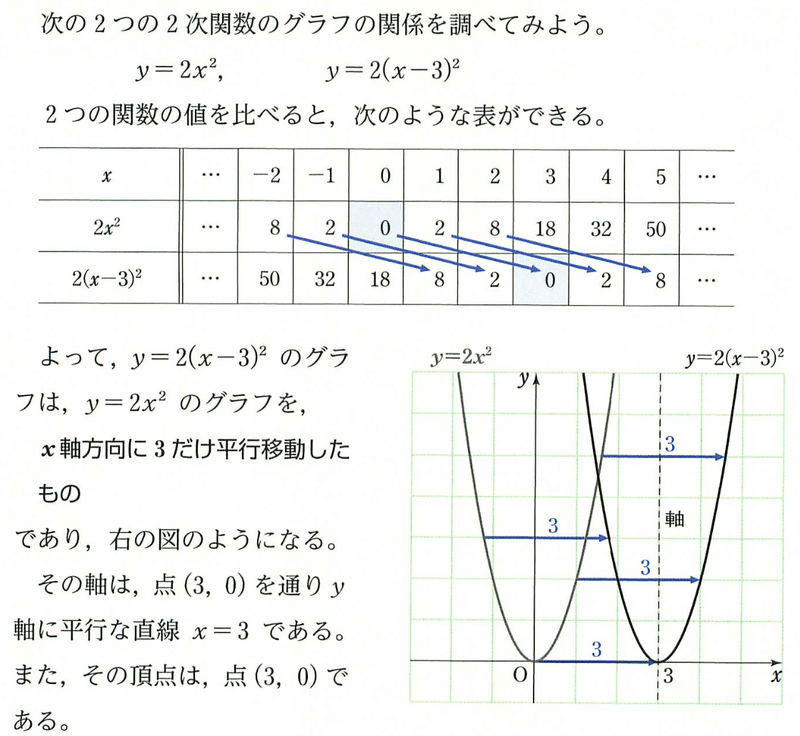
y軸方向への平行移動は直感的にも分かりやすいのですが,x軸方向への平行移動がわかりにくいのです。${2(x+3)^2}$ ではなく ${2(x-3)^2}$ と,マイナスになるからです。
このやりかたでは,結局,「値を比較するとこうなる」としかできないのです。「こうなる」の次は「覚えよう」になり,「なぜこうなるのか(マイナスになる理由)」は考えないからです。
「なぜこうなるのか」は,このもうすこしあとで学ぶのですが,そう簡単ではありません。y軸方向を直感的に「+3」 とすると,x軸方向が「-3」になる理由が説明できないからです。しかも,あとで学ぶ箇所はおまけみたいな扱いで,きちんと理解されないままになりがちです。ここをきちんと理解すれば,その後の三角関数や指数関数,対数関数のグラフでも役に立つのですが。
ここで,まったく新しいアプローチをしてみましょう。紙の教科書では絶対にできないアプローチです。つぎのリンクを開きましょう。
リンクを開くと次の画面になります。
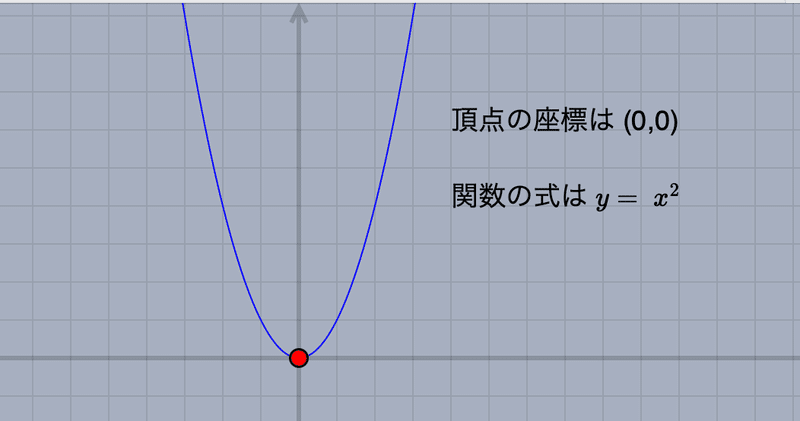
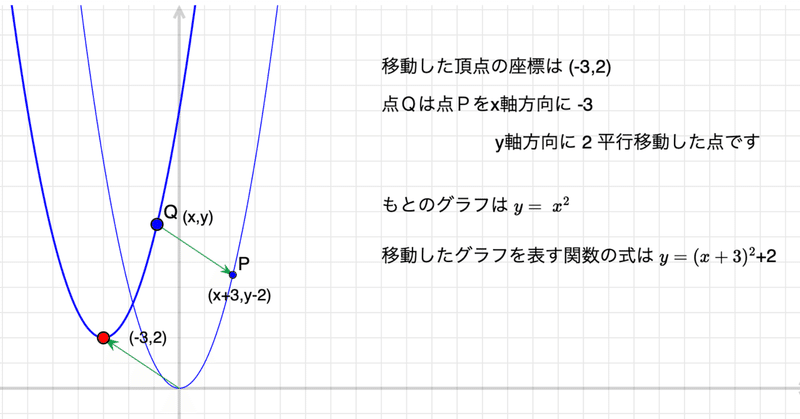
赤い点は放物線の頂点です。これを平行移動すると,グラフ全体が平行移動し,頂点の座標とそのグラフが表す2次関数の式が表示されます。
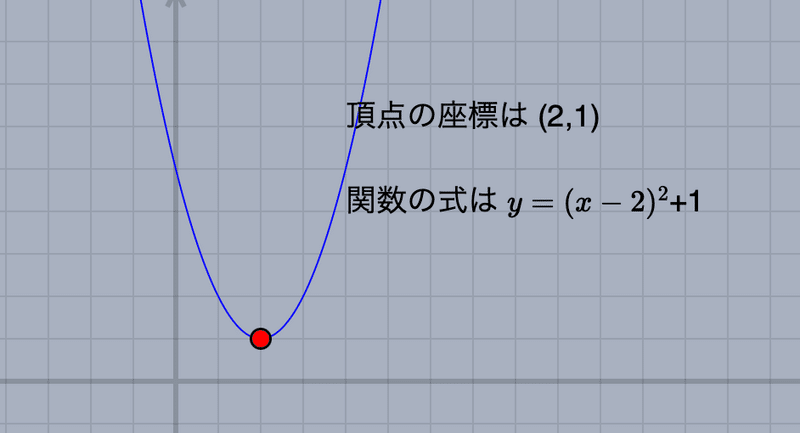
いろいろ動かした(現象を観察した)ならば,「なぜ式がそうなるのか」を考えましょう。頂点の座標との関係はすぐわかるでしょう。問題は,「なぜxのところはマイナスでyにはプラスになるのか」です。
前述のように,教科書にはその説明がありますが,そう簡単ではありません。
これがわかるためには「関数${y=f(x)}$のグラフとは,xの値と,対応するyの値を座標とする点${[x,y]}$の集合である」ということがちゃんとわかっていなければなりません。いいかえると,「グラフ上の点は ${y=f(x)}$ を満たす」ということです。
そのことを,図を動かしながら考えるのです。そのために別の図が必要です。
ではCinderella で,これらの教材を作りましょう。
まずはじめのものです。
はじめに,画面下の磁石アイコンをクリックして座標軸と方眼を表示し,スナップモードにしておきましょう。
作図ツールで原点に点を一つとり(点A),あとは次のスクリプトをCindyScriptエディタのDrawスロットに書きます。
p = A.x;
q = A.y;
f(x):= (x-p)^2+q;
plot(f(x));
str = "関数の式は $y=";
if(p == 0,
str = str + "x^2$";
);
if(p < 0,
str = str + "(x+" + (-p) + ")^2$";
);
if(p > 0,
str = str + "(x-"+p+")^2$";
);
if(q < 0,
str = str + "-" + (-q);
);
if(q > 0,
str = str + "+" + q;
);
drawtext([4, 6], "頂点の座標は ("+p+","+q+")",size->18);
drawtext([4, 4], str, size->18);やっていることはわかりますね。点Aの座標から平行移動量 p , q を取得し,式を作っています。
インスペクタで点Aのラベルを非表示にしておきましょう。

次に,2番目の平行移動量と対応する点の関係を表示するものです。今のものに追加します。
まず,頂点のAを適当なところに移動しておきます。作図ツールの「線分を加える」で点Aと原点を結んだ線分を描きます。原点はBになるでしょう。また線分CDを適当なところに描きます。
インスペクタを開き,描いた線分を選択して(描いた直後ならCDが選択されています)「特別な表示方法」で矢線にします。このときDからCに向けます。矢印の大きさはすこし小さくしましょう。もうひとつ,線分ABを選択して,こんどはBからAに向かう矢線にします。
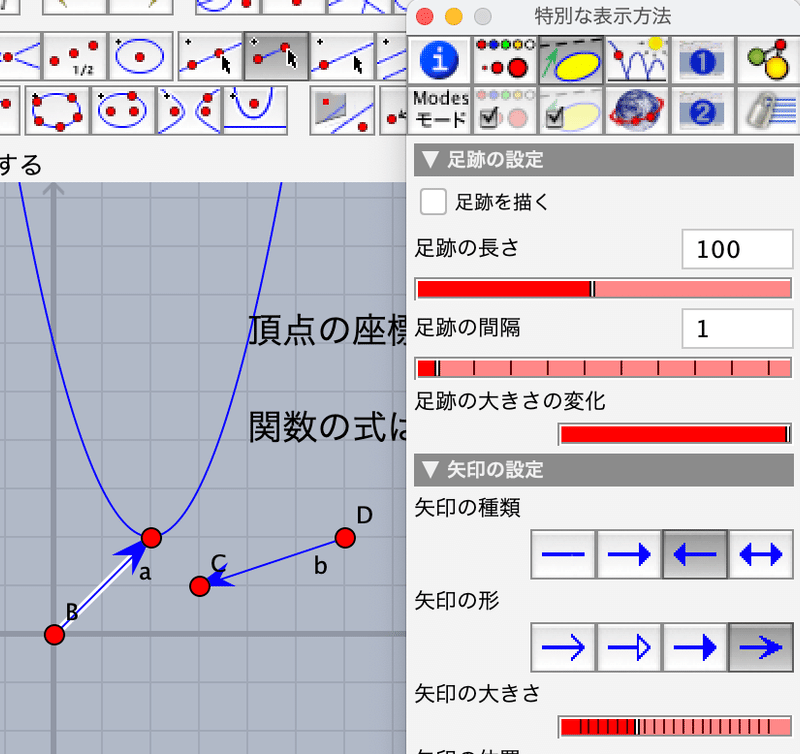
次に「要素の情報」で点CとDのラベルをPとQにかえておきます。
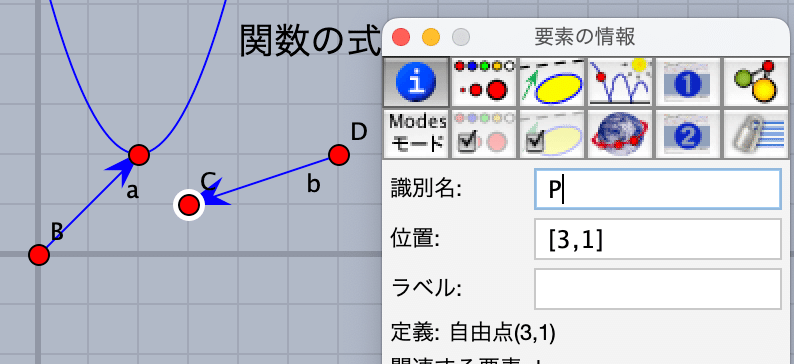
スクリプトを変更,追加します。画面に表示していた文字列「str」の最初の設定と,「頂点の座標」「関数の式」表示のところを変えます。改めて全体を示します。
p = A.x;
q = A.y;
f(x):= (x - p)^2 + q;
plot(f(x), size->2);
str = "移動したグラフを表す関数の式は $y=";
if(p == 0,
str = str + "x^2$";
);
if(p < 0,
str = str + "(x+" + (-p) + ")^2$";
);
if(p > 0,
str = str + "(x-" + p + ")^2";
);
if(q < 0,
str = str + "-" + (-q);
);
if(q > 0,
str = str + "+" + q;
);
str = str + "$";
plot(x^2);;
Q.y = f(Q.x);
P.xy = Q.xy - [p, q];
if(p > 0,sx = "-",sx = "+");
if(q > 0,sy = "-",sy = "+");
drawtext(P.xy - [1, 1], "(x" + sx+abs(p) + ",y" + sy + abs(q) + ")", size->16);
drawtext(Q.xy + [1, 0.1], "(x,y)", size->16);
drawtext(A.xy + [1, -0.2], "(" + p + "," + q + ")", size->16);
drawtext([8, 12.5], "移動した頂点の座標は (" + p + "," + q + ")", size->18);
drawtext([8, 11],"点Qは点Pをx軸方向に " + p, size->18);
drawtext([12.5, 9.5],"y軸方向に " + q + " 平行移動した点です", size->18);
drawtext([8, 7],"もとのグラフは $y=x^2$", size->18);
drawtext([8, 5], str, size->18);最後に,画面の背景色などの体裁を整えます。
HTMLに書き出して,今度は画面にも説明を表示するために,HTMLファイルの<body>の部分に説明文を追加します。
<body>
<br>
頂点とグラフ上の点Qをそれぞれドラッグしてみましょう。<br>
頂点の座標と,平行移動量,Pの座標はどのように変わりますか。<br>
点Pは y=x² のグラフ上にあります。<br>
これらのことから,平行移動すると関数の式がどうかわるのか<br>
なぜそのように変わるのかを考えましょう。<br>
<div id="CSCanvas"></div>
</body>
できあがりはこちら。
次のような画面になります。
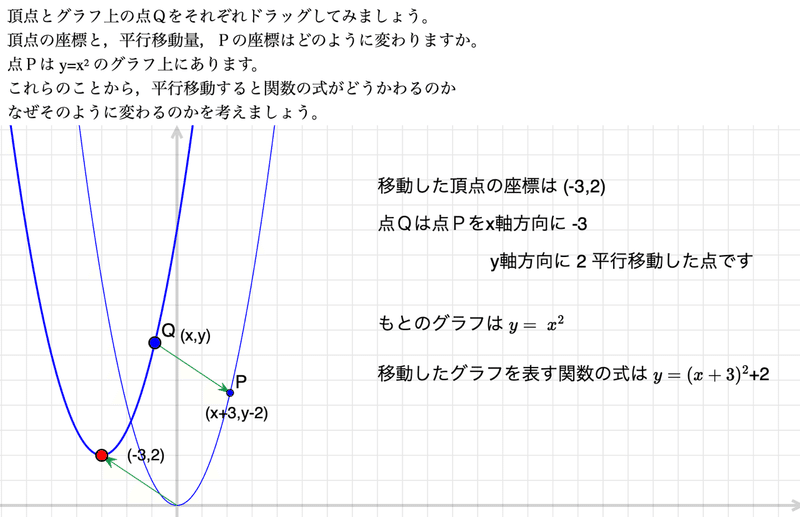
何をすればよいかの説明文が書かれていますが,これだけでは不十分でしょう。教師が説明用に使うか,生徒に動かしながら考えさせるか,使い方次第です。
