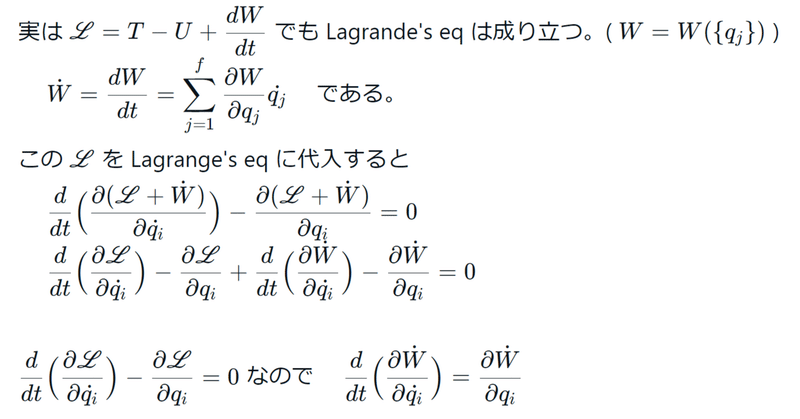
Lagrandian の不定性
$${\mathscr{L}=T-U}$$と定義されるが、
実は$${\mathscr{L}=T-U+\dfrac{dW}{dt}}$$でも Lagrande's eq は成り立つ。($${W=W(\{q_j\})}$$)
$${\dot{W}=\dfrac{dW}{dt}=\displaystyle\sum_{j=1}^f\dfrac{\partial W}{\partial q_j}\dot{q_j}}$$ である。
この$${\mathscr{L}}$$を Lagrange's eq に代入すると
$${\dfrac{d}{dt}\Big(\dfrac{\partial(\mathscr{L}+\dot{W})}{\partial\dot{q_i}}\Big)-\dfrac{\partial(\mathscr{L}+\dot{W})}{\partial q_i}=0}$$
$${\dfrac{d}{dt}\Big(\dfrac{\partial\mathscr{L}}{\partial\dot{q_i}}\Big)-\dfrac{\partial\mathscr{L}}{\partial q_i}+\dfrac{d}{dt}\Big(\dfrac{\partial\dot{W}}{\partial\dot{q_i}}\Big)-\dfrac{\partial\dot{W}}{\partial q_i}=0}$$
$${\dfrac{d}{dt}\Big(\dfrac{\partial\mathscr{L}}{\partial\dot{q_i}}\Big)-\dfrac{\partial\mathscr{L}}{\partial q_i}=0}$$なので $${\dfrac{d}{dt}\Big(\dfrac{\partial\dot{W}}{\partial\dot{q_i}}\Big)=\dfrac{\partial\dot{W}}{\partial q_i}}$$
左辺$${=\dfrac{d}{dt}\Big(\dfrac{\partial\dot{W}}{\partial\dot{q_i}}\Big)}$$
$${=\dfrac{d}{dt}\Big\{\dfrac{\partial}{\partial\dot{q_i}}\Big(\dfrac{dW}{dt}\Big)\Big\}=\dfrac{d}{dt}\Big\{\dfrac{\partial}{\partial\dot{q_i}}\Big(\displaystyle\sum_{j=1}^f\dfrac{\partial W}{\partial q_j}\dot{q_j}\Big)\Big\}=\dfrac{d}{dt}\Big(\dfrac{\partial W}{\partial q_i}\Big)}$$
$${=\displaystyle\sum_{j=1}^f\dfrac{\partial}{\partial q_j}\Big(\dfrac{\partial W}{\partial q_i}\Big)\dot{q_j}=\displaystyle\sum_{j=1}^f\dfrac{\partial^2W}{\partial q_j \partial q_i}\dot{q_j}}$$
右辺$${=\dfrac{\partial\dot{W}}{\partial q_i}}$$
$${=\dfrac{\partial}{\partial q_i}\Big(\dfrac{dW}{dt}\Big)=\dfrac{\partial}{\partial q_i}\Big(\displaystyle\sum_{j=1}^f\dfrac{\partial W}{\partial q_j}\dot{q_j}\Big)}$$
$${=\displaystyle\sum_{j=1}^f\dfrac{\partial^2W}{\partial q_i\partial q_j}\dot{q_j}=\displaystyle\sum_{j=1}^f\dfrac{\partial^2W}{\partial q_j \partial q_i}\dot{q_j}}$$
(Schwarzsche の定理より 偏微分順序を入れ替える)
よって 左辺=右辺
$${\mathscr{L}=T-U+\dfrac{dW}{dt}}$$でも Lagrange's eq は成り立つ。
この$${W(\{q_i\})}$$ を母関数(generator)と呼ぶ。
この記事が気に入ったらサポートをしてみませんか?
