物体がある曲線上を摩擦なしで重力だけが働く条件ですべり降りるときの速度が最も速くなるものを最速降下曲線という。この問題は変分法（Eulerの微分方程式）を使って解くことができ、その曲線はサイクロイドであることが知られている。
日本の江戸時代初期にあたる1600年代に解法を巡ってヨハン・ベルヌーイ、ロピタル、兄のヤコブ、ライプニッツ、ニュートンら巨人たちの確執があったことでも有名である。（詳しくはかぎしっぽを参照）

以下に求め方を示す。
（参考書、ネットでたくさんの資料を調べたが、微分方程式の導出後は天下りで「答はサイクロイドです」とあったり、式の変形が大幅に端折られていたりが多かった。やれやれ）
$${(ds)^2=(dx)^2+(dy)^2}$$より$${ds}$$を、エネルギー保存の法則より$${v}$$を求め、
所要時間$${dt=\dfrac{距離}{速さ}=\dfrac{ds}{v}=\sqrt{\dfrac{1+y'^2}{2gy}}dx}$$を求める。
これを積分して
　$${t=\displaystyle\int_0^t dt=\dfrac{1}{\sqrt{2g}}\displaystyle\int_0^x \sqrt{\dfrac{1+y'^2}{y}}dx}$$となる。
この値(汎関数)が極値を取る関数$${y}$$を求める。（変分法）
Eulerの微分方程式①に代入し、$${2y''y+y'^2+1=0}$$②を得る。

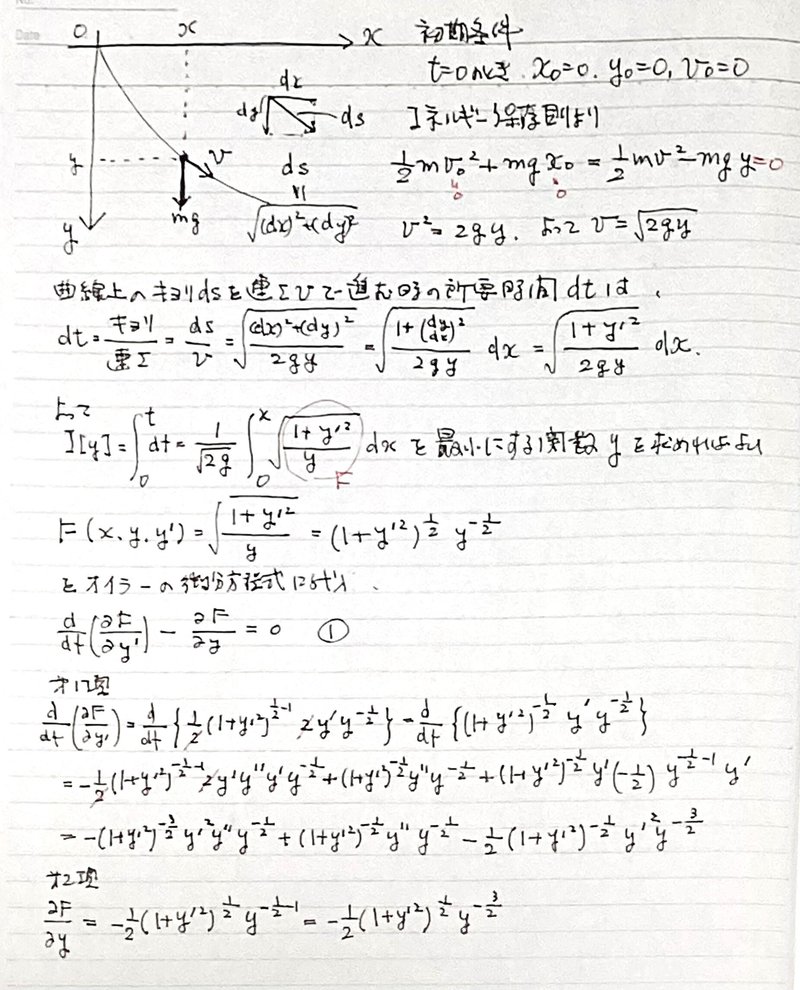
$${2y''y+y'^2+1=0}$$②は$${y,  y',  y''}$$を含む微分方程式であるが、ここで$${y'=p}$$と置き換えて積分し、最後に$${p}$$を元に戻すと$${y'=\sqrt{\dfrac{a-y}{y}}}$$③が得られる。

$${y'=\sqrt{\dfrac{a-y}{y}}}$$③の$${y}$$をそれと同じ値域（$${0\leqq y\leqq a}$$）になる関数
$${y=\dfrac{1}{2}a(1-\cos\theta)}$$④と置き換える。
$${dx=\dfrac{a}{2}\sin\theta\sqrt{\dfrac{1-\cos\theta}{1+\cos\theta}}  d\theta}$$という複雑な形になるが$${\theta}$$の半角化を行うと、積分できる形（$${dx=\dfrac{a}{2}(1-\cos\theta)}$$）になる。　
これを積分し④とあわせて書き直すと
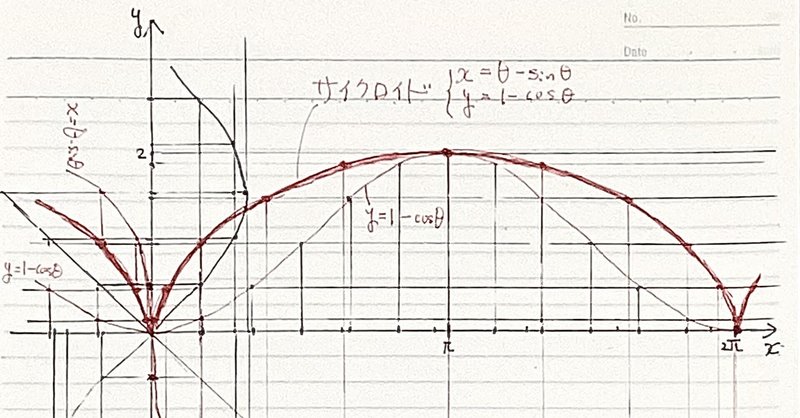
サイクロイドの式
$${x=A(\theta-\sin\theta)}$$、$${y=A(1-\cos\theta)}$$　が得られる。

サイクロイド曲線を作図してみた。

サイクロイドが一番速い。一目瞭然である。