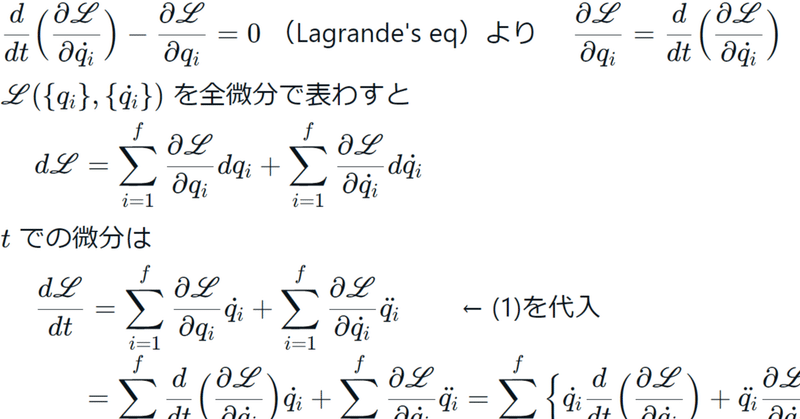
力学的エネルギー保存の法則
いくつかの方法で導く。
1 ニュートンの第2法則から
Newton's 2nd Low $${F(x)=m\ddot{x}}$$ ($${F=F(x)}$$とする)
両辺×$${\dfrac{dx}{dt}}$$
$${\dfrac{dx}{dt}F(x)=\dfrac{dx}{dt}m\ddot{x}}$$
$${\dfrac{dx}{dt}\Big(\dfrac{d}{dx}\displaystyle\int_0^x F(x)dx\Big)=m\dot{x}\dfrac{d\dot{x}}{dt}}$$
↑ 積分して微分するので元に戻る
$${\dfrac{d}{dx}\displaystyle\int_0^x F(x)dx=\dfrac{d}{dt}\Big(\dfrac{1}{2}m\dot{x}^2\Big)}$$
よって
$${\dfrac{d}{dx}\Big(\dfrac{1}{2}m\dot{x}^2-\displaystyle\int_0^x F(x)dx\Big)=0}$$
積分すると
$${\dfrac{1}{2}m\dot{x}^2-\displaystyle\int_0^x F(x)dx=\bm{const}}$$
$${\dfrac{1}{2}m\dot{x}^2+\Big(-\displaystyle\int_0^x F(x)dx\Big)=\bm{const}}$$
$${\dfrac{1}{2}m\dot{x}^2=T}$$、$${-\displaystyle\int_0^x F(x)dx=U}$$を代入すると $${T+U=\bm{const}}$$
2 保存力から
保存力$${\displaystyle\sum_{j=1}^nF_i=\displaystyle\sum_{j=i}^n\Big(-\dfrac{\partial U}{\partial x_i}\Big)}$$
$${\displaystyle\sum_{j=1}^nm_j\ddot{x_j}=\displaystyle\sum_{j=i}^n\Big(-\dfrac{\partial U}{\partial x_i}\Big)}$$ ← $${F_i=m_i\ddot{x_j}}$$
両辺×$${\dot{x_j}}$$
$${\displaystyle\sum_{j=1}^nm_j\ddot{x_j}\dot{x_j}=\displaystyle\sum_{j=i}^n\Big(-\dfrac{\partial U}{\partial x_i}\dot{x_j}\Big)}$$
$${\displaystyle\sum_{j=1}^n\dfrac{d}{dt}\Big(\dfrac{1}{2}m_j\dot{x_j}^2\Big)=\displaystyle\sum_{j=i}^n\Big(-\dfrac{\partial U}{\partial x_i}\dfrac{dx_j}{dt}\Big)}$$
$${\dfrac{d}{dt}\displaystyle\sum_{j=1}^n\Big(\dfrac{1}{2}m_j\dot{x_j}^2\Big)=\dfrac{1}{dt}\displaystyle\sum_{j=i}^n\Big(-\dfrac{\partial U}{\partial x_i}dx_j\Big)}$$
$${\dfrac{d}{dt}T=-\dfrac{d}{dt}U}$$
$${\dfrac{d}{dt}(T+U)=0}$$ 積分すると $${T+U=\bm{const}}$$
3 Lagrangeの運動方程式から
$${\dfrac{d}{dt}\Big(\dfrac{\partial\mathscr{L}}{\partial \dot{q_i}}\Big)-\dfrac{\partial\mathscr{L}}{\partial q_i}=0}$$(Lagrande's eq)より $${\dfrac{\partial\mathscr{L}}{\partial q_i}=\dfrac{d}{dt}\Big(\dfrac{\partial\mathscr{L}}{\partial \dot{q_i}}\Big)}$$ (1)
$${\mathscr{L}(\{q_i\},\{\dot{q_i}\})}$$を全微分で表わすと
$${d\mathscr{L}=\displaystyle\sum_{i=1}^f\dfrac{\partial\mathscr{L}}{\partial q_i}dq_i+\displaystyle\sum_{i=1}^f\dfrac{\partial\mathscr{L}}{\partial\dot{q_i}}d\dot{q_i}}$$
$${t}$$での微分は
$${\dfrac{d\mathscr{L}}{dt}=\displaystyle\sum_{i=1}^f\dfrac{\partial\mathscr{L}}{\partial q_i}\dot{q_i}+\displaystyle\sum_{i=1}^f\dfrac{\partial\mathscr{L}}{\partial\dot{q_i}}\ddot{q_i}}$$ ← (1)を代入
$${=\displaystyle\sum_{i=1}^f\dfrac{d}{dt}\Big(\dfrac{\partial\mathscr{L}}{\partial\dot{q_i}} \Big)\dot{q_i}+\displaystyle\sum_{i=1}^f\dfrac{\partial\mathscr{L}}{\partial\dot{q_i}}\ddot{q_i}=\displaystyle\sum_{i=1}^f\Big\{\dot{q_i}\dfrac{d}{dt}\Big(\dfrac{\partial\mathscr{L}}{\partial\dot{q_i}} \Big)+\ddot{q_i}\dfrac{\partial\mathscr{L}}{\partial\dot{q_i}}\Big\}}$$
$${=\displaystyle\sum_{i=1}^f\dfrac{d}{dt}\Big(\dot{q_i}\dfrac{\partial\mathscr{L}}{\partial\dot{q_i}} \Big)=\dfrac{d}{dt}\Big(\displaystyle\sum_{i=1}^f\dot{q_i}\dfrac{\partial\mathscr{L}}{\partial\dot{q_i}} \Big)}$$
すなわち
$${\dfrac{d}{dt}\Big(\displaystyle\sum_{i=1}^f\dot{q_i}\dfrac{\partial\mathscr{L}}{\partial\dot{q_i}}-\mathscr{L} \Big)=0}$$
積分すると
$${\displaystyle\sum_{i=1}^f\dot{q_i}\dfrac{\partial\mathscr{L}}{\partial\dot{q_i}}-\mathscr{L}=\mathbf{const}}$$
$${左辺=\displaystyle\sum_{i=1}^f\dot{q_i}\dfrac{\partial\mathscr{L}}{\partial\dot{q_i}}-\mathscr{L}=\displaystyle\sum_{i=1}^f\dot{q_i}\dfrac{\partial(T-U)}{\partial\dot{q_i}}-(T-U)}$$
$${=\displaystyle\sum_{i=1}^f\dot{q_i}\Big(\dfrac{\partial T}{\partial\dot{q_i}}-\dfrac{\partial U}{\partial\dot{q_i}}\Big)-(T-U)}$$ ← $${\dfrac{\partial U}{\partial\dot{q_i}}=0}$$
$${=\displaystyle\sum_{i=1}^f\dot{q_i}\dfrac{\partial}{\partial\dot{q_i}}T-(T-U)=\displaystyle\sum_{i=1}^f\dot{q_i}\dfrac{\partial}{\partial\dot{q_i}}\displaystyle\sum_{i=1}^f\Big(\dfrac{1}{2}m_i\dot{q_i}^2\Big)-(T-U)}$$
$${=\displaystyle\sum_{i=1}^f\dot{q_i}m_i\dot{q_i}-(T-U)=\displaystyle\sum_{i=1}^fm_i\dot{q_i}^2-(T-U)}$$
$${=2\displaystyle\sum_{i=1}^f\Big(\dfrac{1}{2}m_i\dot{q_i}^2\Big)-(T-U)=2T-(T-U)=T+U}$$
よって $${T+U=\bm{const}}$$
この記事が気に入ったらサポートをしてみませんか?
