Euler の微分方程式とLagrange の運動方程式はそっくりである。
実は同じ原理に基づいている。
　$${\text{Euler's eq}：\dfrac{d}{dt}\Big(\dfrac{\partial F}{\partial y'}\Big)-\dfrac{\partial F}{\partial y}=0}$$
　$${\text{Lagrange's eq}：\dfrac{d}{dt}\Big(\dfrac{\partial \mathscr{L}}{\partial \dot{q_i}}\Big)-\dfrac{\partial \mathscr{L}}{\partial q_i}=0}$$

１ Euler の微分方程式の復習

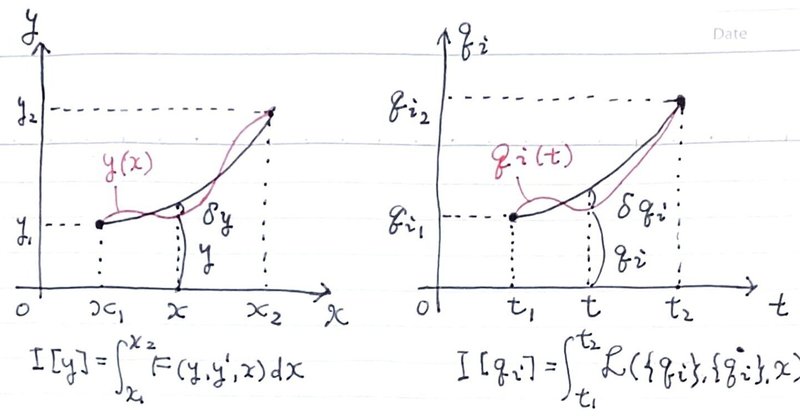
まず汎関数$${I[y]=\displaystyle\int_{x_1}^{x_2}F(y,  y', x)dx}$$を定義する。
汎関数が停滞値を取るためには
　$${\delta I[y]=\delta \displaystyle\int_{x_1}^{x_2}F(y,  y', x)dx=0}$$（変分原理）
この変分の式を変形、積分して導かれる式がEuler’s eq である。
　$${\dfrac{d}{dt}\Big(\dfrac{\partial F}{\partial y'}\Big)-\dfrac{\partial F}{\partial y}=0}$$
　（詳しい導出は https://note.com/greedyoldman/n/n72ac0b67498b ）

２ Lagrange's 運動方程式

$${q_i}$$軸､$${t}$$軸の座標系（右側）において $${t=t_1,  t=t_2}$$の両端の$${q_i(t)}$$を固定した区間内で考える。１と同様まず汎関数を定義するが、積分される関数は$${\mathscr{L(\{q_i\},\{\dot{q_i}\},t)}}$$である。
　$${I[\{q_i\}]=\displaystyle\int_{t_1}^{t_2}\mathscr{L}(\{q_i\},\{\dot{q_i}\},t)dt}$$　（この積分は作用積分ともいう）
この汎関数に変分原理$${\delta I[\{q_i\}]=0}$$（停滞値を取る条件）を使う。
これをHamiltonの原理という。（最小作用の原理ともいう）
　$${\delta I[\{q_i\}]=\delta\displaystyle\int_{t_1}^{t_2}\mathscr{L}(\{q_i\},\{\dot{q_i}\},t)dt}$$　　（$${t}$$は変化せず）
　　　$${=\displaystyle\int_{t_1}^{t_2}[\mathscr{L}(\{q_i+\delta q_i\},\{\dot{q_i}+\delta\dot{q_i}\},t)-\mathscr{L}(\{q_i\},\{\dot{q_i}\},t)]dt}$$
　　　　$${=\displaystyle\int_{t_1}^{t_2}\Big(\sum_{i=1}^f\dfrac{\partial\mathscr{L}}{\partial q_i}\delta q_i+\sum_{i=1}^f\dfrac{\partial\mathscr{L}}{\partial \dot{q_i}}\delta\dot{q_i}\Big)dt}$$
　　　$${=\displaystyle\sum_{i=1}^f\int_{t_1}^{t_2}\dfrac{\partial\mathscr{L}}{\partial q_i}\delta q_idt+\sum_{i=1}^f\int_{t_1}^{t_2}\dfrac{\partial\mathscr{L}}{\partial \dot{q_i}}\delta\dot{q_i}dt}$$（第2項を部分積分）
　　　$${=\displaystyle\sum_{i=1}^f\int_{t_1}^{t_2}\dfrac{\partial\mathscr{L}}{\partial q_i}\delta q_idt+\sum_{i=1}^f\Big\{\Big[\dfrac{\partial\mathscr{L}}{\partial \dot{q_i}}\delta{q_i}\Big]_{t_1}^{t_2}-\int_{t_1}^{t_2}\dfrac{d}{dt}\Big(\dfrac{\partial\mathscr{L}}{\partial \dot{q_i}}\Big)\delta{q_i}dt\Big\}}$$
　　　　　　　　　　　　　　（$${\delta q_i(t_1)=\delta q_i(t_2)=0}$$）
　　　$${=\displaystyle\sum_{i=1}^f\int_{t_1}^{t_2}\dfrac{\partial\mathscr{L}}{\partial q_i}\delta q_idt-\sum_{i=1}^f\int_{t_1}^{t_2}\dfrac{d}{dt}\Big(\dfrac{\partial\mathscr{L}}{\partial \dot{q_i}}\Big)\delta{q_i}dt}$$
　　　$${=\displaystyle\sum_{i=1}^f \int_{t_1}^{t_2}\Big\{\dfrac{\partial\mathscr{L}}{\partial q_i}-\dfrac{d}{dt}\Big(\dfrac{\partial\mathscr{L}}{\partial \dot{q_i}}\Big)\Big\}\delta{q_i}dt}$$
Hamiltonの原理 $${\delta I=0}$$より
　$${\delta I=\displaystyle\sum_{i=1}^f \int_{t_1}^{t_2}\Big\{\dfrac{\partial\mathscr{L}}{\partial q_i}-\dfrac{d}{dt}\Big(\dfrac{\partial\mathscr{L}}{\partial \dot{q_i}}\Big)\Big\}\delta{q_i}dt=0}$$
任意の$${\delta q_i}$$に対して成り立つためには
　$${\dfrac{\partial\mathscr{L}}{\partial q_i}-\dfrac{d}{dt}\Big(\dfrac{\partial\mathscr{L}}{\partial \dot{q_i}}\Big)=0}$$
書き直して
　$${\dfrac{d}{dt}\Big(\dfrac{\partial \mathscr{L}}{\partial \dot{q_i}}\Big)-\dfrac{\partial \mathscr{L}}{\partial q_i}=0}$$
この式は Euler-Lagrage's eq ともいう。