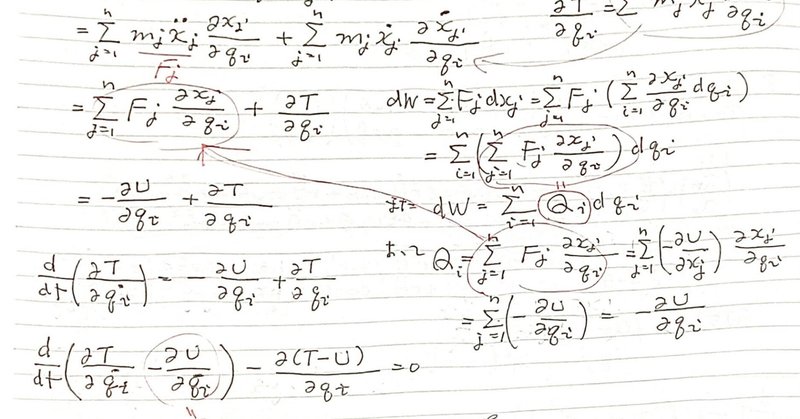
Lagrangeの運動方程式の導出
他に色気を出してしばらく遠ざかっていて久しぶりに復習したらすっかり忘れていた。Lagrangeの運動方程式の最後の導出は書いた時は理解していたのだろうが、端折った部分が今のわたしには意味不明である。若い頃に学習した内容は錆を簡単に落とせるが、歳を取ってからのものは朽ちるのが早い。弛緩し切った脳味噌で読んでもすぐにわかる様に今度はクソ丁寧に書くことにする。
1 デカルト座標と一般化座標
デカルト座標を$${x_1,x_2, … ,x_n=\{x_j\}}$$、一般化座標を$${q_1,q_2, … ,q_n=\{q_j\}}$$ とすると
$${x_1=x_1(q_1,q-2, … ,q_n)=x_1(\{q_i\})}$$
$${x_2=x_1(q_1,q_2, … ,q_n)=x_1(\{q_i\})}$$
・・・・・・・
$${x_j=x_j(q_1,q_2, … ,q_n)=x_j(\{q_i\})}$$ (1)
・・・・・・・
$${x_n=x_n(q_1,q_2, … ,q_n)=x_n(\{q_i\})}$$
例えば、座標$${x,y,z}$$と球座標$${r,θ,φ}$$なら以下の通り
$${x=r\sinθ\cosφ}$$、$${y=r\sinθ\sinφ}$$、$${z=r\cosθ}$$
2 加速度
(1) $${x_j=x_j(q_1,q_2, … ,q_n)=x_1(\{q_i\})}$$ より
$${\dot{x_j}=\dot{x_j}(q_1,q_2, .. ,q_n,\dot{q_1},\dot{q_2}, .. ,\dot{q_n})=x_j(\{q_i\},\{\dot{q_i\}})}$$
※ $${\dot{x_j}=x_j(\{\dot{q_i\}})}$$ ではない(1の球座標の例を参照)
Newton's eq
$${F_j=m_j\ddot{x_j}}$$ (2)
3 偏微分
(1) $${x_j=x_j(q_1,q_2, … ,q_n) より
全微分$${dx_j}$$は
$${dx_j=\dfrac{\partial x_j}{\partial q_1}dq_1+\dfrac{\partial x_j}{\partial q_2}dq_2+ … +\dfrac{\partial x_j}{\partial q_i}dq_i+ … +\dfrac{\partial x_i}{\partial q_n}dq_n}$$ (3)
$${t}$$で微分すると
$${\dfrac{dx_j}{dt}=\dfrac{\partial x_j}{\partial q_1}\dfrac{dq_1}{dt}+\dfrac{\partial x_j}{\partial q_2}\dfrac{dq_2}{dt}+…+\dfrac{\partial x_j}{\partial q_i}\dfrac{dq_i}{dt}+…+\dfrac{\partial x_j}{\partial q_n}\dfrac{dq_n}{dt}}$$
つまり
$${\dot{x_j}=\dfrac{\partial x_j}{\partial q_1}\dot{q_1}+\dfrac{\partial x_j}{\partial q_2}\dot{q_2}+…+\dfrac{\partial x_j}{\partial q_i}\dot{q_i}+…+\dfrac{\partial x_j}{\partial q_n}\dot{q_n}}$$
$${\dot{q_i}}$$で偏微分すると
$${\dfrac{\partial \dot{x_j}}{\partial \dot{q_i}}=\dfrac{\partial {x_j}}{\partial q_i} }$$ (4)
4 運動エネルギー
$${T=T(\dot{x_1},\dot{x_2},…,\dot{x_n})}$$ より
全微分$${dT}$$は
$${dT=\dfrac{\partial T}{\partial{\dot{x_1}}}d\dot{x_1}+\dfrac{\partial T}{\partial{\dot{x_2}}}d\dot{x_2}+ … +\dfrac{\partial T}{\partial{\dot{x_n}}}d\dot{x_n}}$$
$${T(\{\dot{x_j} \})}$$も$${\dot{x_j}(\{q_i \})}$$も多変数関数なので
$${{q_i}}$$で偏微分すると
$${\dfrac{\partial T}{\partial{q_i}}=\dfrac{\partial T}{\partial{\dot{x_1}}}\dfrac{\partial \dot{x_1}}{\partial{q_i}}+\dfrac{\partial T}{\partial{\dot{x_2}}}\dfrac{\partial \dot{x_2}}{\partial{q_i}}+ … +\dfrac{\partial T}{\partial{\dot{x_n}}}\dfrac{\partial \dot{x_n}}{\partial{q_i}}}$$
$${=\dfrac{\partial}{\partial{\dot{x_1}}}\Big(\dfrac{1}{2}m_1 \dot{x_1}^2\Big)\dfrac{\partial \dot{x_1}}{\partial{q_i}}+\dfrac{\partial}{\partial{\dot{x_2}}}\Big(\dfrac{1}{2}m_2 \dot{x_2}^2\Big)\dfrac{\partial \dot{x_2}}{\partial{q_i}}+ }$$
$${… +\dfrac{\partial}{\partial{\dot{x_n}}}\Big(\dfrac{1}{2}m_n \dot{x_n}^2\Big)\dfrac{\partial \dot{x_n}}{\partial{q_i}}}$$
$${=m_1 \dot{x_1}\dfrac{\partial \dot{x_1}}{\partial{q_i}}+m_2 \dot{x_2}\dfrac{\partial \dot{x_2}}{\partial{q_i}}+ … +m_n \dot{x_n}\dfrac{\partial \dot{x_n}}{\partial{q_i}}}$$
$${=\displaystyle\sum_{j=1}^n m_j \dot{x_j}\dfrac{\partial \dot{x_j}}{\partial{q_i}}}$$ (5)
$${\dot{q_i}}$$で偏微分すると
$${\dfrac{\partial T}{\partial \dot{q_i}}=\dfrac{\partial T}{\partial{\dot{x_1}}}\dfrac{\partial \dot{x_1}}{\partial \dot{q_i}}+\dfrac{\partial T}{\partial{\dot{x_2}}}\dfrac{\partial \dot{x_2}}{\partial \dot{q_i}}+ … +\dfrac{\partial T}{\partial{\dot{x_n}}}\dfrac{\partial \dot{x_n}}{\partial \dot{q_i}}}$$
$${=\dfrac{\partial}{\partial{\dot{x_1}}}\Big(\dfrac{1}{2}m_1 \dot{x_1}^2\Big)\dfrac{\partial \dot{x_1}}{\partial \dot{q_i}}+\dfrac{\partial}{\partial{\dot{x_2}}}\Big(\dfrac{1}{2}m_2 \dot{x_2}^2\Big)\dfrac{\partial \dot{x_2}}{\partial \dot{q_i}}+ }$$
$${… +\dfrac{\partial}{\partial{\dot{x_n}}}\Big(\dfrac{1}{2}m_n \dot{x_n}^2\Big)\dfrac{\partial \dot{x_n}}{\partial \dot{q_i}}}$$
$${=m_1 \dot{x_1}\dfrac{\partial \dot{x_1}}{\partial \dot{q_i}}+m_2 \dot{x_2}\dfrac{\partial \dot{x_2}}{\partial \dot{q_i}}+ … +m_n \dot{x_n}\dfrac{\partial \dot{x_n}}{\partial \dot{q_i}}}$$
$${=\displaystyle\sum_{j=1}^n m_j \dot{x_j}\dfrac{\partial \dot{x_j}}{\partial \dot{q_i}}}$$ (6)
5 ポテンシャル
$${U=U(x_1,x_2,…,,x_n)}$$ より
全微分$${dU}$$は
$${dU=\dfrac{\partial U}{\partial{{x_1}}}d{x_1}+\dfrac{\partial U}{\partial{{x_2}}}d{x_2}+ … +\dfrac{\partial U}{\partial{{x_n}}}d{x_n}}$$
$${U(\{{x_j} \})}$$も$${{x_j}(\{q_i \})}$$も多変数関数なので
$${\dfrac{\partial U}{\partial {q_i}}=\dfrac{\partial U}{\partial{{x_1}}}\dfrac{\partial {x_1}}{\partial {q_i}}+\dfrac{\partial T}{\partial{{x_2}}}\dfrac{\partial {x_2}}{\partial{q_i}}+ … +\dfrac{\partial T}{\partial{{x_n}}}\dfrac{\partial{x_n}}{\partial{q_i}}}$$$${=\displaystyle\sum_{i=1}^n\dfrac{\partial U}{\partial{{x_j}}}\dfrac{\partial{x_j}}{\partial{q_i}}}$$ (7)
6 保存力
保存力とは、その力のみが質点$${P}$$に作用して点$${P_1}$$から点$${P_2}$$までなした仕事が、その経路によらず2点$${P_1}$$、$${P_2}$$におけるポテンシャルの差$${U_1-U_2}$$だけで決まる力をいう。
$${n}$$次元において保存力を$${F}$$とすると
$${F=[F_1,F_2,…,F_j,…,F_n]}$$
$${=\Big[-\dfrac{\partial U}{\partial x_1},-\dfrac{\partial U}{\partial x_2}, … ,-\dfrac{\partial U}{\partial x_j}, … ,-\dfrac{\partial U}{\partial x_n}\Big]}$$
よって
$${F_j=-\dfrac{\partial U}{\partial x_j}}$$ (8)
7 一般化力
ある質点系$${(m_1,m_2,…,m_n)}$$に働く微小仕事$${dW}$$を2通りで表わす。
デカルト座標において
$${F_j}$$を外力、$${dx_j}$$を微小変位として
$${dW=F_1dx_1+F_2dx_2+…+F_ndx_n=\displaystyle\sum_{j=1}^nF_jdx_j}$$ (a)
一般化座標において
$${Q_j}$$を外力(一般化力)、$${dq_j}$$を微小変位として
$${dW=Q_1dq_1+Q_2dq_2+…+Q_ndq_n=\displaystyle\sum_{j=1}^nQ_jdq_j}$$ (b)
ところで
(3)$${dx_j=\dfrac{\partial x_j}{\partial q_1}dq_1+\dfrac{\partial x_j}{\partial q_2}dq_2+ … +\dfrac{\partial x_j}{\partial q_i}dq_i+ … +\dfrac{\partial x_i}{\partial q_n}dq_n}$$
$${=\displaystyle\sum_{i=1}^n\dfrac{\partial x_j}{\partial q_i}dq_i}$$ である。
これを(a)の$${dx_j}$$に代入すると
$${dW=\displaystyle\sum_{j=1}^nF_j\Big(\displaystyle\sum_{i=1}^n\dfrac{\partial x_j}{\partial q_i}dq_i\Big)=\displaystyle\sum_{i=1}^n\Big(\displaystyle\sum_{j=1}^nF_j\dfrac{\partial x_j}{\partial q_i}\Big)dq_i}$$ (c)
(b)と(c)を比較して
$${Q_i=\displaystyle\sum_{j=1}^nF_j\dfrac{\partial x_j}{\partial q_i}}$$
$${=\displaystyle\sum_{j=1}^n\Big(-\dfrac{\partial U}{\partial x_j}\Big)\dfrac{\partial x_j}{\partial q_i}}$$$${=ー\displaystyle\sum_{j=1}^n\dfrac{\partial U}{\partial x_j}\dfrac{\partial x_j}{\partial q_i}}$$ $${\Big(}$$(8)$${F_j=-\dfrac{\partial U}{\partial x_j}}$$より$${\Big)}$$
$${=ー\dfrac{\partial U}{\partial {q_i}}}$$ (9) $${\Big(}$$(7)$${\dfrac{\partial U}{\partial {q_i}}=\displaystyle\sum_{i=1}^n\dfrac{\partial U}{\partial{{x_j}}}\dfrac{\partial{x_j}}{\partial{q_i}}}$$より$${\Big)}$$
8 一般化運動量からラグランジュの運動方程式へ
運動エネルギー$${T}$$を$${\dot{q_i}}$$で偏微分したものを一般化運動量$${p_i}$$と定義する。
$${p_i\equiv\dfrac{\partial T}{\partial \dot{q_i}}}$$
$${=\dfrac{\partial }{\partial \dot{q_i}}\displaystyle\sum_{j=1}^n\dfrac{1}{2}m_i\dot{x_j}^2=\displaystyle\sum_{j=1}^n\dfrac{\partial }{\partial \dot{q_i}}\Big(\dfrac{1}{2}m_i\dot{x_j}^2\Big)}$$
$${=\displaystyle\sum_{j=1}^n\dfrac{\partial }{\partial \dot{x_j}}\Big(\dfrac{1}{2}m_i\dot{x_j}^2\Big)\dfrac{\partial \dot{x_j}}{\partial \dot{q_i}}=\displaystyle\sum_{j=1}^nm_i\dot{x_j}\dfrac{\partial \dot{x_j}}{\partial \dot{q_i}}}$$ 以下(4)への変形
$${=\displaystyle\sum_{j=1}^nm_i\dot{x_j}\dfrac{\partial }{\partial \dot{q_i}}\Big(\dfrac{dx_j}{dt}\Big)=\displaystyle\sum_{j=1}^nm_i\dot{x_j}\dfrac{\partial }{\partial \dot{q_i}}\Big(\dfrac{1}{dt}dx_j\Big)}$$
$${=\displaystyle\sum_{j=1}^nm_i\dot{x_j}\dfrac{\partial }{\partial \dot{q_i}}\Big(\dfrac{1}{dt}\displaystyle\sum_{i=1}^n\dfrac{\partial x_j}{\partial q_i}dq_i\Big)=\displaystyle\sum_{j=1}^nm_i\dot{x_j}\dfrac{\partial }{\partial \dot{q_i}}\Big(\displaystyle\sum_{i=1}^n\dfrac{\partial x_j}{\partial q_i}\dfrac{dq_i}{dt}\Big)}$$
$${=\displaystyle\sum_{j=1}^nm_i\dot{x_j}\dfrac{\partial }{\partial \dot{q_i}}\Big(\displaystyle\sum_{i=1}^n\dfrac{\partial x_j}{\partial q_i}\dot{q_i}\Big)=\displaystyle\sum_{j=1}^nm_i\dot{x_j}\dfrac{\partial x_j}{\partial q_i}}$$
両辺を$${t}$$で微分すると
$${\dot{p_i}=\displaystyle\sum_{j=1}^n\Big({m_i\ddot{x_j}}\dfrac{\partial x_j}{\partial q_i}+m_i\dot{x_j}\dfrac{\partial \dot{x_j}}{\partial q_i}\Big)=\displaystyle\sum_{j=1}^nm_i\ddot{x_j}\dfrac{\partial x_j}{\partial q_i}+\displaystyle\sum_{j=1}^nm_i\dot{x_j}\dfrac{\partial \dot{x_j}}{\partial q_i}}$$
$${=\displaystyle\sum_{j=1}^nF_j\dfrac{\partial x_j}{\partial q_i}+\dfrac{\partial}{\partial q_i}\displaystyle\sum_{j=1}^n\Big(\dfrac{1}{2}m_i\dot{x_j}^2\Big)=\displaystyle\sum_{j=1}^n\Big(-\dfrac{\partial U}{\partial x_j}\dfrac{\partial x_j}{\partial q_i}\Big)+\dfrac{\partial}{\partial q_i}T}$$
$${=\displaystyle\sum_{j=1}^n\Big(-\dfrac{\partial U}{\partial q_i}\Big)+\dfrac{\partial T}{\partial q_i}=-\dfrac{\partial U}{\partial q_i}+\dfrac{\partial T}{\partial q_i}=\dfrac{\partial (T-U)}{\partial q_i}}$$
$${\dot{p_i}}$$を書き換えて
$${\dfrac{dp_i}{dt}=\dfrac{\partial {(T-U)}}{\partial {q_i}}}$$
ここで$${T-U=\mathscr{L}}$$とおいて
$${\dfrac{dp_1}{dt}=\dfrac{\partial {\mathscr{L}}}{\partial {q_i}}}$$
左辺に(c)$${p_i=\dfrac{\partial T}{\partial \dot{q_i}}}$$を代入すると
$${\dfrac{d}{dt}\Big(\dfrac{\partial T}{\partial \dot{q_i}}\Big)=\dfrac{\partial {\mathscr{L}}}{\partial {q_i}}}$$
$${U}$$は$${\dot{q_i}}$$を含まず$${{q_i}}$$のみの関数なので $${\dfrac{\partial U}{\partial \dot{q_i}}=0}$$ である。
よって上式は
$${\dfrac{d}{dt}\Big(\dfrac{\partial T}{\partial \dot{q_i}}-\dfrac{\partial U}{\partial \dot{q_i}}\Big)=\dfrac{\partial {\mathscr{L}}}{\partial {q_i}}}$$と書ける。
$${\dfrac{d}{dt}\Big(\dfrac{\partial(T-U)}{\partial \dot{q_i}}\Big)-\dfrac{\partial \mathscr{L}}{\partial{q_i}}=0}$$
すなわち
$${\dfrac{d}{dt}\Big(\dfrac{\partial\mathscr{L}}{\partial \dot{q_i}}\Big)-\dfrac{\partial \mathscr{L}}{\partial{q_i}}=0}$$
ここで一般化運動量を$${p_i\equiv\dfrac{\partial\mathscr{L}}{\partial\dot{q_i}}}$$と再定義する。
以上がラグランジュの運動方程式の導出である。やれやれ。

この記事が気に入ったらサポートをしてみませんか?
