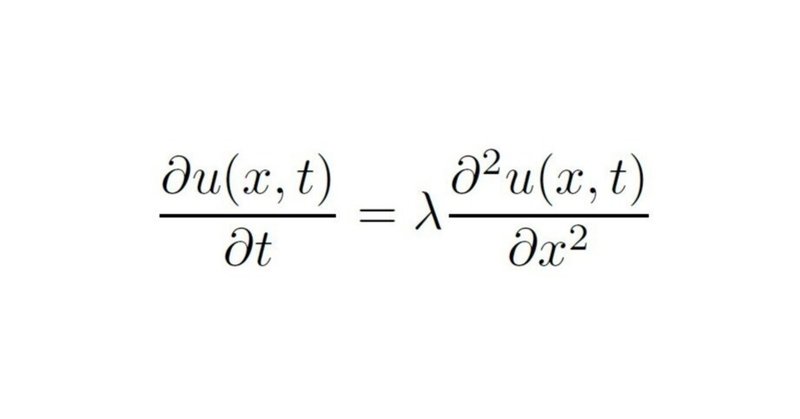
【偏微分方程式】1次元拡散方程式(無限区間)の解法
本記事では1次元拡散方程式(無限区間)の解析的な解法を示します。
有限区間の拡散方程式は別記事で扱っています。
※各種 偏微分方程式の解法一覧はこちら
前提知識:
線形代数
偏微分
常微分方程式(1階常微分方程式の解、境界条件、初期条件)
フーリエ変換の性質、畳み込み
以下の偏微分方程式を解く。
$$
\frac{{{\partial}}u(x, t)}{{{\partial}}t} = {\lambda}\frac{{{\partial}^2}u(x, t)}{{{\partial}}x^2} ({\lambda}:定数, t > 0)
$$
$$
u(x, 0) = u_0(x) (0 < x < 1, 初期条件)
$$
※$${u(x, t) = 0}$$は自明解なので考えない。
今回は無限区間なので境界条件がない。したがって、有限区間のときのように変数分離法で解くことはせず、代わりにフーリエ変換を用いる。
関数$${f(x)}$$のフーリエ変換は$${\mathscr{F}[f(x)]}$$で表すこととする。
1.$${u(x, t)}$$をフーリエ変換
$${u(x, t)}$$を$${x}$$についてフーリエ変換したものを$${U(\xi, t)}$$とする。すなわち
$$
U(\xi, t) = \mathscr{F}[u(x, t)]
$$
と表す。
拡散方程式の左辺$${{\partial}u(x, t)/{\partial}t}$$を$${x}$$についてフーリエ変換すると、$${t}$$はフーリエ変換に無関係なので
$$
\mathscr{F}[\frac{{\partial}u(x, t)}{{\partial}t}] = \frac{{\partial}}{{\partial}t}\mathscr{F}[u(x, t)] = \frac{{\partial}U(\xi, t)}{{\partial}t}
$$
となる。
一方で拡散方程式の右辺$${{\lambda}{{\partial}^2}u(x, t)/{{\partial}}x^2}$$を$${x}$$についてフーリエ変換すると
$$
\mathscr{F}[{\lambda}\frac{{{\partial}^2}u(x, t)}{{{\partial}}x^2}] = {\lambda}(i{\xi})^2\mathscr{F}[u(x, t)] = -{\lambda}{\xi}^2U(\xi, t)
$$
となる。
2.$${U(\xi, t)}$$を求める
以上のフーリエ変換により、拡散方程式は次のように変換できた。
$$
\frac{{{\partial}}u(x, t)}{{{\partial}}t} = {\lambda}\frac{{{\partial}^2}u(x, t)}{{{\partial}}x^2}
$$
$$
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,↓ (両辺をxについてフーリエ変換)
$$
$$
\frac{{\partial}U(\xi, t)}{{\partial}t} = -{\lambda}{\xi}^2U(\xi, t)
$$
$${U(\xi, t)}$$を$${t}$$の関数とみると、この式は$${t}$$に関する1階の常微分方程式とみなせる。
(分かりにくければ$${U(\xi, t) = {\Xi}(\xi)T(t)}$$と変数分離して式に当てはめれば確認できる。)
この常微分方程式の解は
$$
U(\xi, t) = U(\xi, 0)e^{-\lambda{\xi}^2t}
$$
となる。$${U(\xi, 0)}$$については
$$
U(\xi, 0) = \mathscr{F}[u(x, 0)] = \mathscr{F}[u_0(x)]
$$
であるので、まとめると
$$
U(\xi, t) = \mathscr{F}[u_0(x)]e^{-\lambda{\xi}^2t}
$$
となって$${U(\xi, t)}$$が求められた。
3.フーリエ逆変換で$${u(x, t)}$$を求める
$${U(\xi, t) = \mathscr{F}[u(x, t)]}$$より$${u(x, t) = \mathscr{F^{-1}}[U(\xi, t)]}$$が成り立つ。
したがって$${U(\xi, t)}$$をフーリエ逆変換して$${u(x, t)}$$が求められる。
$$
\mathscr{F^{-1}}[U(\xi, t)] = \mathscr{F^{-1}}[\mathscr{F}[u_0(x)]e^{-\lambda{\xi}^2t}]
$$
$$
= u_0(x) * \mathscr{F^{-1}}[e^{-\lambda{\xi}^2t}]
$$
$${*}$$は畳み込みを表す。
$${\mathscr{F^{-1}}[e^{-\lambda{\xi}^2t}]}$$はフーリエ変換表などを用いて
$$
\mathscr{F^{-1}}[e^{-\lambda{\xi}^2t}] =\frac{1}{2\sqrt{\pi\lambda{t}}}\exp({-\frac{x^2}{4\lambda{t}}})
$$
と求められる(別記事で証明する)ので、畳み込みによって
$$
u(x, t) = \mathscr{F^{-1}}[U(\xi, t)] = u_0(x) * \frac{1}{2\sqrt{\pi\lambda{t}}}\exp({-\frac{x^2}{4\lambda{t}}})
$$
$$
= \int_{-∞}^∞ u_0(y) \frac{1}{2\sqrt{\pi\lambda{t}}}\exp\{{-\frac{(x-y)^2}{4\lambda{t}}}\}\,dy
$$
となる。
以上により、解は次のようになる。
$$
u(x, t) = \int_{-∞}^∞ u_0(y) \frac{1}{2\sqrt{\pi\lambda{t}}}\exp\{{-\frac{(x-y)^2}{4\lambda{t}}}\}\,dy
$$
