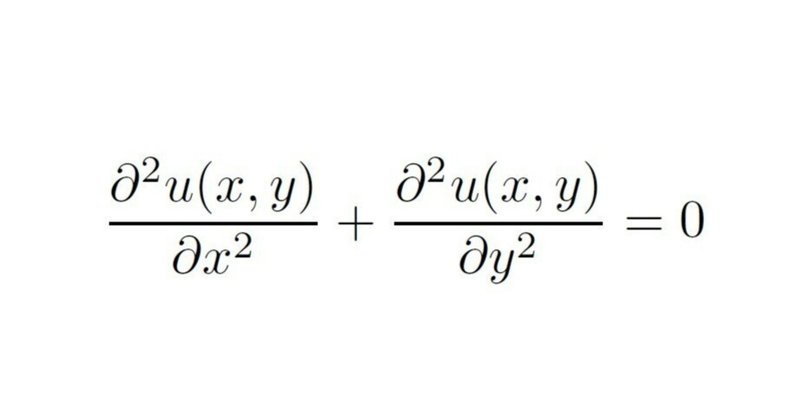
【偏微分方程式】2次元ラプラス方程式の解法
本記事では2次元ラプラス方程式の解析的な解法を示します。
※各種 偏微分方程式の解法一覧はこちら
前提知識:
線形代数
偏微分、双曲線関数
常微分方程式(2階常微分方程式の解、境界条件、初期条件)
簡単な複素関数($${e}$$の複素数乗)
三角関数の直交性(記事内でも簡単に解説します)
以下の偏微分方程式を解く。
$$
\frac{{{\partial}^2}u(x, y)}{{{\partial}}x^2} + \frac{{{\partial}^2}u(x, y)}{{{\partial}}y^2} = 0 (c:定数, 0 < x < 1, 0 < y < 1)
$$
$$
u(0, y) = u(1, y) = 0 (0 < y < 1, 境界条件)
$$
$$
u(x, 1) = 0 (0 < x < 1, 境界条件)
$$
$$
u(x, 0) = f(x) (0 < x < 1, 境界条件)
$$
※$${u(x, y) = 0}$$は自明解なので考えない。
1.変数分離
$${u(x, y) = X(x)Y(y) (X(x), Y(y) \neq 0)}$$ と表すと、ラプラス方程式は
$$
X''(x)Y(y) + X(x)Y''(y) = 0
$$
$$
\therefore \frac{X''(x)}{X(x)} = -\frac{Y''(y)}{Y(y)}
$$
と変形できる。
この式で、左辺の変数は$${x}$$のみ、右辺の変数は$${y}$$のみなので、等号が成り立つとき両辺は定数である。
定数を$${k}$$として
$$
\frac{X''(x)}{X(x)} = -\frac{Y''(y)}{Y(y)} = k
$$
2.$${X(x)}$$を求める
$${X(x)}$$について整理すると$${X''(x) = kX(x)}$$となる。
境界条件は
$$
u(0,y) = u(1, y) = 0
$$
より
$$
X(0)Y(y) = X(1)Y(y) = 0
$$
$$
\therefore X(0) = X(1) = 0
$$
となる。
定数$${k}$$が0の場合とそれ以外の場合に分けてこの常微分方程式を考える。
$${(1) k = 0}$$のとき
$${X''(x) = 0}$$より$${X(x) = ax+b}$$ ($${a,b}$$は定数)
境界条件を適用すると
$$
X(0) = b = 0
$$
$$
X(1) =a + b = 0
$$
これらを連立して解くと$${a = b = 0}$$となり$${X(x) = 0}$$を得る。
したがって$${k = 0}$$は不適。
$${(1) k \neq 0}$$のとき
$${X''(x) = kX(x)}$$の一般解は定数$${A, B}$$を用いて
$$
X(x) = Ae^{\sqrt{k}x} + Be^{-\sqrt{k}x}
$$
となる。境界条件を適用すると
$$
X(0) = A + B = 0
$$
$$
X(1) = Ae^{\sqrt{k}} + Be^{-\sqrt{k}} = 0
$$
これらを連立して解くと$${A, B}$$を得て$${X(x)}$$が求められるが、先にこの連立方程式が非自明解を持つ条件を確認する。
(非自明解を持たないとき$${X(x) = 0}$$となってしまう)
連立方程式$${A\bm{x} = \bm{0}}$$が非自明解を持つ必要十分条件は$${det(A) = 0}$$が成り立つことなので、
$$
e^{-\sqrt{k}}-e^{\sqrt{k}} = 0
$$
$$
\therefore e^{2\sqrt{k}} = 1
$$
$$
\therefore \sqrt{k} = n{\pi}i (n {\in} {\mathbb{Z}})
$$
したがって$${\sqrt{k} = n{\pi}i}$$すなわち$${k = -n^2{\pi}^2}$$のとき連立方程式は非自明解を持つ。
$${n}$$に対応する$${A, B}$$をそれぞれ$${A_n, B_n}$$と書き、これを用いた解$${X(x)}$$を$${X_n(x)}$$と書くこととすると
$$
X_n(x) = A_ne^{n{\pi}ix} + B_ne^{-n{\pi}ix}
$$
$$
= A_n(\cos{{n{\pi}x}} + i\sin{{n{\pi}x}}) + B_n(\cos{{n{\pi}x}} - i\sin{{n{\pi}x}})
$$
$$
= (A_n + B_n)\cos{n{\pi}x} + i(A_n-B_n)\sin{n{\pi}x}
$$
境界条件$${A_n + B_n = 0}$$より、$${i(A_n-B_n) = \alpha_n}$$とおいて
$$
X_n(x) = \alpha_n \sin{n{\pi}x}
$$
3.$${Y(y)}$$を求める
$${Y(y)}$$について整理すると$${Y''(y) = -kY(y)}$$となる。
$${Y(y)}$$の一般解は定数$${D, E}$$を用いて
$$
Y(y) = De^{\sqrt{-k}y} + Ee^{-\sqrt{-k}y}
$$
と表せる。
境界条件は
$$
u(x, 1) = 0
$$
より
$$
X(x)Y(1) = 0
$$
$$
\therefore Y(1) = 0
$$
なので、これを適用すると
$$
Y(1) = De^{\sqrt{-k}} + Ee^{-\sqrt{-k}} = 0
$$
ここから$${D}$$と$${E}$$の比が求められて
$$
\frac{E}{D} = -\frac{e^{\sqrt{-k}}}{e^{-\sqrt{-k}}}
$$
となる。そこで、$${D}$$と$${E}$$をそれぞれ次のように定める。
$$
D = -\frac{e^{-\sqrt{-k}}}{2}, E = \frac{e^{\sqrt{-k}}}{2}
$$
すると、$${Y(y)}$$は
$$
Y(y) = -\frac{e^{-\sqrt{-k}}}{2}e^{\sqrt{-k}y} + \frac{e^{\sqrt{-k}}}{2}e^{-\sqrt{-k}y}
$$
$$
= \frac{1}{2}(e^{\sqrt{-k}(1-y)} - e^{-\sqrt{-k}(1-y)})
$$
$$
= \sinh{\sqrt{-k}(1-y)}
$$
と変形できるので、$${X(x)}$$と同様に$${n}$$に対応する$${Y(y)}$$を$${Y_n(y)}$$とおいて
$$
Y_n(y) = \sinh{n{\pi}(1-y)}
$$
と求められる。
4.$${u(x, y)}$$の一般解を求める
したがって、$${X_n(x), Y_n(y)}$$を用いて表す解を$${u_n(x, y)}$$と書くと
$$
u_n(x, y) = X_n(x)Y_n(y)
$$
$$
= \alpha_n \sin{n{\pi}x}\,\sinh{n{\pi}(1-y)}
$$
と表せる。
この偏微分方程式は線形なので、解の線形結合も解になる。したがって
$$
\sum_{n = 1}^{\infin}u_n(x, y) = \sum_{n = 1}^{\infin}\alpha_n \sin{n{\pi}x}\,\sinh{n{\pi}(1-y)}
$$
も解である。これをこの偏微分方程式の一般解とし、$${u(x, y)}$$で表す。
$$
u(x, y) = \sum_{n = 1}^{\infin}\alpha_n \sin{n{\pi}x}\,\sinh{n{\pi}(1-y)}
$$
5.$${\alpha_n}$$を求める
境界条件
$$
u(x, 0) = \sum_{n = 1}^{\infin}\alpha_n \sin{n{\pi}x}\,\sinh{n{\pi}} = f(x)
$$
から$${\alpha_n}$$を求める。
両辺(中央と右)に$${\sin{m{\pi}x} (m \in \mathbb{N})}$$をかけると
$$
\sum_{n = 1}^{\infin}\alpha_n \sin{n{\pi}x}\,\sin{m{\pi}x}\,\sinh{n{\pi}} = f(x)\sin{m{\pi}x}
$$
となり、両辺を0から1まで$${x}$$について積分する。
三角関数の直交性(以下)により
$$
\int_0^1\sin{n{\pi}x}\sin{m{\pi}x}\,dx = \frac{\delta_{n,m}}{2}
$$
※$${\delta_{n,m}}$$はディラックのデルタ関数。
これを三角関数の直交性という。詳しくは「直交関数系」などで検索。
https://ja.wikipedia.org/wiki/%E7%9B%B4%E4%BA%A4%E9%96%A2%E6%95%B0%E5%88%97
$$
\int_0^1f(x)\sin{m{\pi}x}\,dx\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
$$
$$
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =\int_0^1\sum_{n = 1}^{\infin}\alpha_n \sin{n{\pi}x}\,\sin{m{\pi}x}\,\sinh{n{\pi}}\,dx = \frac{\alpha_m}{2}\sinh{m{\pi}}
$$
※$${n}$$は全ての自然数を順にとるので、必ず$${n = m}$$となる瞬間がある。このときに限り積分は$${{\alpha_m}\sinh{m{\pi}}/{2}}$$の値をとり、他では0となる。
よって、$${n}$$と$${m}$$を置き換えれば
$$
\alpha_n = \frac{2}{\sinh{n{\pi}}}\int_0^1f(x)\sin{n{\pi}x}\,dx
$$
というように$${\alpha_n}$$が求められた。
以上により、解は次のようになる。
$$
u(x, y) = \sum_{n = 1}^{\infin}\alpha_n \sin{n{\pi}x}\,\sinh{n{\pi}(1-y)}
$$
$$
\alpha_n = \frac{2}{\sinh{n{\pi}}}\int_0^1f(x)\sin{n{\pi}x}\,dx
$$
オマケ:境界条件$${u(x, 0) = f(x)}$$について
今回は$${(x, 0)}$$においてのみ関数$${f(x)}$$を用いて境界条件を定めたが、$${(x, 1)}$$や$${(0, y)}$$、$${(1, y)}$$でも同様に関数を用いて境界条件を定め、解を求める問題も考えられる。
すなわち
$$
\frac{{{\partial}^2}u(x, y)}{{{\partial}}x^2} + \frac{{{\partial}^2}u(x, y)}{{{\partial}}y^2} = 0 (c:定数, 0 < x < 1, 0 < y < 1)
$$
$$
u(x, 0) = f_1(x) (0 < x < 1, 境界条件)
$$
$$
u(x, 1) = f_2(x) (0 < x < 1, 境界条件)
$$
$$
u(0, y) = f_3(y) (0 < y < 1, 境界条件)
$$
$$
u(1, y) = f_4(y) (0 < y < 1, 境界条件)
$$
という問題も考えられる。しかし、4つの境界条件を同時に指定して解を求めることは難しい。
この問題を解くためには、今回のようにどれか1つだけを指定して他は0とする方法を用いる。
今回の解は$${f_1(x)}$$だけを指定したものだったが、同様に$${f_2(x)}$$から$${f_4(y)}$$だけを指定したときの解を求め、これらの解を足し合わせればこの問題の解となる。
