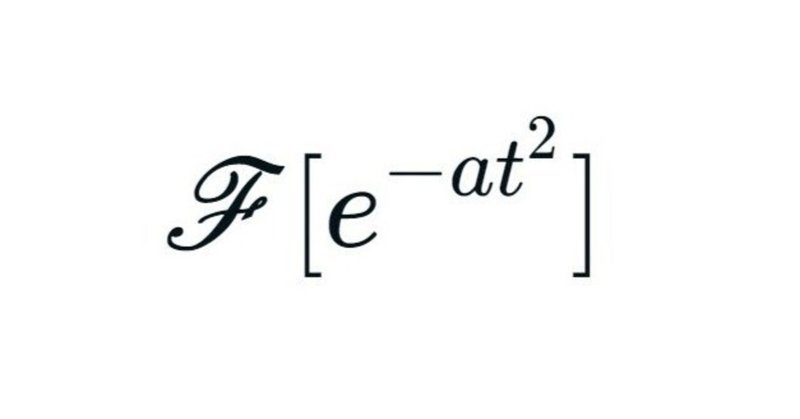
ガウス関数のフーリエ変換・逆変換
本記事ではガウス関数の一種である$${e^{-at^2}}$$のフーリエ変換および逆変換
$$
\mathscr{F}[e^{-at^2}] = \int_{-∞}^{∞}e^{-at^2}e^{-i{\xi}t}\,dt
$$
$$
\mathscr{F^{-1}}[e^{-a{\xi}^2}] = \frac{1}{2{\pi}}\int_{-∞}^{∞}e^{-a{\xi}^2}e^{i{\xi}t}\,d{\xi}
$$
を導出する。
前提知識:
微積
複素積分
フーリエ変換・逆変換
まずフーリエ変換を求める。
1.指数部を平方完成する
$$
\mathscr{F}[e^{-at^2}] = \int_{-∞}^{∞}e^{-at^2}e^{-i{\xi}t}\,dt = \int_{-∞}^{∞}e^{-at^2-i{\xi}t}\,dt
$$
$$
= \int_{-∞}^{∞}e^{{-a(t+\frac{i{\xi}}{2a})^2 - \frac{{\xi}^2}{4a}}}\,dt
$$
$$
= e^{- \frac{{\xi}^2}{4a}}\int_{-∞}^{∞}e^{{-a(t+\frac{i{\xi}}{2a})^2 }}\,dt
$$
2.複素積分を計算する
以下のような$${C_1~C_4}$$からなる経路$${C}$$を考える。
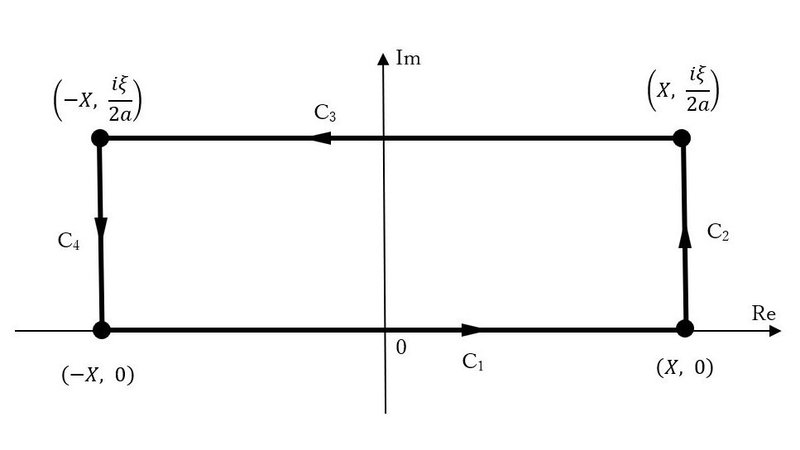
この経路に沿って$${e^{-az^2}}$$の周回積分を行うと
$$
0 = \oint_C e^{-az^2}\,dz
$$
$$
= \int_{-X}^{X} e^{-ax^2}\,dx + \int_{C_2}e^{-az^2}\,dz + \int_{X}^{-X} e^{(-a(x + \frac{i\xi}{2a})^2)}\,dx + \int_{C_4}e^{-az^2}\,dz
$$
となる。
ここで$${z = x + iy}$$と表すと
$$
|e^{-az^2}| = e^{Re(-az^2)} = e^{-a(x^2+y^2)} = e^{-ax^2}e^{-ay^2}
$$
であり、$${C_2}$$上では
$$
x = X, y ≦ \frac{\xi}{2a}
$$
であるので、
$$
|e^{-az^2}| = e^{-ax^2}e^{-ay^2} ≦ e^{-aX^2}e^{\frac{\xi}{2}}
$$
が成り立つ。
したがって、経路$${C_2}$$について
$$
|\int_{C_2}e^{-az^2}\,dz| ≦ \int_{C_2}|e^{-az^2}|\,|dz|
$$
$$
≦ \int_{C_2}|e^{-aX^2}e^{\frac{\xi}{2}}|\,|\frac{\xi}{2a}|\,dz \rightarrow 0 (X \rightarrow ∞)
$$
$$
\therefore \int_{C_2}e^{-az^2}\,dz \rightarrow 0 (X \rightarrow ∞)
$$
全く同様に
$$
\therefore \int_{C_4}e^{-az^2}\,dz \rightarrow 0 (X \rightarrow ∞)
$$
も成り立つ。したがって$${X \rightarrow ∞}$$のとき
$$
0 = \oint_C e^{-az^2}\,dz = \int_{-∞}^{∞} e^{-ax^2}\,dx + \int_{∞}^{-∞} e^{(-a(x + \frac{i\xi}{2a})^2)}\,dx
$$
$$
\therefore \int_{-∞}^{∞} e^{-ax^2}\,dx = \int_{-∞}^{∞} e^{(-a(x + \frac{i\xi}{2a})^2)}\,dx
$$
が成り立つことが示せた。
3.元のフーリエ変換に代入
1節で
$$
\mathscr{F}[e^{-at^2}] = \int_{-∞}^{∞}e^{-at^2}e^{-i{\xi}t}\,dt = e^{- \frac{{\xi}^2}{4a}}\int_{-∞}^{∞}e^{{-a(t+\frac{i{\xi}}{2a})^2 }}\,dt
$$
と変形したので、2節の結果を利用すると
$$
\mathscr{F}[e^{-at^2}] = e^{- \frac{{\xi}^2}{4a}}\int_{-∞}^{∞} e^{-at^2}\,dt
$$
とできる。
右辺の積分について、$${\sqrt{a}t = y}$$と変数変換すると
$$
\int_{-∞}^{∞} e^{-at^2}\,dt = \frac{1}{\sqrt{a}}\int_{-∞}^{∞} e^{-y^2}\,dy
$$
となり、右辺の積分は$${\sqrt{\pi}}$$であるので(簡単なガウス関数の積分なので証明略。)
$$
\int_{-∞}^{∞} e^{-at^2}\,dt = \sqrt{\frac{\pi}{a}}
$$
以上により、ガウス関数をフーリエ変換した値は次のようになる。
$$
\mathscr{F}[e^{-at^2}] = \sqrt{\frac{\pi}{a}}e^{- \frac{{\xi}^2}{4a}}
$$
ガウス関数のフーリエ逆変換は
$$
\mathscr{F^{-1}}[e^{-a{\xi}^2}] = \frac{1}{2{\pi}}\int_{-∞}^{∞}e^{-a{\xi}^2}e^{i{\xi}t}\,d{\xi}
$$
であるが、基本的にはフーリエ変換のときの計算と変わらない。
以下に略証明を示す。
指数部を平方完成して
$$
\mathscr{F^{-1}}[e^{-a{\xi}^2}] = \frac{1}{2{\pi}}\int_{-∞}^{∞}e^{-a{\xi}^2}e^{i{\xi}t}\,d{\xi} = = \frac{1}{2{\pi}}e^{- \frac{{t}^2}{4a}}\int_{-∞}^{∞}e^{-a({\xi}-\frac{it}{2a})^2}\,d{\xi}
$$
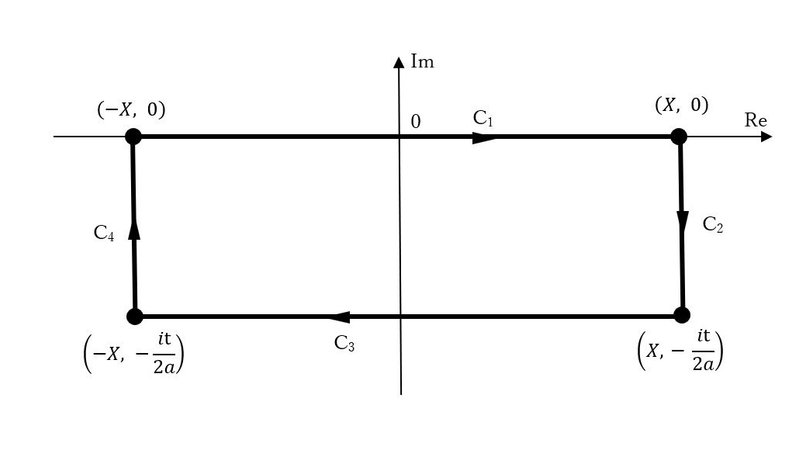
図のような$${C_1~C_4}$$からなる経路$${C}$$を考え、これに沿って$${e^{-az^2}}$$の周回積分を行う。
フーリエ変換のときと全く同様にして$${C_2, C_4}$$に沿った積分は$${X \rightarrow ∞}$$で0に収束するので
$$
\int_{-∞}^{∞} e^{-ax^2}\,dx = \int_{-∞}^{∞} e^{(-a(x - \frac{it}{2a})^2)}\,dx
$$
となる。したがって
$$
\mathscr{F^{-1}}[e^{-a{\xi}^2}] = \frac{1}{2{\pi}}e^{- \frac{{t}^2}{4a}}\int_{-∞}^{∞}e^{-a({\xi}-\frac{it}{2a})^2}\,d{\xi} = \frac{1}{2{\pi}}e^{- \frac{{t}^2}{4a}}\int_{-∞}^{∞} e^{-a{\xi}^2}\,d{\xi}
$$
が成り立ち、
$$
\int_{-∞}^{∞} e^{-a{\xi}^2}\,d{\xi} = \sqrt{\frac{\pi}{a}}
$$
であるので、ガウス関数のフーリエ逆変換の値は次のようになる。
$$
\mathscr{F^{-1}}[e^{-a{\xi}^2}] = \frac{1}{2{\pi}}\sqrt{\frac{\pi}{a}}e^{- \frac{{t}^2}{4a}} = \frac{1}{2\sqrt{a\pi}}e^{- \frac{{t}^2}{4a}}
$$
