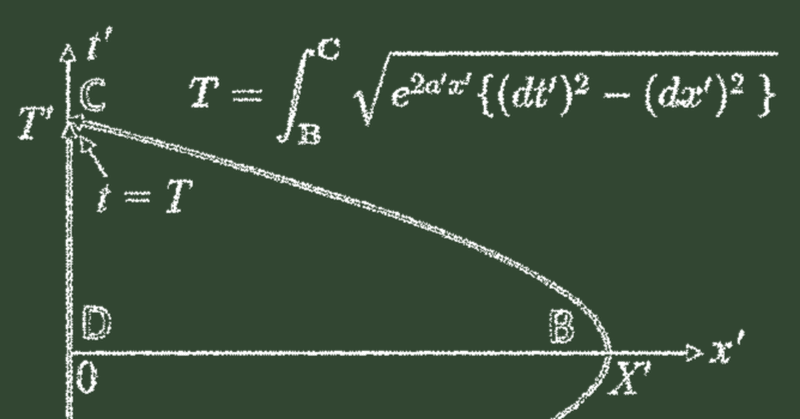
リンドラー座標系つれづれ(1)―双子のパラドックス―
はじめに
本稿でも、等加速度運動の相対論的な記述について紹介する。以下の記事の続きである。本稿の内容も、調べればどこかに解説されていることなので、自分のオリジナルな部分は特にない。表式を簡単にするため、前記事同様、以下で光速度$${c=1}$$とする単位系を使用する。
ざっと復習すると、静止系(S系)に対して、$${x}$$方向に一定の加速度$${a'}$$で動いている座標系をS'系とすると、S'系の座標$${(t', x')}$$とS系の座標$${(t, x)}$$の間の相対論的な変換式は、
$${\displaystyle t = \frac{1}{a'} e^{a'x'} \sinh a't'}$$ 式1
$${\displaystyle x = \frac{1}{a'} e^{a'x'} \cosh a't'}$$ 式2
で与えられる、というものである(リンドラ―変換)。今の場合、$${t = t' = 0}$$のとき、S'系の原点のS系における位置は、$${x = 1/a'}$$としている。図示すると、以下のようになる。$${x'}$$が一定の軌跡は、$${tx}$$空間では双曲線を描く。$${t'}$$が一定の軌跡は、すべて原点を通る直線となる。$${x' \to -\infty}$$あるいは$${t' \to\infty}$$のいずれの極限でも、光速度の軌跡$${t = x}$$の直線に収束する。
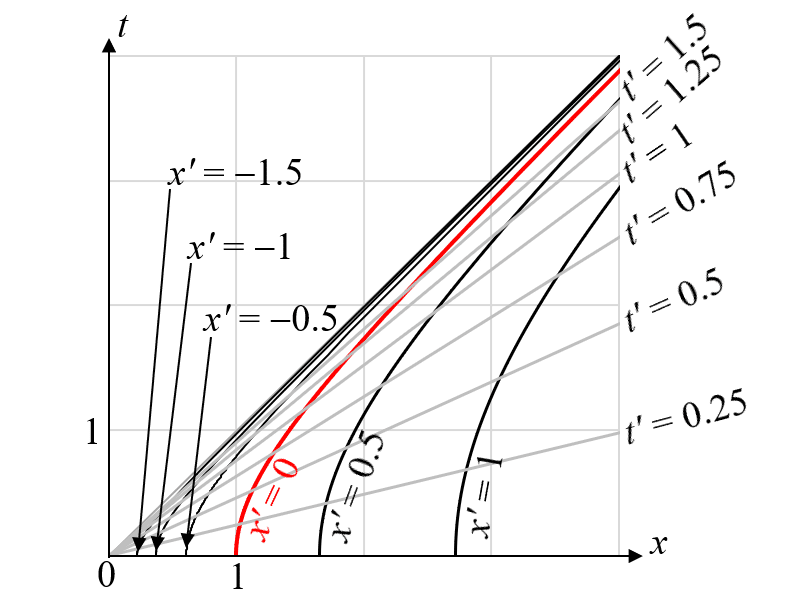
等速運動の場合のローレンツ変換とは違って、上図の通り非線形な変換となっているが、式1, 2の表式は非常に単純であり、以下に見るように種々の積分の厳密な計算も可能なので、いろいろと直観に反する帰結を導出して楽しむことができる。
双子のパラドックス
まず、このリンドラ―座標を用いて、有名な双子のパラドックスを解いてみよう。あまりにも有名な問題で、検索すれば簡単に解説が出てくるので、問題自体の詳細は割愛する。要は、
1) 静止系に対して、宇宙船か何かで遠くに行って戻ってくると、宇宙船に乗っている人間よりも、静止系に留まっていた人間の方が速く年をとってしまう(特殊相対論の帰結)。
2) 一方、宇宙船に乗っている人間から見れば、宇宙船が止まっていて、静止系の方が行って戻ってくるように見えるはず。この場合、宇宙船に乗っている人間の方が速く年をとることになるので、矛盾するのではないか?
という問題である。この問題は、(2)において、宇宙船に乗っている人間に対しても、(1)と同様に特殊相対論を適用しているところに誤りがある。宇宙船の方は行って戻ってくることになるので、どこかの時点で必ず加速度運動をする必要がある。特殊相対論は、観測者が慣性系にいることが前提になっているので、宇宙船に固定した座標系に特殊相対論を適用することはできず、重力を取り扱う一般相対論で議論する必要がある。加速度運動中は、宇宙船の中にいる人間は慣性力=重力を受け、それにより時間が遅れるため、(1)と同じ結果になる。
リンドラ―座標系で計算して、本当にそうなるか確認してみよう。静止系のある位置から、宇宙船が等加速度運動で出発して戻ってくる状況を考える。時空図で表すと、下図のようになる。

宇宙船の軌跡は赤線、静止系に留まる観測者の軌跡は青線である。出発点は$${t = -T}$$, $${x = X}$$で、宇宙船は加速度$${a'}$$の等加速度運動をして、時刻$${t = T}$$に最初の位置に戻る。このとき、宇宙船に乗った観測者が計る時刻は、$${t' = -T'}$$から$${t' = T'}$$となる。
静止系Sにいる観測者から見た場合
まず、静止系Sにいる観測者から見た場合を考える。宇宙船に乗った観測者が計る時刻$${T'}$$を求めるには、点DからCまで赤線に沿って以下の積分を計算すればよい(特殊相対論における固有時の計算)。
$${\displaystyle T' = \int_{\bold D}^{\bold C} \sqrt{(dt)^2-(dx)^2}}$$ 式3
が、、これの計算は前の記事で既に行っており、その結果としてリンドラ―変換の表式を得ているので、式1, 2をそのまま使えばよい。赤線上では$${x'=0}$$であるので、式1, 2より、
$${\displaystyle T = \frac{1}{a'} \sinh a'T'}$$ 式4
$${\displaystyle X = \frac{1}{a'} \cosh a'T'}$$ 式5
が成り立つ。式4より、
$${\displaystyle T' = \frac{1}{a'}\sinh^{-1}a'T}$$ 式6
となった。ここで、一般に逆双曲線関数$${\sinh^{-1}u}$$は$${u>0}$$のとき$${\sinh^{-1}u < u}$$であるから、$${T' < T}$$である。確かに静止系の方が時刻は進んでおり、特殊相対論から予想される通りである。
一様加速系S'にいる観測者から見た場合
次に、宇宙船に固定した座標系S'にいる観測者から見た場合を考える。そのためにまず、静止系Sにいる観測者の軌跡BC(上図の青線)を、S'系から見た場合の軌跡に直す必要がある。式2で$${x = X}$$として、$${x'}$$について解くと、
$${\displaystyle x' = \frac{1}{a'} \log\frac{a'X}{\cosh a't'} }$$ 式7
となり、これが宇宙船から見た場合の静止系観測者の軌跡となる。図示すると下図の青線のようになる。

宇宙線は赤線、静止系観測者は赤線
S’系では、静止系観測者は$${+x'}$$方向に進んで、また戻ってくるように見える。S’系から見た場合の、静止系観測者が図る時刻$${T}$$を求めよう。時刻$${T}$$を求めるには、点BからCまで青線に沿って以下の積分を計算すればよい(一般相対論における固有時の計算)。
$${\displaystyle T = \int_{\bold B}^{\bold C} \sqrt{-(ds')^2}}$$ 式8
ついに出てきた、泣く子も黙る一般相対論。S'系は慣性系ではないため、式3のようには計算できず、不変距離
$${\displaystyle (ds')^2 = g_{\mu\nu} dx'^\mu dx'^\nu}$$ 式9
を求める必要がある(慣性系の場合、計量テンソルが$${g_{\mu\nu} = \eta_{\mu\nu} = \text{diag}(-1,1) }$$となるので式3となる)。式1, 2を微分すると、
$${\displaystyle dt = (e^{2a'x'}\sinh a't')dx' + (e^{2a'x'}\cosh a't')dt'}$$ 式11
$${\displaystyle dx = (e^{2a'x'}\cosh a't')dx' + (e^{2a'x'}\sinh a't')dt'}$$ 式12
となる。不変距離は、S系とS’系で文字通り不変なので、
$${\displaystyle (ds')^2 = (ds)^2 = -(dt)^2+(dx)^2}$$
である。これに式11, 12を代入して少々計算すると、
$${\displaystyle (ds')^2 = e^{2a'x'}\{-(dt')^2+(dx')^2\}}$$ 式13
を得る。幸いにも非常に簡単な表式である。これを式8に代入して$${T}$$を求めよう。
$${\displaystyle T = \int_{\bold B}^{\bold C} \sqrt{e^{2a'x'}\{(dt')^2-(dx')^2\ \}} \\ \, \\ \quad = \int_0^{T'}e^{a'x'}\sqrt{1 - \left(\frac{dx'}{dt'}\right)^2} dt' }$$ 式14
ここで、式7より、$${\displaystyle dx' / dt' = -\tanh a't'}$$であるから、
$${\displaystyle T = \int_0^{T'}e^{a'x'}\sqrt{1-\tanh^2 a't'}dt' \\ \, \\ \quad = \int_0^{T'}\frac{e^{a'x'}dt'}{\cosh a't'}}$$
となる。さらに、式7より、$${\displaystyle e^{a'x'} = a'X / \cosh a't'}$$となるので、これを代入して、
$${\displaystyle T = a'X\int_0^{T'}\frac{dt'}{\cosh^2 a't'} \\ \, \\ \quad = X\tanh a'T'}$$ 式14
ここで、式5を代入して、
$${\displaystyle T = \frac{1}{a'}\sinh a'T'}$$ 式15
を得た。これは、静止系から見た場合に得た式6を、$${T}$$について解いた式に他ならない。当然$${T' < T}$$である。一般相対論を用いることにより、静止系から見た場合と同じ結果が得られた!
おわりに
余談ながら、自分で興味を持った問題に対して、能動的に一般相対論を適用して考えたのは今回が初めてだったので、よい復習になった。一般相対論は物理学科の4年次に授業で学んだのだが、相対性理論のうち、重力が絡む一般相対論は、宇宙物理や素粒子理論でも専攻しない限りほとんど使うことはないため、忘れてしまうものである(よく使う特殊相対論はそんなことないが)。双子のパラドックスの解法も、授業できちんと習った覚えがない。
リンドラ―座標に関する考察は長丁場になるので、今回は短いがここまでにしておく。次回は、この座標系で見た場合の物体の運動や、事象地平線について考える。
この記事が気に入ったらサポートをしてみませんか?
