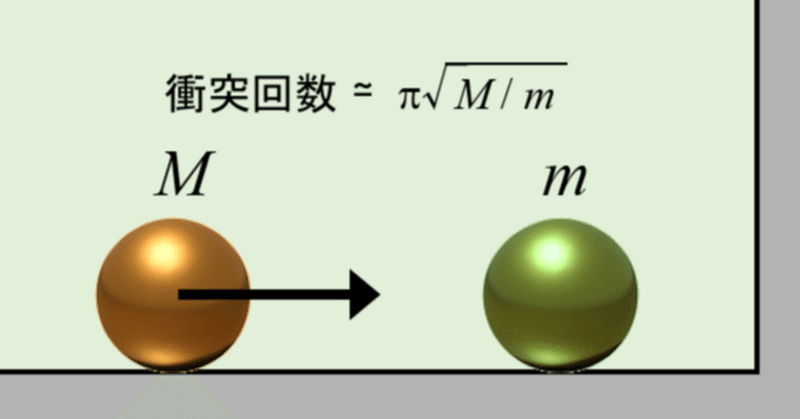
「ビリヤードπ計算機」の熱力学的解法
ビリヤードπ計算機とは、質量の異なる2つの玉を衝突させて、その衝突回数から円周率が求まるという力学的な装置のことである(私が勝手に命名)。
下図のように、水平面上に2つの玉M, m(それぞれ質量を$${M}$$, $${m}$$とし、$${M\ge m}$$)があり、玉Mを静止している玉mに向かって転がすと、玉Mの方が重いため、玉mは、玉Mと壁との間で衝突を繰り返す。
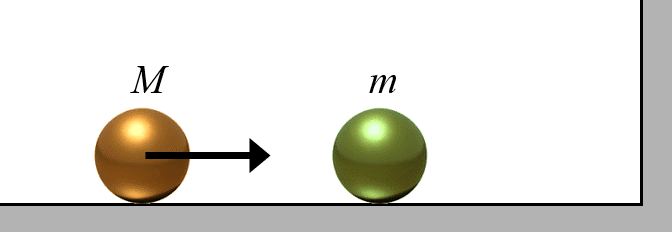
玉Mは、玉mに衝突される度に右向きの運動量を失い、やがて反転し、2つの玉は左向きに転がって、それ以上衝突しなくなる。この過程で、玉mが玉Mと壁に衝突する全回数を$${N}$$とすると、質量比$${M/m}$$が大きいほど$${N}$$も大きくなりそうなことは、直観的に分かるだろう。
で、$${N}$$は具体的にどう書けるか? 答えは、
$${\displaystyle N = \left[\pi\sqrt{\frac{M}{m}}\right]}$$ ・・式1
となる([ ]はガウス記号)。従って、質量比$${M/m}$$が$${100^n}$$ならば、衝突回数は円周率の先頭から$${n+1}$$ケタの数字になる、というものである。この性質は、$${M\ge m}$$を満たす任意の質量比で、かなり精密に成り立つ。
さて、式1はいかにして導出されるか?
1つの解法としては、エネルギーと運動量の保存則を用いて、上記衝突過程における玉mの運動量の推移を計算する方法である。元ネタの論文と、私がその解法に習って自分で計算した結果は下記記事に詳説した(非常に長い計算!)。
しかし、式1は非常にシンプルなため、例えば、$${M\gg m}$$の条件下では、何か別の方法でもっと簡単に求められそうである。
最近、熱力学に基づく別解をふと思い付き、あまり勝算のないまま何とか定式化して計算してみたら、全く同じ式を導出することができた。この問題の解法としてはほとんど知られてないし(オリジナル?)、物理的にも面白いと思われるので、紹介する。
気体の圧縮とのアナロジー
さて、玉mが玉Mと比して圧倒的に軽い$${M\gg m}$$の場合について、この問題を考える。2つの玉の運動量は、衝突を繰り返す度に離散的に変化するが、玉mが圧倒的に軽い場合、運動量の変化の刻みが小さくなるため、ほとんど連続的と見なせるだろう。この場合、上記の玉の衝突は、下図のようなピストンによる気体の圧縮と類似してくる。
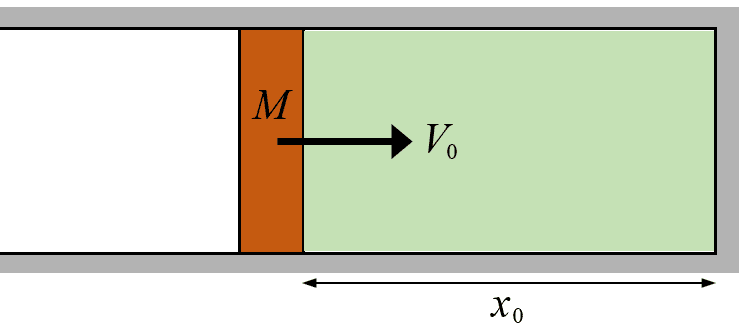
摩擦なしで自由に動くピストン(質量$${M}$$)があり、ピストンの右側には気体が封入されている。初期状態の気体の圧力は十分小さいとして、ピストンに右向きの初速度を与えると、気体は圧縮されて圧力が上がり、ある時点でピストンを押し返す。このとき、気体には外部からの熱の流入はないので、断熱過程となる。気体がピストンに及ぼす圧力は、ミクロで見れば、気体を構成する分子の衝突によって生じるため、質量$${m}$$の1分子で気体ができていると見なせば、上記ビリヤードの問題と同じとなる。それを敢えて粗視化して、気体の圧縮・膨張ととらえると、気体の断熱過程の保存量を与えるポワソンの法則を使えるため、ビリヤード問題をもっと簡単に解けそうである。
衝突回数の定式化
さて、玉mを気体と見なして、気体分子運動論に基づいて衝突回数を定式化しよう。気体分子は$${x}$$方向のみにしか動けない1次元の気体とする。圧縮・膨張の過程におけるピストンの位置(気体部分の長さ)を$${x}$$で表す。ピストン位置が$${x}$$のときの分子の速度を$${v}$$, 分子がピストン壁面に単位時間当たりに衝突する回数を$${n_t}$$とすると、分子は距離$${x}$$を往復する間に1回ピストンに衝突するので、
$${\displaystyle n_t = \frac{v}{2x}}$$・・式2
である。玉mの全衝突回数$${N}$$は、壁面との衝突もカウントするので、$${n_t}$$を2倍して、ピストンの圧縮・膨張の全過程において積分すればよい。
$${\displaystyle N = 2\int n_t dt = \int \frac{v}{x}dt}$$・・式3
ここで、時刻$${t}$$で積分するには、ピストンの運動が解けている($${x}$$が時刻$${t}$$の関数として得られている)必要があるが、一般に、運動を完全に解く必要がない場合、エネルギーや運動量の保存則によって得られやすい速度で表した方が都合がよい。なので、上式を以下のように$${x}$$の積分に置き換える。
$${\displaystyle N = \int \frac{v}{x}\frac{dt}{dx}dx=2\int_{x_1}^{x_0}\frac{v}{x}\frac{1}{V}dx}$$・・式4
ここで、$${x_0}$$は$${x}$$の初期値、$${x_1}$$は、ピストンが最も圧縮されたときの$${x}$$の最小値、$${V = dx/dt}$$はピストンの速度である。圧縮と膨張で運動が対称なため、さらに2倍の係数が掛かっていることに注意。以下で、$${v}$$, $${V}$$を$${x}$$の関数で表すため、熱力学的に議論する。
内部エネルギー
気体分子運動論に基づいて、気体の内部エネルギーの式を求めよう。今考えている気体は1分子から成り、分子はピストンと壁との衝突を繰り返している。運動量の$${mv}$$の1分子がピストン壁面に衝突して反転するときの運動量の変化は$${2mv}$$となる。気体がピストンに及ぼす力を$${F}$$とすると、運動量の変化=力積の関係
$${\displaystyle 2mv= F\Delta t}$$・・式5
が成り立つ。ここで、分子は、その時点における気体の長さ$${x}$$を1往復する間に1回ピストンに衝突するので、$${\Delta t=2x/v}$$となる。上式に代入して、
$${\displaystyle Fx = mv^2}$$・・式6
を得る。気体の内部エネルギー$${U}$$は分子の運動エネルギーであるので、上式を用いて、
$${\displaystyle U = \frac{1}{2}mv^2 = \frac{1}{2}Fx}$$・・式7
となる。
熱力学の第1法則の適用
気体は断熱過程であるので、内部エネルギーの変化は、外部からされる仕事に等しい。従って、熱力学の第1法則より、
$${dU = -Fdx}$$・・式8
となる(今の場合、圧縮されるときは$${dx < 0}$$で$${dU>0}$$)。式7を用いると、
$${\displaystyle dU = \frac{1}{2}(Fdx+xdF)}$$・・式9
となるため、式8, 9から、
$${\displaystyle 3Fdx + xdF = 0\\\,\\ 3\frac{dx}{x} + x\frac{dF}{F} = 0}$$
従って、保存量
$${\displaystyle Fx^3 = \text{const.}}$$・・式10
が得られた。これは、3次元気体の断熱過程のポワソンの法則に相当する。
種々の量を気体の長さで表す
次に、気体の内部エネルギーを、その時点の長さ$${x}$$のみで表す。そのために、保存量式10を用いる。式10の量が初期値から変わらないわけだが、初期値はいくらか? ここで、気体の初期状態として、分子の速度がゼロ、従って、ピストンを押す力も$${F = 0}$$とすると、式10の値もゼロになってしまうため都合が悪い。そこで、初期値は、最初に静止していた分子がピストンと最初の衝突をした直後の状態に基づいて設定する。
初速度$${V_0}$$のピストンが静止している気体分子に衝突した場合、衝突後の分子の速度は、エネルギーと運動量の保存則から、質量比$${\varepsilon \equiv m/M}$$を用いて、
$${\displaystyle v_0 = \frac{2}{1+\varepsilon}V_0}$$・・式11
となる。ここで、今の場合、$${\varepsilon \ll 1}$$であるので、
$${v_0 \simeq 2V_0}$$・・式12
と見なす。以下、これを用いると、内部エネルギーの初期値は、
$${\displaystyle U_0 = \frac{1}{2} F_0 x_0\simeq\frac{1}{2}mv_0^2 \\\,\\\quad\,\,=\frac{1}{2}m(2V_0)^2\\\,\\\quad\,\,=2mV_0^2}$$・・式13
であるため、
$${\displaystyle F_0 x_0 = 4mV_0^2}$$・・式14
を得る。これを用いると、式10の保存量は、
$${\displaystyle Fx^3 = F_0 x_0^3 = 4mV_0^2 x_0^2}$$・・式15
となる。さらに、これを用いて、任意の長さ$${x}$$のときの内部エネルギーは、
$${\displaystyle U = \frac{1}{2}Fx = 2mV_0^2 \frac{x_0^2}{x^2} }$$・・式16
となる。また、$${U = (1/2)mv^2}$$であるから、
$${\displaystyle v = 2V_0 \frac{x_0}{x}}$$・・式17
を得る。
ピストンの速度
次に、任意の長さ$${x}$$のときのピストンの速度$${V}$$を求める。エネルギー保存則により、
$${\displaystyle \frac{1}{2}MV^2 +U= \frac{1}{2}MV_0^2 +U_0}$$・・式18
となる。式13, 16を代入して解くと、
$${\displaystyle V = V_0\left\{ 1 -\frac{4m}{M} \left(\frac{x_0^2}{x^2} - 1\right)\right\}}$$・・式19
が得られる。さらに、気体が最圧縮されたときの長さ$${x_1}$$は、上式を$${V = 0}$$として$${x}$$について解いて、
$${\displaystyle x_1 = \zeta x_0,\\\quad\,\, \zeta\equiv \sqrt{\frac{4\varepsilon}{1+4\varepsilon}},\,\,\varepsilon \equiv \frac{m}{M}}$$・・式20
となる。
積分の計算
以上で材料が揃ったので、式4の積分を実行しよう。果たして厳密に解ける形になってくれるか、緊張の一瞬である。式4に式17, 19, 20を代入して、
$${\displaystyle N = 2\int_{\zeta x_0}^{x_0} \frac{2V_0 x_0}{x^2}\frac{1}{V_0\sqrt{1 - \frac{4m}{M}\left(\frac{x_0^2}{x^2}-1 \right)}}dx\\\,\\\quad\, =4x_0\int_{\zeta x_0}^{x_0}\frac{dx}{x^2\sqrt{1 - \frac{4m}{M}\left(\frac{x_0^2}{x^2}-1 \right)}}\\\,\\\quad\, = 4\int_{\zeta x_0}^{x_0}\frac{dx}{x\sqrt{(\frac{x}{x_0})^2-4\varepsilon\left\{1 - (\frac{x}{x_0})^2 \right\}}}}$$・・式21
ここで、$${y \equiv x/x_0}$$と置くと、
$${\displaystyle N = 4\int_\zeta^1\frac{dy}{y\sqrt{y^2-4\varepsilon(1-y^2)}}\\\,\\\quad\,=\frac{4}{\sqrt{1+4\varepsilon}}\int_\zeta^1\frac{dy}{y\sqrt{y^2-\zeta^2}}}$$・・式22
さらに、$${y \equiv \zeta z}$$と置くと、
$${\displaystyle N = \frac{2}{\sqrt{\varepsilon}}\int_1^{1/\zeta}\frac{dz}{z\sqrt{z^2-1}}}$$・・式23
となる。だいぶ簡単な表式になった。分母の根号を外したい。こういう場合、とりあえず根号自体を別の変数に置換するのが王道である。$${u = \sqrt{z^2-1}}$$と置くと、
$${\displaystyle du = \frac{z}{\sqrt{z^2-1}}dz}$$・・式24
となるので、式23に代入すると、うまく根号がキャンセルして、さらに、$${z = 1 + u^2}$$であるので、
$${\displaystyle N = \frac{2}{\sqrt{\varepsilon}}\int_{0}^{\frac{1}{2\sqrt{\varepsilon}}}\frac{du}{1+u^2}}$$・・式25
となる。この形になると、もはや$${u = \tan\theta}$$と置けば簡単に積分できる。
$${\displaystyle \frac{1}{1+u^2}=\cos^2\theta,\,\,du = \frac{d\theta}{\cos^2\theta}}$$
であるから、式25は、
$${\displaystyle N = \frac{2}{\sqrt{\varepsilon}}\int_0^{\arctan\frac{1}{2\sqrt{\varepsilon}}}du \\\,\\\quad\,= \frac{2}{\sqrt\varepsilon}\arctan\frac{1}{2\sqrt{\varepsilon}}}$$・・式26
と積分できた。ここで、今の場合、$${\varepsilon = m/M \ll 1}$$であるから、$${\arctan(1/2\sqrt{\varepsilon})\simeq \pi/2}$$と近似できる。従って、式26は、
$${\displaystyle N \simeq \frac{\pi}{\sqrt{\varepsilon}}=\pi\sqrt{\frac{M}{m}}}$$・・式27
となり、冒頭の式1と同じ結果が得られた。お見事!
おわりに
以上、同じ力学的問題を、ミクロ視点で厳密に解いた場合と、マクロ視点で粗視化して解いた場合で、一致すべき量がきちんと一致したという話でした。元ネタ論文の厳密解法と比べて計算量は圧倒的に少なく、代わりに物理的な考察を多用しているのが今回の解法の特徴である。個人的に、何も参照せずに自分で解法を思い付いて、期待する結果を自力で導出できたのが良かった。国際物理オリンピックの問題にでも誘導形式で出題したら面白いかも、と思ったが、さすがにこれは大学レベルか。
この記事が気に入ったらサポートをしてみませんか?
