はじめに

　1990年に放送されたシリーズもののNHKスペシャル「銀河宇宙オデッセイ」を覚えている人がいたら、いい年した大人だろう。当時最先端の天文学の世界を紹介する科学番組なのだが、当時まだ珍しかったCGを駆使した映像が美しく、とにかくそのクオリティが半端なく高かったのをよく覚えている。当時中学2年の私は天文にハマっており、朝日文庫から出ていたカール・セーガンの「COSMOS」で読んだ世界が、当時最先端のCG映像で再現されているのを見て、心底感激したのだった。

この番組は、単に科学的内容を紹介するだけでなく、豪華セットと本物の俳優を使った劇中映画が挿入されていたのだが、個人的にこれがツボだったのである。宇宙船「ヘリオス」に乗って宇宙空間を旅するクルーたちが、毎回、その回の放送のテーマに沿った事件に遭遇するというストーリーで、ヘリオスのクルーは、国籍も様々な5人（うろ覚えだが、確か女性2人、男性3人で、船長は年配のアジア系女性）。うち1人が、俳優の別所哲也が演じる日本人という設定だった。クルーたちの会話は英語で、劇中は日本語字幕が付いていた。別所哲也の英語の発音がきれいで、何ともかっこよかった。「ヘリオス」のミッションはよく覚えてないが、船外活動中に高エネルギー宇宙線に危うく被曝しそうになったり、超新星爆発を間近で観測したり（今考えると荒唐無稽すぎ！）と、とにかく色々なことが起き、最後の方では、クルーの男女2人が恋仲になったりとかの人間模様もあった覚えがある。

で、放送何回目かの劇中映画で、ブラックホールに遭遇するシーンがあった。母船から離れて調査用の小型船に乗った2人が、宇宙空間のある方向に、背景の星が見えない真っ暗な円形の領域があるのを発見する。その黒い円形領域の縁に沿って、背景の星の景色が不自然に歪んで見える。「何だあれは？」とか言ってる間に、船がその方向に引き寄せされて、どんどん加速しているのに気づく。慌てて後退しようとするが、加速がさらに強くなり、2人の体には後ろ向きの強烈な力を受けて（車が前に加速するときと同じ）、体がシートにへばり付いてしまう。操縦桿に手を伸ばそうとしても、腕を前方に出すことすらままならない。クルーの1人が渾身の力を込めて操縦桿まで手を伸ばし、ギリギリのところで脱出できた、というシーンである。

俳優たちの迫真の演技も良かったし、ブラックホールの重力レンズ効果までCGで再現してたりして、一見良くできていたのだが、、、

この描写、物理的に間違っているのである。

乗り物が前方に加速すると、確かに、中にいる人は後方に慣性力を受けるのだが、このシーンの場合、引っ張る力はブラックホールの重力である。重力の場合、中にいる人間の体にも遠隔作用的に引力が働くため、慣性力と完全に打ち消し合って、加速中も上記のような後ろ向きの力を感じることはない。言わば、空気抵抗のない真空中をスカイダイビングしているようなものである。

長々と思い出話をしてしまったが、本稿では理論物理学の金字塔たる相対性理論に少しだけ触れる。上記のように、重力に引かれて自由落下している観測者は、自分が静止系にいる状況と原理的に区別できないというのは、アインシュタインが一般相対論の構築の土台とした等価原理のアイデアそのものである。ところで、相対論によると、質量を持つ物体の速度は光速度以上に達することは原理的にできないが、では、上記の宇宙船のように、一定加速度で運動し続ける場合、話はどうなるか？別件の問題（そのうち記事をアップ予定）を考えるに当たって、一定の加速度運動の相対論的な記述を理解する必要に迫られたため、理解を深めるために、学生時代に学んだ相対論を思い出しながら、座標の変換式を自力で導出しようとスキマ時間に考えた結果、1ヶ月ほどかかってようやく導出することができた。せっかくなので、考えた道筋をここに記録しておく（本稿の内容は、調べればどこかに書いてあることなので、私のオリジナルな部分は一切ありません）。

等速運動の場合

相対論を簡単な問題から復習する。以下で、表式を簡単にするために、光速度を$${c=1}$$とする単位系を用いることにする。静止系（S系）に対して、$${x}$$方向に一定の速度$${\beta}$$で動いている座標系をS'系とする。S'系の座標$${(t', x')}$$は、S系の座標$${(t, x)}$$でどう書けるか？答えは、ローレンツ変換

$${\displaystyle \begin{bmatrix}t'\\x'\end{bmatrix}= \begin{bmatrix}\gamma & -\gamma\beta\\-\gamma\beta & \gamma\end{bmatrix} \begin{bmatrix}t\\x\end{bmatrix}}$$　式1

となる。ここで、$${\gamma}$$はローレンツ因子$${\gamma=1/\sqrt{1-\beta^2}}$$である。逆変換は、

$${\displaystyle \begin{bmatrix}t\\x\end{bmatrix}= \begin{bmatrix}\gamma & \gamma\beta\\\gamma\beta & \gamma\end{bmatrix} \begin{bmatrix}t'\\x'\end{bmatrix}}$$　式2

である。この辺は特殊相対論の基本中の基本なので、さすがに覚えている。上記の変換は、以下のような時空図で書くと分かりやすい。

図中の$${\theta}$$は、$${\tan\theta = \beta}$$となる角度である。S系の基底の単位ベクトル$${\bold e_t}$$, $${\bold e_x}$$は、式2の変換によって、青矢印で示した$${\bold e_{t}'}$$, $${\bold e_{x}'}$$に写される。S'系では、この青字の$${\bold e_{t}'}$$, $${\bold e_{x}'}$$を単位ベクトルとして目盛りが刻まれる。この目盛りで測った値が、式1で表されるわけである（ローレンツ変換による基底ベクトル自体の変換行列と、基底ベクトルの変換による座標値の変換行列は、互いに逆行列になることに注意）。

この図を眺めると、いわゆる、速度による時間の遅れと長さの収縮の現象は直ちに理解できる。S'系の$${x' = 0}$$に固定されている時計の時空図上の軌跡は、$${t'}$$軸となる。その軸上の$${t' = 1}$$の点の時刻は、$${t}$$軸の目盛りで読むと$${\gamma}$$になるため、$${t' = t/\gamma}$$となり、静止系から見ると、S'系の時刻の進みは$${1/\gamma}$$倍に遅くなる。また、S'系に固定されている長さ1の線分（図1中の基底ベクトル$${\bold e_{x}'}$$そのもの）の時空図上の軌跡は、$${t'}$$軸と$${x'=1}$$の2直線に挟まれた帯となる。この帯を、S系の同時刻、すなわち、$${x}$$軸に平行な直線で切ると、その長さは$${1/\gamma}$$に収縮する（長さを測る場合は、それぞれの座標系で同時刻に両端の位置を測る必要があることに注意）。

等加速度運動の場合はどうなるか？

以上は等速運動の場合だが、等加速度運動の場合はどうなるか？S'系が初速度ゼロで一定の加速度で動く場合、静止系からみたS'系の時空図上の軌跡は、以下の図のような感じになることは想像が付く。

一定加速度で動き続けても、S系から見ると、その速度はいずれ光速度に収束し、加速度もゼロに収束するはずである。このとき、一様加速するS'系の座標軸の向きは、上図に示したように、各瞬間における速度$${\beta}$$に応じて変化していく。速度が増すほど基底ベクトル$${\bold e_{t}'}$$, $${\bold e_{x}'}$$は引き延ばされ、$${t'}$$及び$${x'}$$両軸の向きは$${t = x}$$の直線に漸近していく。

さて、この一様加速系S'と、静止系Sとの間の座標変換式を求めたい。そのために、まず、S'系に固定された観測者のS系における軌跡（上図の青い曲線）を求めることにする。さて、どう考えればよいか？ここでつまずいたのだが、しばらく考えて、以下のようなステップを踏めばよいと思い付いた。

1) S系に対してS'系が$${x}$$方向に速度$${\beta_1}$$で動いており、さらに、S'系にいる観測者が、S'系において$${x'}$$方向に速度$${\beta_2'}$$で動いている状況を考える。速度$${\beta_1}$$, $${\beta_2'}$$は一定でなくてよい。

2) S'系にいる観測者は、S'系において常に$${x'}$$方向に加速度$${a'}$$を持っており、かつ、S'系における速度は常に$${\beta_2'=0}$$とする。つまり、S'系自体が、加速度$${a'}$$で前進している宇宙船であり、観測者はその中で静止しているとみなす。

3) 上記の条件の下で$${\beta}$$を時刻$${t}$$の関数で表し、それを積分して$${x}$$を$${t}$$で表す。

速度の合成則

さて、上記ステップ(1)から考える。S'系で速度$${\beta'_2}$$で動いている観測者を、S系から見た場合の速度を$${\beta}$$とすると、$${\beta}$$は、$${\beta_1}$$と$${\beta'_2}$$を用いてどう書けるか？これは、特殊相対論で有名な速度の合成の問題である。せっかくなのでこれも導出してみる。定義から、$${\beta'_2 = dx' / dt'}$$である。今求めたいのは、S系の座標で表した速度$${\beta = dx / dt}$$である。式2を微分すると、

$${\displaystyle dt = \gamma dt' + \gamma \beta_1 dx' \\ \\ dx = \gamma \beta_1 dt' + \gamma dx' }$$

を得る。従って、

$${\displaystyle \beta =\frac{dx}{dt} =\frac{\beta_1 dt' + dx'}{dt' + \beta_1 dx'} \\ \, \\ \quad =\frac{\beta_1 + dx'/dt'}{1+\beta_1 dx'/dt'}\\ \, \\ \quad =\frac{\beta_1+\beta'_2}{1+\beta_1\beta'_2}}$$　式3

となって、速度の合成則の式が得れれた。

加速度の合成則

次に、上記ステップ(2)を考える。求めたいのは、S'系にいる観測者の加速度$${a'}$$と、それをS系で見たときの加速度$${a}$$との関係式である。定義より、$${a = d\beta/dt}$$, $${a' = d\beta'_2/dt'}$$である。式3を$${t}$$で微分しよう。今の場合、$${d\beta_1 / dt = 0}$$であることに注意して、

$${\displaystyle a = \frac{d\beta}{dt}\\\,\\\quad = \frac{1}{(1 + \beta_1\beta'_2)^2} \left\{ \frac{d\beta'_2}{dt}(1 + \beta_1\beta'_2)-(\beta_1+\beta'_2)\beta_1\frac{d\beta'_2}{dt} \right\} \\ \, \\ \quad =\frac{1-\beta_1^2}{(1 + \beta_1\beta'_2)^2}\frac{d\beta'_2}{dt}}$$　式4

ここで、

$${\displaystyle \frac{d\beta'_2}{dt} = \frac{d\beta'_2}{dt'} \frac{dt'}{dt}\\ \, \\ \quad \quad= a' \frac{\gamma_1 dt - \gamma_1 \beta_1 dx}{dt} \\ \, \\ \quad \quad = a' \gamma_1 \left(1-\beta_1 \frac{dx}{dt} \right) \\ \, \\ \quad \quad = a' \gamma_1 \left(1-\beta_1\frac{\beta_1 + \beta'_2}{1+\beta_1\beta'_2}\right) \\ \, \\ \quad \quad = a'\gamma_1 \frac{1-\beta_1^2}{1+\beta_1\beta'^2}}$$　式5

となるので（途中、式1の微分形と式3を使用）、これを式4に代入して、

$${\displaystyle a = a' \gamma_1 \frac{(1-\beta_1^2)^2}{(1+\beta_1\beta'_2)^3} \\ \, \\ \quad = a' \frac{(1-\beta_1^2)^{3/2}}{(1+\beta_1\beta'_2)^3}}$$　式6

が得られた（加速度の合成則と言うらしい）。

等加速度運動の静止系における軌跡

さて、次に上記のステップ(3)。式6を積分して、一様加速している観測者のS系のおける軌跡を求める。S'系に乗っている観測者は、加速はしているが、S'系における速度はゼロで、S'系に固定されている。従って、$${\beta'_2 = 0}$$, $${\beta = \beta_1}$$である。これらを式6に代入して、

$${\displaystyle a = \frac{d\beta}{dt} = a' (1-\beta^2)^{3/2}}$$

を得る。S'系における加速度は一定であるから、右辺の$${a'}$$は定数である。
この式は変数分離型であるので、簡単に積分できる。

$${\displaystyle \frac{d\beta}{(1-\beta^2)^{3/2}} = a'dt }$$

$${\displaystyle \int^\beta_0 \frac{d\beta}{(1-\beta^2)^{3/2}} = a' t }$$　式7

左辺は、$${\beta = \sin\phi}$$とおけば積分できる。
$${d\beta = \cos\phi d\phi = \sqrt{1-\beta^2}d\phi}$$
であるから、式7の左辺は、

$${\displaystyle \int^{\arcsin\beta}_0 \frac{d\phi}{1-\beta^2} = \int^{\arcsin\beta}_0 \frac{d\phi}{\cos^2\phi} \\\,\\ \quad = \tan(\arcsin\beta) \\\,\\\quad = \frac{\beta}{\sqrt{1-\beta^2}} }$$　式8

となる。$${\tan(\arcsin\beta)}$$に怯んではいけない。三角関数の意味を考えれば上式の通りになる。

式7, 8より、

$${\displaystyle \frac{\beta}{\sqrt{1-\beta^2}} = a' t }$$　式9

を得る。$${\beta}$$について解くと、

$${\displaystyle \beta = \frac{dx}{dt} = \frac{a't}{\sqrt{1 + a'^2 t^2}} }$$　式10

を得る。これは簡単に積分できて、

$${\displaystyle x = \sqrt{t^2 + \frac{1}{a'^2}} }$$　式11

が得られた。変形すると、

$${\displaystyle x^2 - t^2 = \frac{1}{a'^2}}$$　式12

となり、この軌跡は、時空図において下図のような双曲線となる。

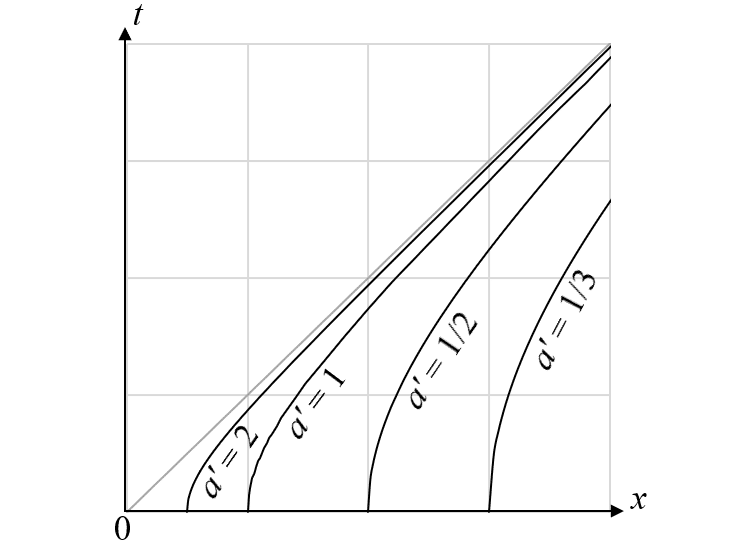
この図は、なかなか興味深い。S'系では一定加速度$${a'}$$で加速を続けていても、静止系Sから見るとその速度は無限に増大するわけではなく、光速のライン$${t = x}$$に漸近してしまう。$${a'}$$の値によって$${x}$$軸上の出発点（$${x = 1/a'}$$）と双曲線の曲がり具合が異なるが、漸近する直線は共通である（今の場合、上の積分の計算で、$${a'}$$の値に依らず漸近線が原点を通るように積分定数を選んでいる）。

座標変換式の導出

さて、等加速度運動の時空図における軌跡がわかったので、これにS'系の目盛りを振って、静止系Sと一様加速系S'の間の座標変換式を求めよう。

t’軸の目盛りを振る

$${t'}$$軸上の静止系における座標$${(t,x)}$$を、S'系の座標$${t'}$$ ($${x' = 0}$$) で表すことを考える。$${t'}$$は、一様加速系の原点に固定された観測者が見る時刻で、いわゆる固有時間である。これは、比較的容易に計算できる。

式1より、

$${\displaystyle dt' = \gamma dt - \gamma\beta dx}$$　式13
$${\displaystyle dx' = -\gamma\beta dt + \gamma dx}$$　式14

となる。$${t'}$$軸上では$${dx' = 0}$$であるので、式14より、$${\beta dt = dx}$$となる。これを式13に代入して、

$${\displaystyle dt' = \gamma (1-\beta^2)dt = \sqrt{1-\beta^2}dt}$$

これを積分すればよい。

$${\displaystyle t' = \int \sqrt{1-\beta^2}dt}$$

ここで、式11より、

$${\displaystyle \beta = \frac{dx}{dt} = \frac{t}{\sqrt{t^2+1/a'^2}}=\frac{t}{x}}$$　式15

が、$${t'}$$軸上の任意の点で成立するため、

$${\displaystyle t' = \int \sqrt{1-\left(\frac{t}{x}\right)^2}dt \\ \, \\ \quad = \int \frac{\sqrt{x^2-t^2}}{x}dt}$$

ここで、式11, 12を代入して、

$${\displaystyle t' = \int \frac{dt}{\sqrt{(a't)^2+1}} \\ \, \\ \quad = \frac{1}{a'}\log\left\{(a't)^2+\sqrt{(a't)^2+1}\right\}}$$　式16

となった（双曲線関数の有名な積分公式を使用）。$${t}$$について解いて、

$${\displaystyle t = \frac{1}{a'}\sinh a't'}$$　式17

を得る。さらに、これを式11に代入して、

$${\displaystyle x = \frac{1}{a'}\cosh a't'}$$　式18

を得る。式17, 18が、$${t'}$$軸上の座標の変換式である。

x'軸に目盛りを振る

導出に難渋したのが、$${x'}$$方向の目盛り付けである。$${t'}$$軸上の任意の点から$${x'}$$方向にある距離だけ動いたとき、その点のS系での座標$${(t, x)}$$は、$${t'}$$, $${x'}$$を用いてどのように書けるか？具体的な表式を求める前に、ちょっと物理的に考えてみる。

まず、$${x'}$$軸は時空図上でどのようになるべきか？$${t = t' = 0}$$のとき、$${x'}$$軸は当然ながら$${x}$$軸そのものである。S'系が加速して、その速度が$${\beta}$$になったときはどうなるか？まず、S'系にいる観測者は加速度運動をしているが、その加速度$${a'}$$は時間に依らず一定のため、S系から見た自分の速度がゼロだろうが、あるいは有限の値$${0 < \beta < 1}$$であろうが、自分が観測するS'系の世界はまったく変わらないはずである。なので、S'系の速度が$${\beta}$$であるとき、S系の観測者がそれを速度$${\beta}$$で追いかけて観測する場合、そのときの状況は、$${t = t' = 0}$$のときとまったく同じはずである。したがって、S'系の速度が$${\beta}$$のときの$${x'}$$軸は、$${x}$$軸を速度$${\beta}$$でローレンツ変換した直線

$${t  = \beta x}$$　式19

となる。時刻$${t'}$$が増大するにつれて、傾き$${\beta}$$も大きくなり、$${t = x}$$の漸近線に近づいていく。

さて、この直線上に何とかして目盛りを振りたい。そこで、$${x'}$$をゼロでない値に固定した状態で$${t'}$$を動かしたとき、その点の軌跡は時空図上でどのようになるか？を考える。$${t' = 0}$$の出発点は、$${x}$$座標は$${x = 1/a'}$$からずれた位置となる。このS系でみた$${x}$$座標を$${1/a'+\Delta x}$$としよう。今の段階では、まだ$${x}$$と$${x'}$$の関係が不明（それを求めようとしている）なので、S'系におけるこの点の座標$${x'}$$は不明である。この点は、出発後、任意の時刻で、S'系の原点に固定された観測者からは常に同じ距離だけ離れているように見えるわけだが、この点の軌跡はどうなるか？答えは、加速度$${(a'^{-1}+\Delta x)^{-1}}$$に対応する双曲線

$${\displaystyle x^2-t^2 = \left(\frac{1}{a'} + \Delta x\right)^2}$$　式20

すなわち、

$${\displaystyle x = \sqrt{t^2 + \left(\frac{1}{a'} + \Delta x\right)^2}}$$　式21

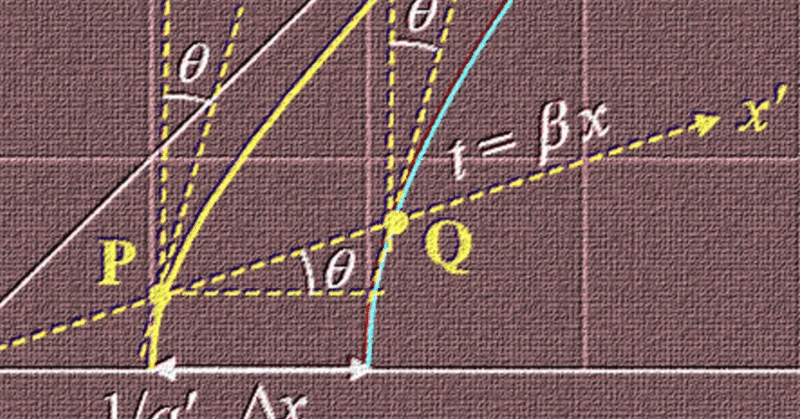
となる。理由は下図を眺めると分かる。図中で、$${\theta}$$はすべて$${\tan\theta= \beta}$$となる角度である。

上図で、赤線が、S'系においてつねに固定の座標（$${x'>0}$$）の点の軌跡である。なぜか？「赤線が、S'系においてつねに固定の座標（$${x'>0}$$）の点の軌跡である」ことの必要十分条件を考えると、

1) 上図のように、$${x'}$$軸である$${t = \beta x}$$の直線との交点をP, Qとした場合、いずれの点も、S系で観測する速度は$${\beta}$$に等しくなる

2) 2点P, Qはいずれも速度$${\beta}$$で動いているので、2点P, Qの$${x}$$座標の差分は、$${\gamma \Delta x}$$となる（ローレンツ収縮、図1参照）

の２つが成り立てばよい。(1)については、青線の$${t'}$$軸（式11）にしても、赤線（式21）にしても、$${dx/dt = t/x}$$が成り立つことから、すぐに分かる。(2)についても、任意の双曲線$${x^2-t^2 = C^2}$$と直線$${t = \beta x}$$の交点の$${x}$$座標が$${x = \gamma C}$$となることから、すぐに分かる。

以上の考察から、任意の$${x'}$$の場合の座標変換式は、$${t'}$$軸上の表式（式17, 18）を拡張して、

$${\displaystyle t = \frac{1}{a'} f(x') \sinh a't'}$$　式22

$${\displaystyle x = \frac{1}{a'} f(x') \cosh a't'}$$　式23

と書けるはずである。$${f(x')}$$は、$${x'}$$のみの関数で、上記$${\Delta x}$$に対応する部分である。

と、ここまで追い込んだのだが、、、$${f(x')}$$の関数形を求めるために、一体何を手掛かりにどう式を立てればよいのか、なかなか思いつかなかった。数日考えてようやく思い付いたのは、ローレンツ変換の$${t}$$軸と$${x}$$軸の対称性を使えばよい、というアイデアである。すなわち、ローレンツ変換では、$${t}$$軸と$${x}$$軸の単位ベクトルの長さが常に同じ（変換前後では長さは変わるが、同一座標系では$${|{\bold e}_t|=|{\bold e}_x|}$$）であるため、

$${\displaystyle \frac{dx}{dx'} = \frac{dt}{dt'}}$$　式24

が成り立つ。式22, 23に適用してみよう。

$${\displaystyle \frac{dt}{dt'} = f(x')\cosh a't'}$$　式25

$${\displaystyle \frac{dx}{dx'} = \frac{1}{a'}\dfrac{f(x')}{dx'}\cosh a't'}$$　式25

となり、式24より、

$${\displaystyle f(x')\cosh a't' = \frac{1}{a'}\dfrac{f(x')}{dx'}\cosh a't'}$$

となる。これが任意の$${t'}$$で成立するのだから、

$${\displaystyle f(x') = \frac{1}{a'}\frac{df(x')}{dx'}}$$

である。これは簡単に解けて、

$${\displaystyle f(x') = e^{a'x'}}$$

となった（$${f(x'=0)=1}$$と規格化）。従って、最終的なS系とS'系の座標変換式（リンドラー変換）

$${\displaystyle t = \frac{1}{a'} e^{a'x'} \sinh a't'}$$　式26

$${\displaystyle x = \frac{1}{a'} e^{a'x'} \cosh a't'}$$　式27

が得られた！　実にお疲れさまでした。。

おわりに

得られた式26, 27を改めて鑑賞すると、なかなか味わい深い。$${x'}$$は負の方向にいくらでも大きな値をとれるが、S系では、その座標は原点に収束してしまう。従って、S'系の原点に固定された観測者から見ると、$${x < 0}$$の世界はまったく見ることができない。言わば、$${x = 0}$$の点は、S'系の観測者にとっては、ブラックホールの事象地平線のように振舞うことになる。その他、このリンドラー座標系には、直観に反する不思議な性質がいろいろある。特に、一様加速する荷電粒子にこの座標系を適用して計算すると、電磁気学の基礎であるガウスの法則（閉曲面から出る正味の電場の積分値は、閉曲面内部の総電荷に等しいという基本則）が成立しなくなったり、電荷が加速度運動しているにもかかわらず、電磁波の放射が観測されなくなったり等、興味深い問題がある。これらについては、稿を改めて紹介する。