はじめに

　本稿でも、等加速度運動の相対論的な記述について紹介する。以下の記事の続きである。本稿の内容も、調べればどこかに解説されていることなので、自分のオリジナルな部分は特にない。表式を簡単にするため、前記事同様、以下で光速度$${c=1}$$とする単位系を使用する。

場所に寄らず一様な重力場があるとき、ニュートン力学によると、空中に放り投げた物体の軌道が2次曲線の放物線を描くことは、高校の物理で習う基本事項である。式で書くと、鉛直方向の速度と座標は、

$${\displaystyle v(t) = v_0 - gt}$$　式1

$${\displaystyle x(t) = x_0 - v_0t - \frac{1}{2}gt^2 }$$　式2

となる（鉛直上向きを$${+x}$$方向としている）。この表式では、時刻$${t}$$が大きくなると、速度$${v}$$もいくらでも大きくなってしまうが、相対論によれば、物体の速度は光速度を超えることはできないので、相対論的な放物線は、上式とは異なるものになるはずである。本稿では、一般相対論による放物線の導出を紹介する。

考える問題は、観測者が一様な重力場にいるときに、重力のみの影響を受ける物体の運動を求める、というものである。

一様な重力場は、静止系に対して一定の加速度で動く座標系とみなせるので、この問題を考えるには、相対論的な等加速度系を記述するリンドラー座標系を用いればよい。一般相対論によれば、重力のみ受ける物体の軌道はその座標系の測地線となるので、今の問題は、リンドラー座標系の測地線を求める問題に他ならない。なので、考える手順は、

1) リンドラー座標系の計量テンソルを求める
2) 接続係数を求める
3) 測地線方程式を立てる
4) それを解く

となる。意味が分かっていれば、機械的に計算するだけである。

計量テンソル・接続係数

静止系S$${(t, x)}$$と、等加速度系S'$${(t', x')}$$の変換式は以下となる（リンドラー変換）。

$${\displaystyle t = \frac{1}{g} e^{gx'} \sinh gt'}$$　式3

$${\displaystyle x = \frac{1}{g} e^{gx'} \cosh gt'}$$　式4

これらの式を微分すると、

$${\displaystyle dt = (e^{2gx'}\sinh gt')dx' + (e^{2gx'}\cosh gt')dt'}$$　式5

$${\displaystyle dx = (e^{2gx'}\cosh gt')dx' + (e^{2gx'}\sinh gt')dt'}$$　式6

となる。これらを用いて不変距離を計算すると、

$${\displaystyle (ds')^2 = -(dt)^2+(dx)^2 \\ \, \\ \quad = e^{2gx'}\{-(dt')^2+(dx')^2\} }$$　式7

となるので、計量テンソル$${g_{\mu\nu}}$$は、

$${\displaystyle g_{00} = -e^{2gx'}}$$
$${\displaystyle g_{11} = e^{2gx'}}$$　式8

となる（その他の成分はゼロ）。上付き添え字の方は、直ちに、

$${\displaystyle g^{00} = -e^{-2gx'}}$$
$${\displaystyle g^{11} = e^{-2gx'}}$$　式9

となる。次に、接続係数

$${\displaystyle \Gamma^\alpha_{\beta\gamma} := \frac{1}{2}g^{\alpha\mu}(g_{\mu\beta,\gamma} + g_{\mu\gamma,\beta} - g_{\beta\gamma,\mu})}$$　式10

を計算する。この定義式に従って式8, 9を用いて計算すると、

$${\displaystyle \Gamma^0_{10} = \Gamma^0_{01} = \Gamma^1_{00} = \Gamma^1_{11} = g}$$　式11

となる（それ以外の成分はゼロ）。

測地線方程式

以下で、表記を簡単にするため、等加速度系の座標に付けていたダッシュを外す。運動する物体の固有時を$${\tau}$$で表すと、一般相対論の測地線方程式は、

$${\displaystyle \frac{d^2x^\mu}{d\tau^2} + \Gamma^\mu_{\alpha\beta}\frac{dx^\alpha}{d\tau}\frac{dx^\beta}{d\tau} = 0}$$　式12

で与えられる。が、今求めたいのは、通常の座標時で表した物体の運動であるので、式12の固有時$${\tau}$$に関する微分を、座標時$${t}$$の微分に書き換えよう。物体が時空を動いていくとき、固有時$${\tau}$$と座標時$${t}$$は常に一対一の関係にあるので、微分の連鎖律

$${\displaystyle \frac{d}{d\tau} = \frac{dt}{d\tau}\frac{d}{dt}}$$

を適用することができる。これを用いると、

$${\displaystyle \frac{d^2x^\mu}{d\tau} = \frac{d}{d\tau}\left( \frac{dx^\mu}{dt} \frac{dt}{d\tau} \right) \\ \, \\ \quad = \left(\frac{d}{d\tau} \frac{dx^\mu}{dt}\right)\frac{dt}{d\tau}+\frac{dx^\mu}{dt}\frac{d^2t}{d\tau^2} \\ \, \\ \quad = \frac{d^2x^\mu}{dt^2}\left(\frac{dt}{d\tau} \right)^2 + \frac{dx^\mu}{dt} \frac{d^2t}{d\tau} }$$　式13

$${\displaystyle \frac{dx^\alpha}{d\tau} = \frac{dx^\alpha}{dt}\frac{dt}{d\tau}}$$　式14

となるので、これらを式12に代入すると、

$${\displaystyle \frac{d^2x^\mu}{dt^2}\left(\frac{dt}{d\tau} \right)^2 + \frac{dx^\mu}{dt} \frac{d^2t}{d\tau} + \Gamma^\mu_{\alpha\beta}\frac{dx^\alpha}{dt}\frac{dx^\beta}{dt}\left(\frac{dt}{d\tau} \right)^2 = 0}$$　式15

すなわち、

$${\displaystyle \frac{d^2x^\mu}{dt^2} + \frac{dx^\mu}{dt} \frac{d^2t}{d\tau}\left(\frac{d\tau}{dt} \right)^2 + \Gamma^\mu_{\alpha\beta}\frac{dx^\alpha}{dt}\frac{dx^\beta}{dt} = 0}$$　式16

が得られた。ここで第2項にある$${\tau}$$を消去したい。この式の$${\mu = 0}$$成分をとると（$${x^0 = t}$$であることに注意）、

$${\displaystyle \frac{d^2t}{d\tau^2}\left(\frac{d\tau}{dt} \right)^2+\Gamma^0_{\alpha\beta}\frac{dx^\alpha}{dt}\frac{dx^\beta}{dt} = 0}$$　式17

となるので、これを用いると、式16は、

$${\displaystyle \frac{d^2x^\mu}{dt^2} + \Gamma^\mu_{\alpha\beta}\frac{dx^\alpha}{dt}\frac{dx^\beta}{dt} - \frac{dx^\mu}{dt}\Gamma^0_{\alpha\beta}\frac{dx^\alpha}{dt}\frac{dx^\beta}{dt} = 0}$$　式18

となった。これが、座標時$${t}$$の微分で表した測地線方程式である。接続係数に式11を代入すると、

$${\displaystyle \frac{d^2x}{dt^2} -g \left(\frac{dx}{dt} \right)^2 + g = 0}$$　式19

が得られた。これが、一様重力場における放物線の運動方程式である。

方程式を解く

さて、解くべき方程式が得られたので、積分しよう。式19で$${v = dx/dt}$$と置くと、

$${\displaystyle \frac{dv}{dt} = -g(1-v^2)}$$　式20

となる。積分に入る前にこの式を観賞しよう。ニュートン力学の場合、これに相当する方程式は当然、

$${\displaystyle \frac{dv}{dt} = -g}$$　式21

となる。式20と見比べると、相対論的効果により$${gv^2}$$という項が付加されているわけである。式20を見ると、この項の効果はすぐに分かる。$${v}$$が光速よりも十分小さい（$${|v|\ll1}$$）場合、ニュートン力学の式21とほとんど変わらないが、速度が大きくなり光速度に近づくと（$${|v| \to 1}$$）、式20の右辺は実質ゼロになり、それ以上加速しなくなる。物体の速度が光速度を超えないという相対論的制約が、式20に組み込まれている。

さて、積分計算に入る。幸いにも式20は変数分離型で、

$${\displaystyle \frac{dv}{1-v^2} = -g dt}$$　式22

と変形できる。左辺を積分しよう。

$${\displaystyle \int \frac{dv}{1-v^2} = \frac{1}{2}\int\left( \frac{1}{1-v} + \frac{1}{1+v} \right)dv \\ \, \\ \quad = \frac{1}{2}\log\frac{1+v}{1-v} + C}$$　式23

となった（$${C}$$は積分定数）。式22より、

$${\displaystyle \frac{1}{2}\log\frac{1+v}{1-v} = -gt - C}$$

$${\displaystyle \therefore \frac{1+v}{1-v} = C'e^{-2gt}}$$　式25

となった（$${C'}$$は適当な定数）。ここで、$${t = 0}$$のときの$${v}$$初期値を$${v_0}$$とし、$${K_0 = (1+v_0)/(1-v_0)}$$と置くと、

$${\displaystyle v = 1 - \frac{2}{1+K_0e^{-2gt}}}$$　式26

となる。これが速度の時間変化を表す式である。この式からすぐに分かるように、
$${t \to -\infty}$$のとき、$${v\to+1}$$,
$${t \to +\infty}$$のとき、$${v\to-1}$$
となる。物体は、光速に近い速度で上昇してきて減速して反転し、下向きに加速して光速に近づいていくわけである。

次に、式26を積分して、位置$${x}$$を時刻$${t}$$で表そう。

$${\displaystyle x = \int vdt \\ \, \\ \quad = t - \int\frac{2e^{2gt}}{e^{2gt}+K_0}dt \\ \, \\ \quad = t - \frac{1}{g}\log(e^{2gt}+K_0)+C \\ \, \\ \quad = t - \frac{1}{g}\log\left(e^{2gt}+\frac{1+v_0}{1-v_0}\right)+C}$$　式27

となった（$${C}$$は積分定数）。これが、一様重力場における相対論的な放物線の表式である。

ニュートン力学との比較

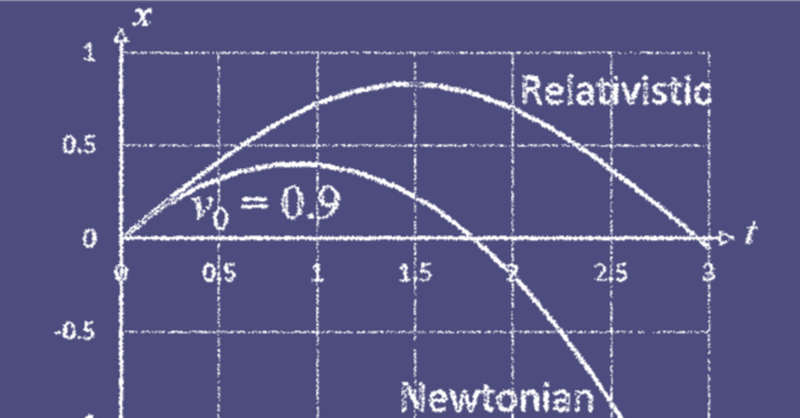
放物線の式が導出できたので、初速度$${v_0}$$が同じ場合で、ニュートン力学と一般相対論で放物線の形状がどう異なるか、図示してみよう。以下に、$${v_0 = 0,\,0.5,\,0.9}$$の3つの場合を順に示した。赤線がニュートン力学、青線が一般相対論の場合である。いずれも、$${t = 0}$$付近では一致しているが、$${t}$$が大きくなるにつれてズレが大きくなり、相対論の方では、光速（傾きが-1）に漸近するのが分かるだろう。

ここでおもしろいのは、3番目の$${v_0 = 0.9}$$の場合である。ニュートンでも相対論でも、上に放り投げた物体は反転して落ちてくるわけだが、最高点の高さが異なるのだ。ニュートン力学の場合、運動方程式は、

$${\displaystyle \frac{dv}{dt}+g=0}$$　式28

であり、$${v = dx/dt}$$を掛けると、

$${\displaystyle v\frac{dv}{dt} + g\frac{dx}{dt} = 0 \\ \, \\ \therefore \frac{d}{dt}\left( \frac{v^2}{2}+gx\right) = 0}$$　式29

となる。これはよく知られた力学的エネルギー保存則である。ニュートン力学では、上に放り投げた物体の最高点の高さは、この保存則を利用して容易に求めることができるが、一般相対論この法則が成立しないのだ。相対論的な運動方程式は、式20である。これを同様に計算すると、

$${\displaystyle \frac{d}{dt}\left( \frac{v^2}{2}+gx\right)=v^3}$$　式30

となり、ニュートン的力学的エネルギーが保存量にならないのである。この辺は注意が必要だろう。

おわりに

以上、相対論的な放物線でした。前記事の双子のパラドックスの解法でもそうだが、リンドラ―座標の場合、積分が初等的に計算可能であるが本当にありがたいのである。次は、リンドラ―座標系の事象地平面や、電磁気学のガウスの法則の破綻について紹介する。リンドラーネタは続く。