一様加速する電荷は電磁波を放射するか?―電磁気学の奥深すぎるパラドックス―
はじめに
等加速度運動を相対論的に記述するリンドラー座標について、これまでに以下の5本の記事を書いた。
①リンドラー座標を自力で導出してみた―等加速度運動の相対論的記述―
②リンドラー座標つれづれ(1)―双子のパラドックス―
③一般相対論的放物線―リンドラー座標つれづれ(2)―
④事象の地平面、ガウスの法則の破綻?—リンドラー座標つれづれ(3)―
⑤無限遠にある電荷がガウスの法則を取り戻す―リンドラー座標つれづれ(4)—
これで、ようやく本丸の問題に取り掛かる準備が整った。それは、
等加速度運動をする電荷は、電磁波を放射するか?
という問題である。2022年の夏のある日、車を運転中渋滞にはまったので、頭の中で物理の問題を考えて時間を潰していたのだが、ふと、以下のような疑問が浮かんだ。
同じ質量の物体A, Bがあり、物体Aは帯電せず、物体Bは帯電している。これら2つの物体を一様重力下で自由落下させた場合、どちらが速く落ちるか?
高校レベルの物理の知識だったら、電荷のありなしに関わらず同じ速さで落ちるのでは?と答えるだろう。ところが、大学学部レベルの電磁気学の知識があると、回答は変わる。一般に、電荷が加速度運動すると、電磁波を放射する。これは、電荷から見ると、真空中の電磁場から抵抗を受けて、電磁場を引きずりながら進むようなもので、その結果として、周囲の電磁場が揺り動かされ、そのさざ波が遠方に伝播して行く。これが起きるのはあくまで加速度運動をしている場合であって、等速直線運動をするときには、これはまったく起きない。というわけで、帯電している物体Bの方が、落ちるのは遅くなりそうである。
ところがこの問題、その後調べてみると、ものすごく奥が深い問題であることを知る。上記の問題は、さらに考察を進めると、何と一周回って、物体AもBも同じ加速度で落ちる、が正解となるようである。一様加速運動の場合、帯電した物体は、電磁波は放射するが、電磁場からの抵抗(いわゆる放射の反作用)は受けない、という奇妙な振る舞いをするらしい。
この一様加速する電荷の奇妙な振る舞いは、何と、パウリ、ボルン、ゾンマーフェルト、ファインマン等の著名な物理学者も論争に加わったほどの問題だったようだが、現在では、少なくとも放射するか否かについては、解決を見ているようである(放射の反作用については議論があるようだが)。今世紀に入ってから、この問題について再考する論文がいくつか出ており、問題が整理されて、単純明解な解法を示した論文も出てきた。しかも、この問題の本質的な部分は、電磁気学と一般相対論の基礎知識があれば、十分理解できるものである。本稿では、私の理解に基づいて、この問題を解説する。
論点を整理
ややこしい問題なので、論点を整理しよう。論点は、大きく分けて、以下の2つである。
①等加速度運動をする電荷は、電磁波を放射するか?
②電磁波を放射する場合、エネルギーの保存はどうなっているのか?
論点①は、上述の私の疑問そのもので、一般相対論も絡む問題である。慣性系に観測者が静止していて、慣性系においてる電荷が一様加速運動をする状況を考える。通常の電磁気学では、一様加速する電荷は電磁波を放射することになる。一方、観測者が電荷と一緒に動く座標系に固定されたらどうなるか?その座標系では、観測者から見ると電荷は静止しているので、電磁波の放射は観測されないはず。観測者の運動状態によって、電荷からの放射が観測されたり、されなかったりするのは矛盾ではないか?
先に答えを言ってしまうと、放射の観測の可否が観測者の運動状態に依存するのは、正しい、ようである。直観的には理解しがたい話だが、非常に巧妙な仕組みで成立するのだ。私の元々の関心はこの問題だったので、本稿で詳しく解説する。
論点②の方は、問題自体が少々複雑である。古典電磁気学を用いて一様加速する電荷が受ける放射の反作用を計算すると、どうしてもゼロになってしまう。反作用を受けているはずなのに、それが何かで相殺されているとしたら、その力は一体どこから来るのか?という問題である。この論点は、深く入り込むと、放射の反作用そのものの妥当性の議論になるので、本稿では割愛する。
以下、下記の論文を参照して解説する。
論文1: C. de Almeida & A. Saa, 2005. The radiation of a uniformly accelerated charge is beyond the horizon: a simple derivation. arXiv:physics/0506049v5.
論文2: J. Franklin & D. J. Griffiths, 2014. The fields of a charged particle in hyperbolic motion. American Journal of Physics, 82(8): 755-763.
論文3: T. Fulton & F. Rohrlich, 1960. Classical Radiation from a Uniformly Accelerated Charge. Annals of Physics, 9: 499-517.
論文4: D. Boulware, 1980. Radiation from a Uniformly Accelerated Charge. Annals of Physics, 124: 169-188.
論文5: T. Hirayama, 2001. Bound and Radiation Fields in the Rindler Frame. Progress of Theoretical Physics, 106(1): 71-97.
観測者が慣性系に静止している場合
ここからしばらく論文1に沿って解説する。まず、通常の電磁気学の前提通り、慣性系に観測者が静止していて、電荷$${q}$$が慣性系において一様加速度運動をする場合を考えよう。この場合、電荷が電磁波を確かに放射することを示す。以下で、光速度を$${c = 1}$$とし、CGS単位系で表記する。また、時空の計量テンソルの符号は$${(+, -, -, -)}$$とする。
電磁場の導出
電荷は$${z}$$軸に沿って、相対論的な等加速度運動をすると想定する。電荷は、$${t = -\infty}$$, $${z = +\infty}$$から原点に向かって移動してきて、$${t = 0}$$に$${z = b > 0}$$で折り返し、$${t = +\infty}$$に$${z = +\infty}$$へ飛び去って行く。電荷の固有加速度を$${g}$$、電荷の固有時を$${\tau}$$とすると、電荷の4元座標は、以下のような双曲線で表される。
$${\displaystyle t \equiv r^0(\tau) = \frac{1}{g}\sinh g\tau \\ x\equiv r^1(\tau) = 0 \\ y\equiv r^2(\tau) = 0 \\ z\equiv r^3(\tau) = \frac{1}{g}\cosh g\tau}$$ 式1
時空図における電荷の軌道を図示すると、下図の赤線のようになる。
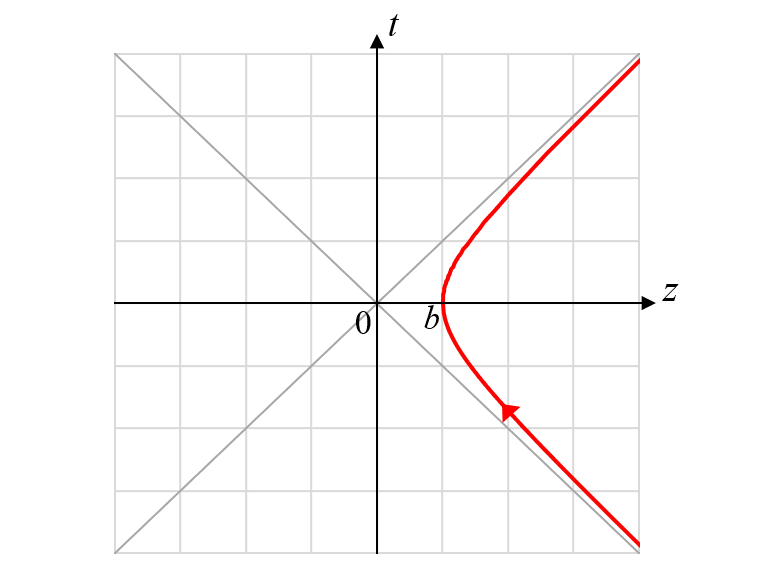
折り返し地点の座標は、$${b = 1/g}$$である。軌道は$${t \to \pm\infty}$$で直線$${t \mp z = 0}$$に漸近する。
この電荷が形成する電磁場を求めよう。電磁場テンソル
$${F^{\mu\nu} = \begin{bmatrix}0 & -E_x & -E_y & -E_z \\ E_x & 0 & -B_z & B_y \\ E_y & B_z & 0 &-B_x \\ E_z & -B_y & B_x & 0\end{bmatrix}}$$ 式2
の各成分を求めたい。ここで、運動する点電荷が形成する電磁場について、以下のような便利な公式がある(ジャクソン電磁気学に載っているもので、論文1を読んで初めて知った)。
$${\displaystyle F^{\mu\nu}(x) = \left[\frac{q}{V^\lambda(x_\lambda-r_\lambda)}\frac{d}{d\tau}\frac{(x^\mu-r^\mu)V^\nu-(x^\nu-r^\nu)V^\mu}{V^\lambda(x_\lambda-r_\lambda)} \right]_\text{ret}}$$ 式3
ここで、$${x^\mu}$$と$${r^\mu}$$はそれぞれ観測点と電荷の4元座標であり、$${V^\mu = d r^\mu/d\tau}$$は電荷の固有速度である。右辺はすべて電荷の遅延時刻において求める。$${V^\mu}$$のゼロでない成分は、式1より、
$${\displaystyle V^0 = \frac{dr^0}{d\tau} = \cosh g\tau\\ \, \\ \displaystyle V^3 = \frac{dr^3}{d\tau} = \sinh g\tau}$$ 式4
の2つである。観測点と電荷の遅延時刻における位置は、同一の光円錐上に乗らないといけない。そのための条件は、2点間の不変距離がゼロ
$${\displaystyle \left\{ x^\mu - r^\mu(\tau_\text{ret})\right\}\left\{ x_\mu - r_\mu(\tau_\text{ret})\right\} = 0}$$ 式5
である。これに式1を代入して計算すると、$${\rho = \sqrt{x^2 + y^2}}$$として、
$${K(\tau_\text{ret})\equiv \displaystyle z \cosh g\tau_\text{ret} - t \sinh g\tau_\text{ret} \\ \, \\ \quad = \frac{g}{2}\left(\rho^2 + z^2 - t^2 + \frac{1}{g^2} \right)}$$ 式6
を得る。また、$${W \equiv V^\lambda(x_\lambda-r_\lambda)}$$に式1, 2を代入すると、
$${\displaystyle W = t \cosh g\tau - z\sinh g\tau}$$ 式7
$${\displaystyle \frac{dW}{d\tau} = -gK}$$ 式8
を得る。計算すると分かるが、$${W}$$と$${K}$$は、任意の$${\tau}$$で、
$${\displaystyle W^2 - K^2 = z^2 - t^2}$$ 式9
の関係が成り立つ。これより、$${\tau = \tau_\text{ret}}$$のとき、
$${\displaystyle W(\tau_\text{ret})^2 = K(\tau_\text{ret})^2 + z^2 - t^2 \\ \, \\ \quad = \frac{1}{4b^2}\left\{ \left(\rho^2+z^2-t^2+b^2 \right)^2 - 4b^2\left(z^2-t^2\right)\right\} \\ \, \\ \quad = \frac{1}{4b^2}\left\{\left(\rho^2+z^2-t^2-b^2 \right)^2 +4b^2\rho^2\right\}}$$ 式10
を得る。
以上で道具立てが揃った。式3を用いて電磁場の具体的な表式を求めよう。
$${\displaystyle E_x = F^{10} \\ \, \\ \quad = q\left[\frac{1}{W} \frac{d}{d\tau}\frac{\left(x^1-r^1\right)V^0}{W} \right]_\text{ret} \\ \, \\ \quad = qx\left[ \frac{1}{W}\frac{d}{d\tau}\frac{V^0}{W}\right]_\text{ret} \\ \, \\ \quad = \frac{q}{b}\frac{xz}{W^3}}$$ 式11
省略したが、計算するとこうなる。同様に、
$${\displaystyle E_y = F^{20} = \frac{q}{b}\frac{yz}{W^3}}$$ 式12
となる。$${E_z}$$は、少々計算して、
$${\displaystyle E_z = F^{30} \\ \, \\ \quad = q\left[\frac{1}{W} \frac{d}{d\tau}\frac{\left(x^3-r^3\right)V^0-\left(x^0-r^0\right)V^3}{W}\right]_\text{ret} \\ \, \\ \quad = q\left[ \frac{1}{W}\frac{d}{d\tau}\frac{-g^2+K}{W} \right]_\text{ret} \\ \, \\ \quad = \frac{q}{2b}\frac{z^2-\rho^2-t^2-b^2}{W^3}}$$ 式13
となる。
※ここで、計算途中、$${K}$$も$${\tau}$$に依存することに注意。参照した論文1では、何とこの時間依存性を見落としており、$${E_z}$$の表式が間違っている。
同様に磁場も計算すると、
$${\displaystyle B_x = F^{32} = -\frac{q}{b}\frac{yt}{W^3}}$$ 式14
$${\displaystyle B_y = -F^{31} = \frac{q}{b}\frac{xt}{W^3}}$$ 式15
$${\displaystyle B_z = F^{21} =0}$$ 式16
を得る。これで電磁場の成分をすべて観測点の座標で表すことができた。改めて書き直すと、電場と磁場は、$${z}$$軸の周りの円柱座標$${(\rho,\phi,z,t)}$$を用いて、それぞれ以下のようになる(ハットが付いているのは単位ベクトル)。
$${\displaystyle \bold E = 4qb^2\frac{\left(z^2-\rho^2-t^2-b^2 \right)\hat{ \bold z} + 2z\rho\hat\rho}{\left\{ \left(\rho^2+z^2-t^2-b^2 \right)^2+4b^2\rho^2 \right\}^{3/2}}\theta(z+t)+2q\frac{\rho\hat\rho}{\rho^2+b^2}\delta(z+t) }$$ 式17
$${\displaystyle \bold B = 4qb^2\frac{ 2\rho t \hat\phi}{\left\{ \left(\rho^2+z^2-t^2-b^2 \right)^2+4b^2\rho^2 \right\}^{3/2}}\theta(z+t)-2q\frac{\rho\hat\phi}{\rho^2+b^2}\delta(z+t) }$$ 式18
ここで、第1項に掛かる階段関数$${\theta(z+t)}$$は、電荷が形成する場を、電荷の遅延時刻における位置を頂点とする光円錐の内側に限定するためにある。デルタ関数$${\delta(z+t)}$$が掛かる第2項は、式3からは直接導出できず、後付けに付加したもので、その光円錐の境界でガウスの法則を成立させる役割をする(その深淵なる意味については前の記事を参照)。
電磁波の放射
電磁場が求められたので、この電荷が確かに電磁波を放射していることを確かめよう。そのためには、電荷の任意の位置$${(0, 0, r^1(\tau_\text{ret}))}$$を中心として半径$${R}$$の球面を設定し、球面を外向きに出るポインティングベクトル$${\bold S = \bold E\times\bold B}$$の面積分を求め、$${R\to\infty}$$の極限をとったときに有限の量が残ることを示せばよい。式17, 18を用いて計算すればよいのだが(デルタ関数の項は放射に寄与しないので無視可)、なかなか大変なので、結果だけを示す(計算法は論文2, 3を参照)。放射のパワー(単位時間当たりに放射するエネルギー)は、
$${\displaystyle P = \frac{2q^2}{3b^2}=\frac{2}{3}q^2g^2}$$ 式19
となる。電荷の固有加速度の2乗に比例するという結果だが、意外な結果である。慣性系に静止した観測者から見ると、電荷の見かけの加速度$${a}$$は、電荷の速度が速くなるほど小さくなる($${a = g/\gamma^3}$$)が、放射のパワーは、見かけの加速度ではなく、固有加速度$${g}$$で決まるのだ。なので、電荷は時間に依らず一定のパワーで電磁波を放射することになる。
観測者が電荷と一緒に動く場合
次に、観測者が電荷と一緒に動く座標系に固定されている場合には、上記の電磁場が静的な電場に見えることを示す。この場合、観測者が乗る座標系(リンドラー座標系)は慣性系ではないので、一般相対論を用いて議論する必要がある。
電磁場の導出
観測点のリンドラー座標を$${x'^\mu(x) = (\tau(t,z),x,y,\xi(t,z))}$$とする。慣性系座標との変換式を、論文1に倣って、
$${\displaystyle t= \sqrt{\frac{2\xi}{g}}\sinh g\tau}$$ 式20
$${\displaystyle z= \sqrt{\frac{2\xi}{g}}\cosh g\tau}$$ 式21
とする($${\xi > 0}$$)。これまでの記事で用いていた変換式と空間座標部分が異なるが、そこは本質ではなく、上式のように$${\sinh g\tau}$$, $${\cosh g\tau}$$に共通の因子として掛かればよい。この座標系では、電荷の位置の$${\xi}$$座標は$${\xi=1/2g}$$となる。この座標系での微小不変距離は、
$${\displaystyle ds^2 = g_{\mu\nu}dx'^\mu dx'^{\nu}\\ \, \\ \quad = 2g\xi d\tau^2 - dx^2 - dy^2 - \frac{d\xi^2}{2g\xi}}$$
となる。$${G \equiv |\det(g_{\mu\nu})| = 1}$$である。式20, 21で導入した座標$${(\tau, x, y, \xi)}$$表せるのは、時空図の領域Iのみである(下図)。(この辺の事象の地平面については、以前の記事を参照。)
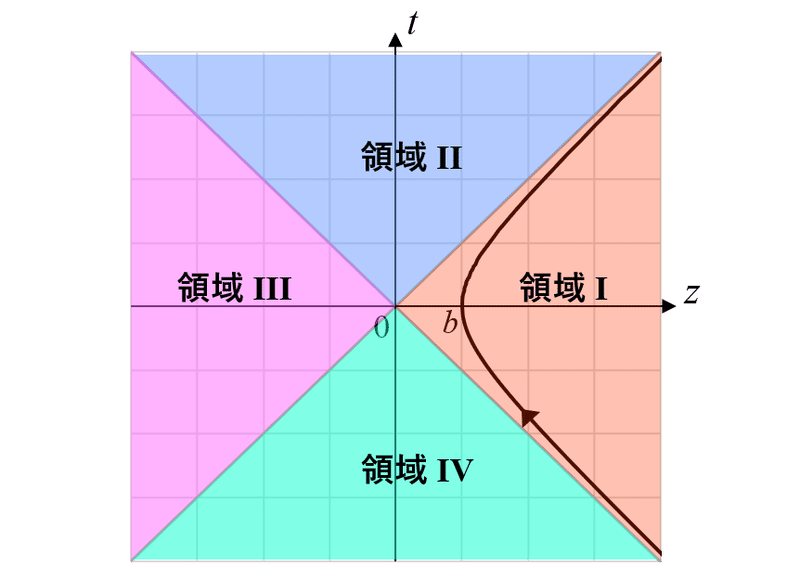
電荷と一緒に動く座標系に乗ると、観測者が存在可能な範囲は領域Iに限られる。慣性系に固定された観測者から見て、電荷の形成する電磁場が存在しうるのは領域IおよびⅡである。
式20, 21において、空間座標$${\xi}$$を固定して、時刻$${\tau}$$を電荷の固有時刻と同じにすれば、この座標系に乗った観測者は、電荷と空間的に距離を保ったまま、$${\xi=1/2g}$$に静止している電荷を観測することになる。
さて、この座標系に固定された観測者は、電荷が形成する電磁場がどのように見えるだろうか?それを考察するには一般相対論が必要となる。電磁気学を一般相対論的に書き換えると、マクスウェル方程式は、以下のようなテンソル形式で表現できる。
$${\displaystyle \partial_\lambda F_{\mu\nu} + \partial_\mu F_{\nu\lambda} + \partial_\nu F_{\lambda\mu} = 0}$$ 式22
$${\displaystyle \partial_\lambda (\sqrt{G}F^{\lambda\mu})= 4\pi\sqrt{G}J^\mu}$$ 式23
ここで、$${G = |\det g_{\mu\nu}|}$$、$${J^\mu}$$は4元電流である。一般に、曲がった時空でこの方程式を直接解いて電磁場テンソル$${F^{\mu\nu}}$$を求めるのは大変そうであるが、今の場合、慣性系における$${F^{\mu\nu}}$$は上述の通り既に得られているので、リンドラー座標系における電磁場を求めるには、慣性系における$${F^{\mu\nu}}$$に対して、以下のような座標変換
$${\displaystyle F'^{\mu\nu} = \frac{\partial x'^\mu}{\partial x^\alpha} \frac{\partial x'^\nu}{\partial x^\beta}F^{\alpha\beta}}$$ 式24
を施せばよい。一般相対性原理の凄みというか、ありがたみを実感するところである。
式24を用いて、まず磁場成分を計算してみよう。まず、
$${\displaystyle F'^{12} = \frac{\partial x'^1}{\partial x^\alpha} \frac{\partial x'^2}{\partial x^\beta}F^{\alpha\beta} = \frac{\partial x'^1}{\partial x^1} \frac{\partial x'^2}{\partial x^2}F^{12}\\ \, \\ \quad = F^{12} = -B_z = 0}$$ 式25
となる(式18より慣性系では$${B_z = 0}$$)。同様に、$${F'^{13}}$$, $${F'^{23}}$$も計算すると、
$${\displaystyle F'^{13} = \frac{\partial x'^1}{\partial x^1}\left(\frac{\partial x'^3}{\partial x^0}F^{10}+\frac{\partial x'^3}{\partial x^3}F^{13} \right) \\ \, \\ \quad = \frac{\partial \xi}{\partial t}E_x + \frac{\partial \xi}{\partial z}B_y}$$ 式26
$${\displaystyle F'^{23} = \frac{\partial x'^2}{\partial x^2}\left(\frac{\partial x'^3}{\partial x^0}F^{20}+\frac{\partial x'^3}{\partial x^3}F^{23} \right) \\ \, \\ \quad = \frac{\partial \xi}{\partial t}E_y - \frac{\partial \xi}{\partial z}B_x}$$ 式27
となる。式11-16を代入すると、
$${\displaystyle \frac{F^{13}}{x}=\frac{F^{23}}{y} = \frac{qg}{W^3}\left( \frac{\partial\xi}{\partial t}z+\frac{\partial\xi}{\partial z}t \right) }$$ 式28
を得る。ここで、式20, 21より、
$${\displaystyle \frac{\partial \tau}{\partial t} = \frac{z}{2\xi},\,\,\frac{\partial \tau}{\partial z} = -\frac{t}{2\xi},}$$ 式29
$${\displaystyle \frac{\partial \xi}{\partial t} = -gt,\,\,\frac{\partial \xi}{\partial z} = gz}$$ 式30
となるので、これらを式28に代入すると、
$${F'^{13} = F'^{23} = 0}$$ 式31
となる。式25, 31より、リンドラー座標系に固定した観測者から見ると磁場はゼロである。
次に電場成分を計算しよう。磁場成分とまったく同様に計算すると、
$${\displaystyle F'^{10} = \frac{1}{2\xi}\left(z E_x - tB_y\right) = \frac{qx}{W^3}}$$ 式32
$${\displaystyle F'^{20} = \frac{1}{2\xi}\left(z E_y + tB_x\right) = \frac{qy}{W^3}}$$ 式33
$${\displaystyle F'^{30} = \frac{g}{2\xi}E_z\left(z^2 -t^2\right) \\ \, \\ \quad = \frac{g}{2\xi}\frac{qg}{2W^3}(z^2-t^2-\rho^2-b^2)(z^2-t^2) \\ \, \\ \,\quad = \frac{qg}{2W^3}\left(\frac{2\xi}{g}-\rho^2-b^2\right)}$$ 式34
のようになった。
電場は静的
これで、リンドラー観測者からは電場のみ観測されることが分かったが、さて、これらは静的な場だろうか?それを確認するには、上記を$${x'^0 = \tau}$$で微分してみればよい。式32-34で$${W}$$が$${\tau}$$に非依存ならば、電場も$${\tau}$$に非依存となるのはすぐに分かる。そのために、電荷の遅延時刻における位置$${(g^{-1}\sinh g\tau_\text{ret},0,0,g^{-1}\cosh g\tau_\text{ret})}$$と、観測点の位置$${(\sqrt{2\xi/g}\sinh g\tau, 0, 0, \sqrt{2\xi/g}\cosh g\tau)}$$の関係を改めて確認する。これら2点の座標は、光円錐条件(式9)より、
$${\displaystyle K= \sqrt{\frac{2\xi}{g}}\cosh\left\{g(\tau - \tau_\text{ret}) \right\} = \frac{g}{2}\left( \frac{2\xi}{g} + \frac{1}{g^2} \right) }$$ 式35
が成り立つ。これより、観測点に対応する遅延時刻は、
$${\displaystyle \tau_\text{ret} = \tau - \frac{1}{g}\cosh^{-1}\left\{\sqrt{\frac{g}{2\xi}}\left(\xi+\frac{1}{2g} \right) \right\}}$$ 式36
となる。これより、
$${\displaystyle \frac{\partial \tau_\text{ret}}{\partial \tau} = 1}$$ 式37
が成り立つ。これを用いると、
$${\displaystyle W \equiv t\cosh g\tau_\text{ret} - z \sinh g\tau_\text{ret} = \sqrt{\frac{2\xi}{g}}\sinh\left\{g(\tau-\tau_\text{ret}) \right\}}$$ 式39
の$${\tau}$$による微分は、
$${\displaystyle \frac{\partial W}{\partial \tau} =\sqrt{2\xi g} \cosh \left\{ g(\tau-\tau_\text{ret})\right \} \frac{\partial}{\partial\tau}(\tau-\tau_\text{ret}) = 0}$$ 式40
とゼロになることが確認できた。したがって、リンドラー観測者が観測する電場は静的
$${\displaystyle \frac{\partial F'^{10}}{\partial \tau} = \frac{\partial F'^{20}}{\partial \tau} = \frac{\partial F'^{30}}{\partial \tau} = 0}$$ 式41
である!
矛盾はないのか?
以上長々と計算してきたが、よくよく考えてみると、マクスウェル方程式の1つの
$${\displaystyle \partial_\lambda (\sqrt{G}F^{\lambda\mu})= 4\pi\sqrt{G}J^\mu}$$ 式23再掲
において、観測者が電荷と一緒に動く座標系では、電荷は静止しているのだから、右辺の4元電流のうち、電流成分はすべてゼロ$${J^i= 0}$$ $${(i = 1, 2, 3)}$$である。電流が存在しないのだから、磁場も当然ゼロであり、電磁場が静的な電場のみになるのは、計算するまでもなく自明だったと言える。とにかく、慣性系で電磁波を放射する電磁場は、電荷と一緒に動く座標系に一般相対論的に変換すると、静的な電場になるのだ。
これで、
観測者が慣性系に静止している場合、電荷は電磁波を放射する
観測者が電荷と一緒に動く場合、電磁波は放射しない(静電場のみ観測される)
となることが確認できた。電磁波の観測の可否が、観測者の運動状態に確かに依存するわけだが、これで納得できただろうか?いや、そう単純には行かないでしょう。すぐに思いつく疑問は、以下のようなものである。
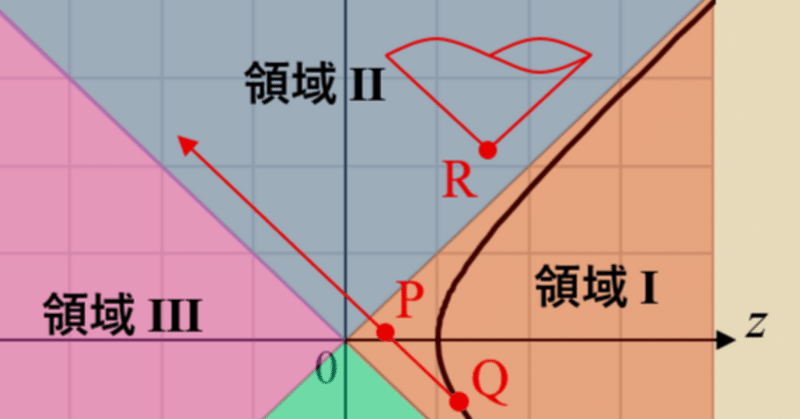
例えば、下図で、電荷が点Qで電磁波を放射した場合、放射は領域Iを通って領域Ⅱに入るわけだが、慣性系に固定された観測者は、領域Iにある通過点Pにおいても、放射された電磁波を観測できるのではないか?その場合、電荷と一緒に動く観測者が静的な場しか観測できないのは変ではないか?
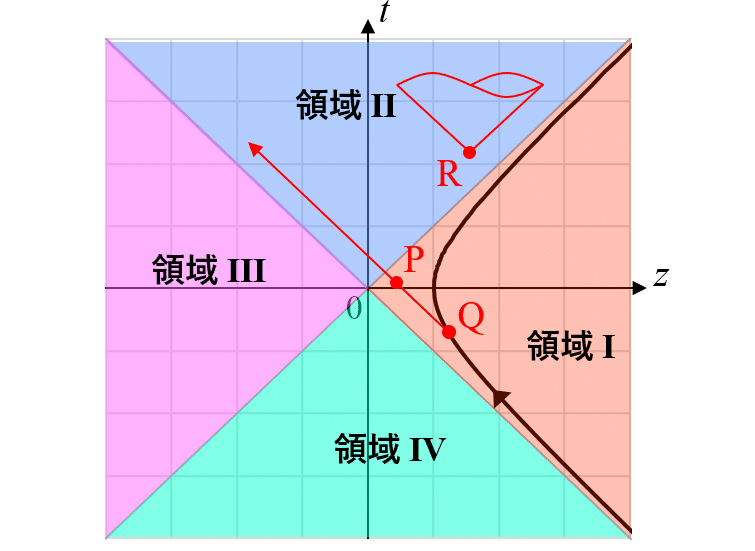
Qからの放射がPを通過するなら、Pで放射を観測できるのでは??
時空のある点で放射が通過するのを観測できる場合、運動状態が異なるだけの観測者にとって、同じ点にいるのに放射が見えなくなるのは変では?という疑問である。実は、ここがこの問題の奥深い点の1つで、何と、領域I内では、慣性系に固定した観測者でも、放射は観測できない、というのが答えのようである。
そもそも、電荷が電磁波を放射しているか否かを判定するには、上述したように、遅延時刻における電荷の位置を中心として、無限に大きい半径の球面を外向きに出るポインティングベクトルの面積分が正の値になるか否かを調べる必要がある。すなわち、遅延位置から観測点までの距離を$${R}$$として、$${R}$$が十分大きいときに、ポインティングベクトルに$${R^{-2}}$$に比例する成分があれば、無限遠方までエネルギーを運ぶことができるので、放射があると判定される。図3の点Pのような中途半端な距離にある観測点においては、$${R^{-2}}$$に比例する放射場の他、$${R^{-4}}$$に比例する束縛場(電荷に付随して一緒に動くだけの電磁場)の両方が寄与し、それらを区別することができない。このような意味で、電荷からの放射を観測できるのは、放射が伝播した先である領域Ⅱに限られる、らしい(論文3)。うーむ、、、釈然としないが、まあ、論理的にはそうなりそうである。
上記を認めれば、領域Iでは、慣性系に静止した観測者も、電荷と一緒に動く観測者も、放射を観測できない。一方、慣性系に静止した観測者は、領域Ⅱにおいて放射を観測することができる。
では、電荷と一緒に動く観測者から領域Ⅱを見るとどうなるか?というと、そもそも見ることができないのである。図3に示したように、領域Ⅱにある点Rを起点とする光円錐は、領域Iには届かないので、電荷と一緒に動く観測者にとっては、知りようがない。
整理すると、
領域Iでは、慣性系に静止した観測者も、電荷と一緒に動く観測者も、放射は観測できないので、矛盾なし
領域Ⅱでは、慣性系に静止した観測者は放射を観測できるが、電荷と一緒に動く観測者にとっては、事象の地平面の向こう側の話なので知ったことではなく、矛盾なし
ということである。実に、想像の斜め上を行く整合のとられ方ではないだろうか。
では、問題の設定を変えてみよう。今考えている問題で観測者と電荷を入れ替えて、慣性系に固定された電荷を、一様加速する観測者が観測したらどうなるか?論文1の最後の方にちらっと書いてあるが、何と、この場合、観測者は放射を観測できるようである。
ということは要するに、観測者と電荷のどちらが静止しているかは問題ではなく、それらの相対加速度によって、放射の観測の可否が決まると言えるだろうか?答えはYESのようである。日本人の平山亨さんという方が、この一般化した問題について論文5で明解な回答を示している。この論文を眺めると数式だらけで、式を追うのに半年くらいかかりそうな内容だが、ネットで検索すると、京都産業大学における平山さんの同内容の博士論文の要旨を日本語で読むことができる。それによると、この論文では、観測者が加速系にいる場合に、荷電粒子からの電磁波とは何かを数学的に明確にすることが目的とのことで、なかなか迫力ありそうな内容である。同論文では、荷電粒子と観測者の相対的な加速系に関する、以下の4つの場合
A. 荷電粒子、観測者ともに慣性系
B. 荷電粒子は一様加速、観測者は慣性系
C. 荷電粒子は慣性系、観測者は一様加速
D. 荷電粒子、観測者ともに一様加速系
について議論しており、B, Cの場合に荷電粒子からの電磁波を観測できる、らしい。やはり。
おわりに
以上で、元々自分の関心事であった、一様加速する電荷は電磁波を放射するか?の疑問については概ね納得に至った。冒頭で述べた、帯電した物体も帯電してない物体も同じ加速度で自由落下するというのは、以下のようなカラクリである。加速度運動する電荷の運動方程式として、Abraham-Lorentz-Dirac方程式というのが知られている:
$${\displaystyle m\frac{dv^\mu}{d\tau} = F^\mu_\text{ext}+\Gamma^\mu\,; \\ \, \\ \Gamma^\mu \equiv \frac{2e^2}{3}\left(\frac{d^2v^\mu}{d\tau^2}-v^\mu\frac{dv_\lambda}{d\tau}\frac{dv^\lambda}{d\tau} \right)}$$ 式42
$${F^\mu_\text{ext}}$$が外力で、$${\Gamma^\mu}$$が放射の反作用である。ここで、一様加速の場合、簡単な計算で$${\Gamma^\mu = 0}$$が示せるのだ。なので、電荷は一様重力の外力のみを受けるので、電荷なしの物体と同じ加速度で落ちる、ということである。この$${\Gamma^\mu = 0}$$が問題なのである。電磁波を放射する以上、狭義の反作用項である上記$${\Gamma^\mu}$$の第2項は本来ゼロではあり得なそうだが、その場合、第1項とキレイに相殺するのはどういうカラクリか?というのが長年問題らしく、未だ統一的な理解はないようである。まあ、この放射の反作用関連は、式42自体の妥当性も議論のあるところなので、古典論に限定してあまり深堀しても意味がないような気がする。
冒頭に述べた疑問から始まって、昨年の夏くらいから隙間時間に一般相対論を復習しつつリンドラー時空を巡る旅をして来て、その奥深い世界を堪能できたが、ここで一区切りである。リンドラー時空は、量子力学も絡めると、ウンルー効果やホーキング輻射など、ブラックホールの物理にも関連するようで、その奥深い世界はまだまだ続くようである(数理科学2024年1月号の西岡辰磨氏の記事「量子情報理論とブラックホールの物理」にもリンドラー座標が出てくる)。これらについて理解するのは、宿題としてとっておく。
この記事が気に入ったらサポートをしてみませんか?
