はじめに

　等加速運動を相対論的に記述するリンドラー座標について、これまでに以下の3篇の記事を書いた。

①リンドラー座標を自力で導出してみた―等加速度運動の相対論的記述―
②リンドラー座標つれづれ(1)―双子のパラドックス―
③一般相対論的放物線―リンドラー座標つれづれ(2)―

相対論的な等加速度運動で興味深いのは、等加速度運動する主体が荷電粒子の場合である。荷電粒子の等加速度運動を相対論的に取り扱うと、荷電粒子自身が周囲に作る電磁場や、荷電粒子が放射する電磁場について、古典電磁気学に基づく素朴な予想と合わない結果が出てくる。この辺は大学の物理学科の授業でもほとんど触れられることがなく、電磁気学の教科書にもほとんど載ってないので、物理学を学んだ人でも知っている人は少ないのではないだろうか。本稿で紹介するのは、ガウスの法則の破綻（？）である。

ガウスの法則とは、ざっくり言えば、空間に任意の閉曲面を設定したとして、同時刻に閉曲面から出る正味の電場を積分すると、閉曲面内部に存在する電荷の和に等しくなる、というものである。閉曲面を、点電荷を中心とする球面に設定すれば、高校の物理でも習うクーロンの法則が直ちに導出できる。この法則はマクスウェル方程式の1つで、真空中の場合の表式は、微分形、積分形それぞれ、

$${\displaystyle \nabla\cdot\bold E = \frac{\rho}{\varepsilon_0}}$$　式1

$${\displaystyle \iint_{S} \bold E \cdot d\bold S = \frac{1}{\varepsilon_0}\iiint_V \rho \,dV}$$　式2

となる（この記事を読むような方には、記号の意味の説明は不要でしょう）。さて、この法則は、閉曲面内に存在する電荷の運動状態に依らず（加速度運動していても）成立するのだが、以下に見るように、電荷が一様に等加速度運動している場合、閉曲面の設定の仕方によっては（一見）破綻する場合があるのである。

等加速度系に現れる事象地平面

ガウスの法則の破綻の話の前に、リンドラー座標系に現れる事象の地平面について議論する。ここで、復習。静止系（S系）に対して、$${x}$$方向に一定の加速度$${a'}$$で動いている座標系をS'系とすると、S'系の座標$${(t', x')}$$とS系の座標$${(t, x)}$$の間の相対論的な変換式は、

$${\displaystyle t = \frac{1}{a'} e^{a'x'} \sinh a't'}$$　式3

$${\displaystyle x = \frac{1}{a'} e^{a'x'} \cosh a't'}$$　式4

で与えられる（リンドラ―変換）。今の場合、$${t = t' = 0}$$のとき、S'系の原点のS系における位置は、$${x = 1/a'}$$である。図示すると、以下のようになる。

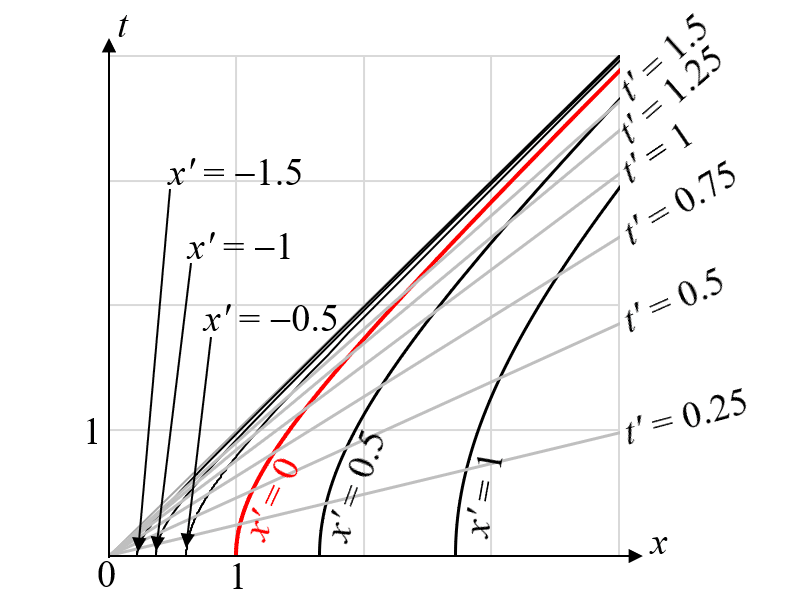
$${x'}$$が一定の軌跡は、$${tx}$$空間では双曲線を描く。$${t'}$$が一定の軌跡は、すべて原点を通る直線となる。$${x' \to -\infty}$$あるいは$${t' \to\infty}$$のいずれの極限でも、光速度の軌跡$${t = x}$$の直線に収束する。

図示すると上述の通りなのだが、よく考えてみると、なかなか奇妙なことが起きている。等加速度系S'に乗っている観測者から見ると、任意の時刻$${t'}$$において、空間は前方にも後方にも無限に広がっている（$${-\infty < x' < \infty}$$）ように見えるはずであるが、後方の座標は、どんなに遠方でも、静止系Sでは原点$${x=0}$$に収束してしまい、$${x \leq 0}$$の範囲には行くことができない。$${x = 0}$$の位置が、S'系にとってはあたかもブラックホールの事象の地平面と同様の振る舞いをしている。

リンドラー座標系の事象の地平面について、もうちょっと詳しく見てみよう。ブラックホールの事象の地平面の場合、地平面内部からは光さえも出ることができないので、地平線内部の様子は、地平線外部からは全く知ることができない。一方、リンドラー座標系の事象の地平面は、その意味がやや異なる。

静止系Sにいる観測者が、等加速度運動する観測者（リンドラー観測者）に光で情報を送る場合を考えよう（下図）。

静止系観測者は、$${x = -2}$$の位置に留まっているとする（上図の太い青線）。リンドラー観測者は、無限過去の無限遠点からやってきて、$${t = 0}$$で$${x = 1}$$の位置で反転し、無限未来の無限遠点に向かっていく（上図の赤線）。上図に示したように、発信時刻が$${t < x}$$ならば、リンドラー観測者は、$${x \leq 0}$$にいる静止系観測者が発した光を受信することができるが、$${t \geq x}$$となると見えなくなる。リンドラー観測者から見ると、時刻$${t'}$$の経過に従って、静止系の景色は$${t\to x}$$に向かって時が止まっていくように見えるはずである。

では逆に、リンドラー観測者観測者が静止系観測者に向かって光を送るとどうなるか？（下図）

この場合、図2とは上下反転して、静止系観測者は、$${t \leq -x}$$のとき、リンドラー観測者の存在を感知できないが、$${t > -x}$$になると受信できるようになる。リンドラー観測者が無限過去から連続して光を後方に送信している場合、静止観測者は、$${t = -x}$$の瞬間に突然光を受信することになる。一方、リンドラー観測者から見ると、後方に発した光が無限の彼方に消えていくだけで、静止系観測者と情報をやりとりすることはできない。

上記の話は、2つの座標系にいる観測者が、互いに相手に向かって光を発したとき、それを観測できる／できないの境界線が生じるというものであるが、リンドラー観測者を荷電粒子に置き換えると、奇妙なことが起きる。図3の、リンドラー観測者が出す光は、等加速度運動をする荷電粒子が周囲に形成する電磁場に置き換えることができる。すると、静止系観測者から見た場合、その電磁場は、ある時刻から突然不連続に発生するように見える。言わば、荷電粒子が形成する電磁場の「端」が観測できてしまい、その「端」を跨ぐように閉曲面を設定すると、ガウスの法則が簡単に破綻しまう（ように見える）のである。以下で、厳密に計算してみてみよう。

等加速度運動をする荷電粒子が形成する電磁場

この問題を考えるには、加速度運動する点電荷が形成する電磁場の一般式が出発点となる。上記までは光速度$${c=1}$$とする単位系で表現していたが、以下で光速度は$${c}$$に戻す。

電磁場の一般式

運動する点電荷$${q}$$があり、その位置を$${\bold{r}_s}$$，速度を$${\boldsymbol v}$$で表す。この点電荷の電磁場を位置$${\bold{r}}$$，時刻$${t}$$で観測する状況を考える（下図）。

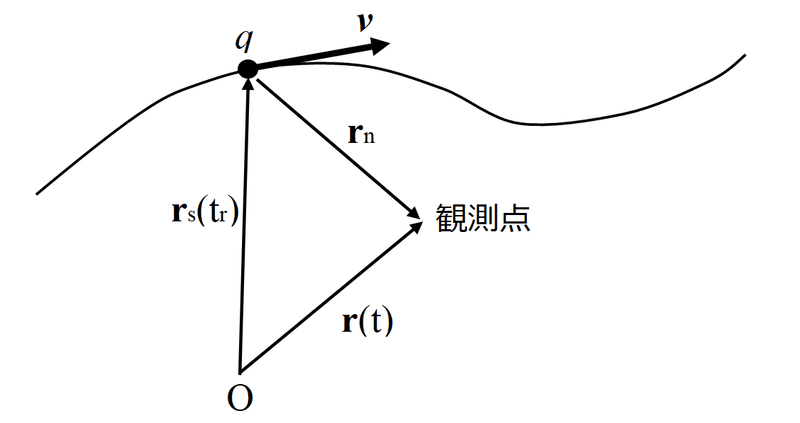
ここで、$${\bold r_n}$$は、

$${\bold r_n = \bold r - \bold r_s}$$　式5

で定義され、$${\bold r_s}$$，$${\bold v}$$は、次式で与えられる遅延時刻$${t_r}$$における値である。

$${t_r=t - |\bold r(t) - \bold r_s(t_r)|/c = t - r_n /c}$$　式6

このとき、位置$${\boldsymbol r(t)}$$における電磁場は、よく知られた面倒な計算（たとえばグリフィス「電磁気学II」を参照）を経て、以下の式で与えられる。

$${\bold E(\bold r, t) = \dfrac{q}{4\pi\varepsilon_0}\dfrac{r_n}{(\bold r_n\cdot\bold u)^3}\left\{(c^2-v^2)\bold u+\bold r_n\times(\bold u \times \bold a) \right\} }$$　式7

$${\bold B(\bold r, t) = \dfrac{1}{c}\bold{\hat r} _n \times \bold E(\bold r, t)}$$　式8

ここで、$${\bold a = \partial \bold v/\partial t}$$は点電荷の加速度であり、$${\bold u}$$は$${\bold u=c\bold{\hat r}_n - \bold v}$$（$${\bold{\hat r}_n}$$は$${\bold r_n}$$方向の単位ベクトル）で定義される。繰り返すが、右辺に現れる速度$${\bold v}$$, 加速度$${\bold a}$$は、遅延時刻$${t_r}$$における値であることに注意。

※余談だが、式7, 8は、運動する電荷が生成する電磁場を与える一般式で、言わば、古典電磁気学の集大成的な表式なのだが、大学学部レベルの電磁気学の授業ではそこまで到達しないことが多いので、物理学徒でも意外と知らない人が多いのではないだろうか（物理で博士号を取った自分でも、2年前にグリフィスの教科書を読んで初めて知ったのだが）。

等加速度運動の場合

さて、図2, 3の赤線のように、荷電粒子が等加速度運動する場合に形成される電場を、式7を用いて計算してみよう。ここからは、以下の論文を参照した。著者に、前述の教科書のグリフィスが入っている。

J. Franklin & D. J. Griffiths, 2014. The fields of a charged particle in hyperbolic motion. American Journal of Physics, 82(8): 755-763.

荷電粒子は$${z}$$軸上を移動するものとする。$${t = -\infty}$$, $${z = +\infty}$$から原点に向かって移動してきて、$${t = 0}$$に$${z = b\,\,(>0)}$$に到達し、そこで折り返して$${t = +\infty}$$, $${z = +\infty}$$に向かって飛び去って行く。電荷の位置$${z}$$は、

$${\displaystyle z(t) = \sqrt{b^2+ (ct)^2}}$$　式9

と書ける。観測点（$${xz}$$平面上にとる）と、遅延時刻における電荷の位置ベクトルはそれぞれ、

$${\displaystyle \bold r  = x \bold{\hat x}+z\bold{\hat z} \\ \bold r_s = z(t_r) \hat{ \bold z}}$$

であるので、$${\bold r_n}$$は、

$${\displaystyle \bold r_n  = x \bold{\hat x}+\left\{z-\sqrt{b^2+(ct_r)^2}\right\}\bold{\hat z}}$$　式10

となる。また、速度と加速度は、次式で与えられる。

$${\displaystyle \bold v = \frac{d\bold r_s}{dt} = \frac{c^2t_r}{\sqrt{b^2+(ct_r)^2}}\hat{\bold z}}$$　式11

$${\displaystyle \bold a = \frac{d\bold v}{dt} = \frac{c^2b^2}{\left\{\sqrt{b^2+(ct_r)^2}\right\}^3}\hat{\bold z}}$$　式12

遅延時刻$${t_r}$$を求めよう。以下で、電荷が$${t = 0}$$で折り返し地点に来た時の電場を求めることにするので、式6より、

$${ct_r = -r_n\,\,(< 0)}$$　式13

となる。式10より、

$${\displaystyle (ct_r)^2 = r_n^2 = x^2 + \left\{ z - \sqrt{b^2+(ct_r)^2} \right\} \\ \, \\ \quad = x^2+z^2-2z\sqrt{b^2+(ct_r)^2}+b^2+(ct_r)^2}$$

となり、これを解いて、

$${\displaystyle ct_r = -\frac{1}{2z}\sqrt{\left( x^2 + z^2 + b^2\right)^2-(2bz)^2}}$$　式14

となる（$${t_r<0}$$であることに注意）。

以上の材料を式7に代入して、$${t = 0}$$における電場を求める。けっこう面倒な計算を経て、

$${\displaystyle \bold E = \frac{qb^2}{\pi\varepsilon_0}\frac{(z^2-x^2-b^2)\hat{\bold z} + 2xz \hat{\bold x} }{ \left\{\sqrt{\left(z^2+x^2+b^2 \right)^2-\left(2zb \right)^2} \right\}^3 }  }$$　式15

を得る。この電場は、$${z}$$軸の周りで回転対称なので、上式の$${x}$$は$${z}$$軸からの距離で読み換えても良い。この表式では、$${z}$$軸上で$${z=\pm b}$$の2点が特異点になっているだけで、$${z = 0}$$でも電場は連続であるが、上述のように、実際には異なる。図3に示したように、原点にいる観測者は$${t = 0}$$に突然電場を感じるようになり、しかもその瞬間においては、$${z < 0}$$で電場はまだゼロである。従って、$${t = 0}$$における電場は、正しくは式15に階段関数$${\theta(z)}$$を掛けたものとなる。図示すると以下のようになり、$${z = 0}$$において電気力線がプッツリと切れ、電場の「端」が露わになる。

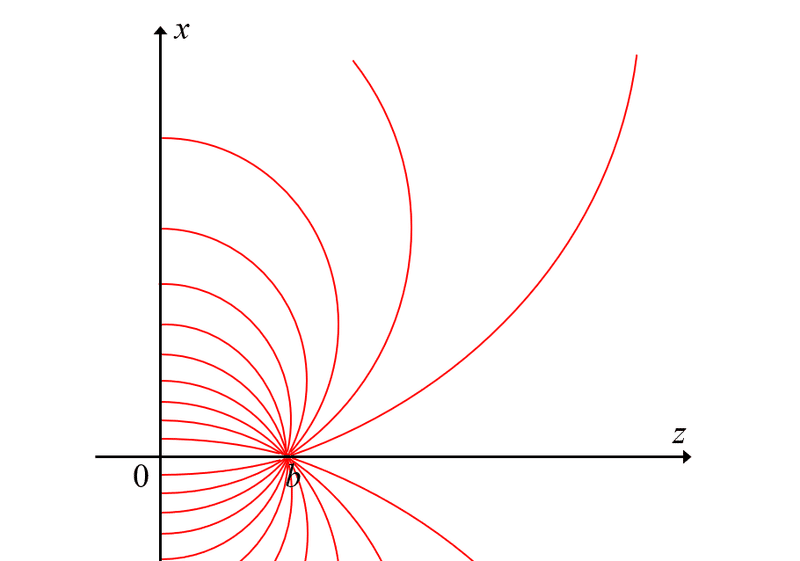
境界面のプラス側ギリギリのおける電場は、式15で$${z = 0}$$として、

$${\displaystyle \bold E(z = 0^+) = -\frac{qb^2}{\pi\varepsilon_0}\frac{\hat {\bold z}}{(s^2+b^2)^2}}$$　式16

となる（$${s}$$は$${z}$$軸からの距離）。電場は境界面において$${z}$$軸に平行である。

さて、$${z = 0}$$の境界面をまたぐように閉曲面を設定して電場の表面積分を求めるとどうなるか？$${z}$$軸のまわりに半径$${R}$$の円盤（厚さ無限小）を設定すると、積分に寄与するのは$${z = 0^+}$$側の底面のみであるので、

$${\displaystyle \iint \bold E \cdot d\bold S = -\frac{qb^2}{\pi\varepsilon_0}\int_0^R\frac{2\pi s}{(s^2+b^2)^2}ds \\ \, \\ \quad = -\frac{q}{\varepsilon_0}\frac{R^2}{R^2+b^2}}$$　式17

となった！この閉曲面内には電荷が存在しないにも関わらず、積分はゼロにならないのである。

ガウスの法則は本当に破綻？

上記の結果そのままでは、ガウスの法則が破綻することになるのだが、実は、この問題には続きがある。注意深く計算すると、図5に示した電場は実は正しくなく、$${z = 0}$$の境界面上で、z軸を中心に外向きに出る電場がデルタ関数的に付け加わったのが正しい姿となる（らしい）。この場合、式17の積分に動径方向の電場も寄与するので、その結果、積分値はちゃんとゼロになる（らしい）。その部分に関する議論も上記の論文に載っているのだが、式展開に誤りがあり、その後、別の論文で正しい電場の導出が示されている。その後さらに、技巧的な式展開に依らない直観的な導出方法を示した論文も出ている。この辺については、まだ理解が追い付いていないので、稿を改めて紹介する。いずれにしても、19世紀後半に確立した古典電磁気学だが、こんな単純で分かりやすい問題に関して、21世紀のつい最近まで議論が続いていたのだ。古典電磁気学の何と奥深いことか！

2024.02.11追記。解決編はこちら↓