はじめにご了承いただきたいのは，この記事を執筆したのは文学部最弱の学生だということです．間違っている部分があるかもしれません．間違いを見つけた場合には，是非ともコメントで教えてくださいね．温かい目で読んでください．
　あ，それとこの記事はTeX記法の練習も兼ねてます．アルゴリズムの説明をする節はTeX記法使っちゃいました．大人になった気分です．

アルゴリズムの説明

　MCMCの過程に関しては，ちゃんとした参考書やサイトを読んでもらえればいいと思います．ここでは簡単な説明で済まします．

　成功回数を$${y}$$，失敗回数を$${z}$$，成功確率を$${k}$$とすると，負の二項分布の確率質量関数は，

$${f(z) = {}_{y+z-1}C_zk^z(1-k)^y}$$

となります．今回は成功回数は1なので，

$${f(z) = {}_zC_zk^z(1-k)=k^z(1-k)}$$

です．残ったパラメータは$${z}$$と$${k}$$です．$${z}$$は実現値を見ればわかるので，実質的に不明なパラメータは$${k}$$のみです．この$${k}$$をMCMCサンプリングで推測します．
　まずは適当にパラメータ$${k}$$の初期値を用意しておきます．ただし$${k}$$は確率なので0以上1以下である必要があります．今回は$${k=0.9}$$と設定しておきました．とくに理由はありません．
　$${k=0.9}$$であるときの実現値$${x^n}$$の生起確率（のようなもの）$${p(x^n|k=0.9)}$$を求めます．
　今回実装に使うのは感染症の二次感染の度数を簡略化したものです（以下）．

#二次感染者数を簡略化したもの．
observed = [25 , 5 , 2 , 0 , 0 , 0 , 1]

　感染を広めなかった人（0人に感染を広めた人）は25人．1人に広めた人は5人．2人に広めた人は2人．3，4，5人に広めた人は0人．6人に広めた人は1人として分析を行います．
　さて，$${p(x^n|k=0.9)}$$は次の式に$${k=0.9}$$を代入すると求まります．

$${p(x^n|k)=\prod_{i=1}^{25}k^0(1-k)×\prod_{i=1}^5k^1(1-k)×…×\prod_{i=1}^1k^6(1-k)}$$

これを計算すると，0.03815204244769461が得られます．長いですね．これが初期パラメータの下での実現値の生起確率です．
　続いて0以上1以下の乱数をひとつ発生させます．それを新しい$${k}$$の値として提案します．
　ここでちょっと$${k}$$の表記を変えます．もともとあるパラメータ$${k}$$を$${k_0}$$，新しく提案された$${k}$$を$${k_1}$$とします．
　そして

$${r=\dfrac{p(x^n|k_1)p(k_1)}{p(x^n|k_0)p(k_0)}}$$

を計算します．今回は$${k_0}$$と$${k_1}$$は同じ一様分布からサンプリングされるとしているため，$${p(k_0)}$$=$${p(k_1)}$$です．ゆえに，

$${r=\dfrac{p(x^n|k_1)}{p(x^n|k_0)}}$$

と変形できます．
　分母はもともとあるパラメータの下での実現値の生起確率．分子は提案されたパラメータの下での実現値の生起確率です．（コードではoddsとしています）
　$${r}$$が1よりも大きければ，$${k_1}$$は$${k_0}$$よりもパラメータとしてふさわしいとみなし，それを次世代のパラメータとして採用します．
　$${r}$$が1よりも小さければ，確率$${r}$$でパラメータ$${k_1}$$を採用し，確率$${1-r}$$でパラメータ$${k_0}$$を残します．
　採択されたパラメータは次のステップでは$${k_0}$$となり，次に発生させた乱数（$${k_1}$$）と再び比較されます．ドミノ倒しみたいなイメージでしょうか．
　これを繰り返して，採用されていくパラメータの挙動を観測します．
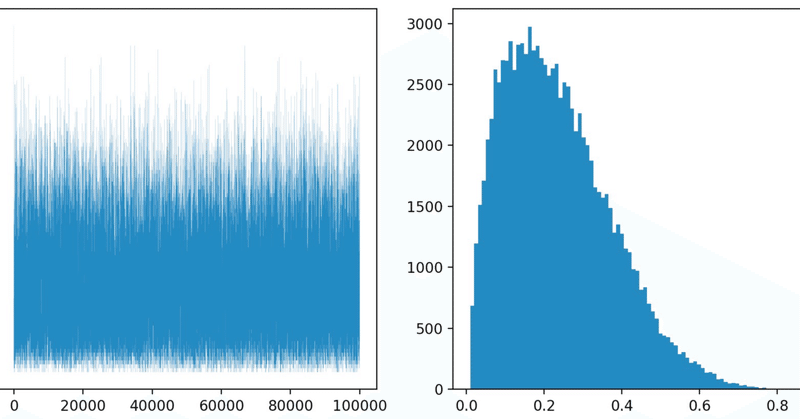
　説明はこれくらいにして実際にコードを走らせてみましょう．走らせた結果が下の図です．

　トレースプロットを見てみましょう．これは採択された$${k}$$の挙動を表したものです．最初は$${k=0.9}$$から始まったのですが，その後は0.1から0.4に集中しているのが分かります．ごちゃごちゃして見にくいかもですがね．
　ヒストグラムは採用された$${k}$$の頻度を表したものです．0.2あたりで盛り上がりが最大になっていますね．ちなみに平均値0.23ほどに落ち着きます．
　MCMCでは最初の数千回ループをバーンイン（挙動が不安定になっている可能性があるため切り捨てる）することがあるようですが，面倒だったので今回はしていません．バーンインしたとしても結果はそんなに変わらないと思います．バーンインが関係ないくらいの試行回数を踏んだと思っていますし．

　最後に実際のPythonのコードを載せておきます．参考になれば幸いです．

Pythonのコード

　えっとですが，ちょっとコードでは

$${f(z) = {}_zC_z(1-k)^zk=(1-k)^zk}$$

というカタチになっています．
　ミスってしまっていますが，直すのが面倒なので放っておきます．

from itertools import product
import numpy as np
import matplotlib.pyplot as plt
from statistics import mean, stdev, variance

#二次感染者数を簡略化したもの．
observed = [25 , 5 , 2 , 0 , 0 , 0 , 1]

#提案される乱数kのリストを先に作っておく．
propose_k= []
#ステップ数
steps = 100000
#小数第2位までの乱数を生成し，リストに追加する．
for a in range(steps):
    k = round(np.random.uniform(0 , 1) , 2)
    propose_k.append(k)


#kの関数を定義．負の二項分布のパラメータがkのとき，実現値が生起する確率を算出．
def f(k):
    for b in range(len(observed)):
        #失敗確率のb乗と成功確率の積をとっていく．その都度リストに数値を追加していく．
        prob_b = (1-k)**(b)*k**observed[b]
        prob_list = []
        prob_list.append(prob_b)
        #リストの要素の総積をとり，それをパラメータkの下での生起確率とする．
        prob_k = np.product(prob_list)
    #リストの中身を全部削除する．リセットして次に備える．
    prob_list.clear()
    return round(prob_k , 2)



#パラメータkのためのリストを作成．初期値を入れておく．0.9にしておく．理由はない．
para_k = [0.9]
#MCMCの過程で選択されたパラメータkの下での実現値生起確率のリストを作成．初期値はf(0.9)．
prob_MCMC = [0.03815204244769461]

#MCMC M-H
for c in range(len(propose_k)):
    odds = f(propose_k[c]) / prob_MCMC[c-1]
    #オッズが1より大きいか小さいかで条件分岐
    #オッズが1よりも大きいときは提案されたパラメータの方がふさわしいという意味
    if odds > 1:
        para_k.append(propose_k[c])
        prob_MCMC.append(f(propose_k[c]))
    else:
        rand = np.random.uniform(0,1)
        #乱数を発生させて，新しいパラメータを採択するかどうかを判定する．
        if odds > rand:
            para_k.append(propose_k[c])
            prob_MCMC.append(f(propose_k[c]))
        else:
            para_k.append(para_k[c])
            prob_MCMC.append(prob_MCMC[c-1])

#平均値を求め，描画

fig = plt.figure()
ax1 = fig.add_subplot(1,2,2)
ax1.hist(para_k , bins = 90)
ax2 = fig.add_subplot(1,2,1)
ax2.plot(para_k, lw = 0.05)
plt.show()

インプリケーション

　今回サンプリングした$${k}$$とは何を表しているのかということですが，これは感染を広めない確率みたいな解釈ができるのではないでしょうか？
　つまり0.23くらいの確率で感染者は感染を他の人に広めません．裏を返せば，0.67ほどの確率で感染を誰かに移すということがいえます．

まとめ

　本当はPythonでPyMCだったか忘れましたが，MCMCをやってくれるやつがあるとかないとかですが，やり方が分からず「これなら自分でコード組んだ方が早いわ！」ってことでこういう記事を作りました．
　ここで扱った成功回数が1回の負の二項分布のMCMCは，競馬の予想なんかでも応用できそうです．度数のグラフ作ったときに左から右にかけて背が低くなっていくものには使えるかなって．競馬は1番人気が一番勝つ傾向にあり，2番人気，3番人気と次いで勝利する傾向にあると思います．
　まあなんというか，競馬はレースによって出走馬が異なりますし，馬場状態や気温天気も日によって違いますよね．だからサンプリングされた標本が独立同分布からであるという仮定が置きにくくて，データ分析をするのはちょっと無理があるような気がしていますが．
　ここまで書いてみましたが，競馬はその時々の好みや直感で楽しむくらいがちょうどいいですね．下手にデータ分析で予想して外したら自信喪失してしまいそうやし……．
　というわけでここらへんでドロンします．
　間違っているところたくさんあるかもしれませんが，いつか誰かの参考になればいいなって思います．
　さらば！