表現論に関する書籍を読んだら、しっかり記録をとるようにしたいと思います。さっそくですが、『線形代数と群の表現 I』（平井武 著）のp.14にある問題1.3について解答案を作成しました。群における$${n}$$個の元の演算結果は、結合律により括弧の付け方に依存しないという、ほぼ自明なものです。なぜか平井先生の本では「やや難」とされていました。

それほど難しい問題なのか、その辺は私には分かりませんが、自分なりに解答案を作成しました。解答のアイディアの根幹は田中一之先生の本『チューリングと超パズル』にある「数学のセンスを判断するパズル」です。そのことについても後半に書きました。

群におけるn個の元の結合

『線形代数と群の表現 I』で出題されている問題は次のものです。

問題1.3　群$${G}$$において$${n}$$個の元の結合のさせ方は
$${a_1(a_2(a_3\cdots(a_{n-1}a_n)\cdots))}$$（右側から順番に掛ける）に等しいことを、$${n}$$に関する数学的帰納法で示せ。

私はこれに対して、次のように解答案を作成しました。

証明
$${n=1,2}$$のときは自明。よって$${n\ge3}$$に対して考えればよい。
[1]　$${n=3}$$のとき、群の結合律より$${(a_1a_2)a_3=a_1(a_2a_3)}$$であるから成り立つ。

[2]　$${n\le k}$$のとき成り立つことを仮定し、$${n=k+1}$$のときにも成り立つことを示す。

まず$${k+1}$$個の元を結合する順番を、括弧の付け方で完全に指定することはできないが、最後に結合する箇所は指定できることを確認する。
例えば$${n=4}$$のとき、$${(a_1a_2)(a_3a_4)}$$と書かれた式は、$${(a_1a_2)}$$と$${(a_3a_4)}$$のどちらを先に結合させるのかは指定されていない。しかし、いずれを先に結合させるにしても、最後に結合させるのは$${(a_1a_2)}$$の結合結果と$${(a_3a_4)}$$の結合結果である。

よって、$${k+1}$$個の元の最後に結合する箇所が左から$${l}$$個目の結合箇所であるとして証明をする。$${k+1}$$個の元には$${k}$$個の結合箇所があるから、$${l}$$は$${1\le l\le k}$$を満たす自然数である。
例えば$${n=4}$$のとき、$${a_1(a_2(a_3a_4))}$$に対して$${l=1}$$である。$${(a_1(a_2a_3))a_4))}$$に対して$${l=3}$$である。

[2-i]　$${l=1}$$のとき、結合の仕方は次のようになっている。

$$
a_1\times(a_2,\ldots,a_{k+1}の結合)　①
$$

ただし分かりやすさのために、群の二項演算の記号に$${\times}$$を使用した。
ここで①の$${(a_2,\ldots,a_{k+1}の結合)}$$の部分は$${k}$$個の元の結合であるから、帰納法の仮定により

$$
a_2(a_3(a_4\cdots(a_ka_{k+1})\cdots))　②
$$

に等しい。
よって、①、②より$${k+1}$$個の元の結合は

$$
a_1(a_2(a_3(a_4\cdots(a_ka_{k+1})\cdots)))
$$

に等しい。

[2-ii]　$${2\le l\le k}$$とき、結合の仕方は次のようになっている。

$$
(a_1,\ldots,a_lの結合)\times(a_{l+1},\ldots,a_{k+1}の結合)　③
$$

ここで$${(a_1,\ldots,a_lの結合)}$$の部分は$${l}$$個の元の結合であり、$${l\le k}$$であるから帰納法の仮定により、$${a_1(a_2(a_3\cdots(a_{l-1}a_l)\cdots))}$$に等しい。

$${a_2(a_3\cdots(a_{l-1}a_l)\cdots)}$$を$${x}$$とおく。さらに③の$${(a_{l+1},\ldots,a_{k+1}の結合)}$$の部分を$${y}$$とおく。③は次に等しい。

$$
(a_1x)y
$$

これは結合律から$${a_1(xy)}$$に等しい。よって$${l=1}$$の場合に帰着できる。

[2-i]、[2-ii]より、$${n=k+1}$$のとき成り立つことが示せた。

したがって、[1]、[2]より、任意の$${n}$$に対して$${n}$$個の元の結合のさせ方は
$${a_1(a_2(a_3\cdots(a_{n-1}a_n)\cdots))}$$に等しいことが示せた。
（証明終）

数学のセンスを判断するパズル

この証明の[2-i]と[2-ii]の部分は『チューリングと超パズル』（田中一之 著）のpp.9-13を参考にしました。そこには「数学のセンスを判断するパズル」として次のような問題が書かれています（元はガードナーの問題集が出典だそうです。また、以下の文章はいろいろ改変しています）。

問題1　ある日、あなたはある公園に南側の入り口から入りました。公園を見渡すと東側のゴミ箱から炎が上がっていました。公園の中央には空のバケツが転がっており、北側には水道の蛇口があります。さて、あなたはどうしますか？

これは簡単な問題でほとんどの人が次のように解答すると思います。

問題1の解答例
(1)公園の中央へ行ってバケツを拾い、(2)北側の水道でバケツに水を入れ、(3)東側へ行って炎が出ているゴミ箱に水をかける。
炎が消えれば終了。消えなければ消えるまで(2)と(3)を繰り返す。（終）

本題は次です。

問題2　別の日、あなたはその公園にまた南側の入り口から入りました。東側のゴミ箱からこの日も炎が上がっていました。公園の中央には水が入ったバケツが置いてあります。さて、あなたはどうしますか？　数学的にエレガントな解答を考えてください。

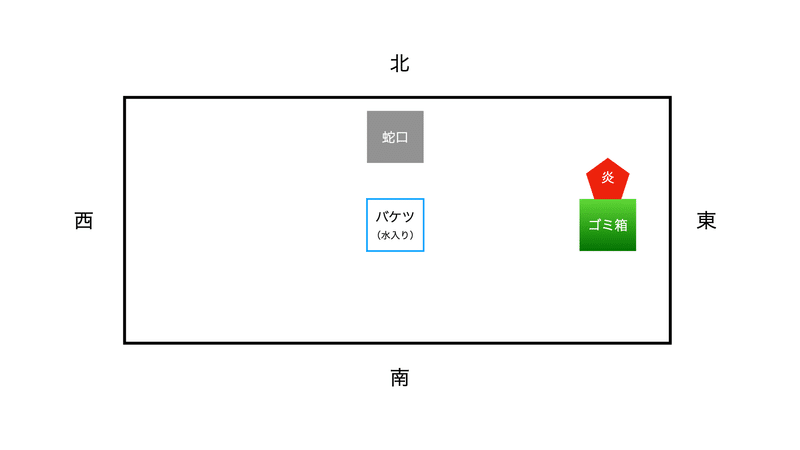
問題2の解答例
公園の中央まで行ってバケツを蹴飛ばして空にし、公園の入り口に戻る。これで問題1と同じ状況になったので、あとは問題1の解答例と同じ。（終）

野暮ですが敢えて解説すると、現実世界でこの問題2の解答例と同じことを実行するのはナンセンスです。しかし、数学の問題の解答としては、すでに解いた問題1の解答に帰着させるという点で省エネであり、エレガントな解答と言えます。

数学の問題を考える際、このような戦略をとることはよくあるように思います。ただし、せっかく水が入った状態のバケツがあるのに蹴飛ばしてしまうほどの虚無的行動が必要になることはほとんどないと思います。多分。

（おしまい）

参考文献

• 平井武 著、『線形代数と群の表現 I』、2001

• 田中一之 著、『チューリングと超パズル』、2013