行列のジョルダン標準形を求めていたら、線形代数の初歩的なことについて自分が勘違いをしていることに気づきました。それについて私が実際に行った計算の画像を貼って説明します。

問題の行列

先日、私は以下の行列$${A_1}$$のジョルダン標準形を求めようとしていました。

以前のnoteの方法を使いました。なお、$${A_1}$$は筧 三郎 著『工科系 線形代数［新訂版］』（数理工学社、2014）のp.153にあるものです。

まずは固有多項式を求める

初手で固有多項式$${\phi_{A_1}(x)=\det(xE-A_1)}$$を求めます。
最初は愚直に計算しようと思いましたが、途中で$${x-2}$$を因数に持つことに気づき、やり直しました。以下のバツの部分はその跡です。

$${A_1}$$の3列目から2列目を引き、$${x-2}$$を括り出してから行列式を計算しました。$${\phi_{A_1}(x)=(x-2)(x-3)^2}$$であり固有値は2と3であると分かりました。

ジョルダン標準形の型を突き止める

固有多項式が分かると、ジョルダン標準形は対角行列か右上に1箇所だけ1が現れる型のどちらかに絞られます。

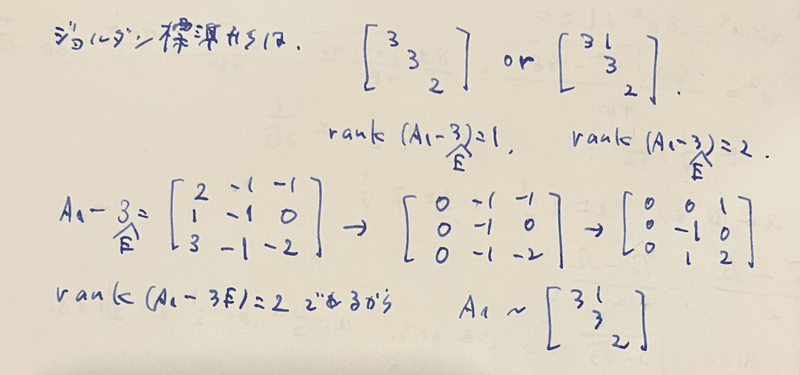
さらに$${\mathrm{rank}(A_1-3E)=2}$$から、右上に1箇所だけ1が現れる型の方であると分かりました。
以前のnoteの方法の3次の②の2番目の方法でやればいいようです。

固有値3の一般固有空間の基底を求める

ジョルダン標準形の型は分かったので、次に一般固有空間の基底を求めました。その際には最小多項式$${\psi_{A_1}(x)}$$を利用しました。今回は$${\psi_{A_1}(x)=\phi_{A_1}(x)}$$です。

$${(A_1-3E)^2(A_1-2E)=0}$$より、$${A_1-2E}$$の列ベクトルに固有値3の一般固有空間の基底が隠れています。
画像中には書いていませんが$${\mathrm{rank}(A_1-2E)=2}$$です。よって1次独立なベクトルが2個とれます。
上手にとれば、$${\ker(A_1-3E)^2\backslash\ker(A_1-3E)}$$から1個、$${\ker(A_1-3E)}$$から1個とれます。
以下の画像中の4行目のように、$${A_1-2E}$$の1列目$${\begin{bmatrix}3\\1\\3\end{bmatrix}}$$に$${A_1-3E}$$を掛けると、$${\begin{bmatrix}2\\2\\2\end{bmatrix}}$$となります。

これで、$${\begin{bmatrix}3\\1\\3\end{bmatrix}\in\ker(A_1-3E)^2\backslash\ker(A_1-3E)}$$、$${\begin{bmatrix}2\\2\\2\end{bmatrix}\in\ker(A_1-3E)}$$であると分かりました。
多少、整えて$${\begin{bmatrix}1\\0\\1\end{bmatrix}\in\ker(A_1-3E)^2\backslash\ker(A_1-3E)}$$、$${\begin{bmatrix}1\\1\\1\end{bmatrix}\in\ker(A_1-3E)}$$としておきます。

固有値2の固有ベクトルを求める（私の勘違い）

最後に固有値2の固有ベクトルを求めますが、ここで私は初歩的な勘違いをしてしまっていました。てっきり$${\begin{bmatrix}1\\0\\1\end{bmatrix},\begin{bmatrix}1\\1\\1\end{bmatrix}}$$と直交する$${\begin{bmatrix}1\\0\\-1\end{bmatrix}}$$をとればいいと思っていたのですが、それは間違いでした。
$${\R^3=\ker(A_1-3E)^2\oplus\ker(A_1-2E)}$$と直和分解されますが、これは直交直和ではないのに、直交直和であると思い込んでいました。
以下の画像のバツの部分のようにしてしまいましたが、
$${\begin{bmatrix}1\\0\\-1\end{bmatrix}\neq\ker(A_1-2E)}$$でした。

正しくは、$${\begin{bmatrix}1\\1\\1\end{bmatrix}\in\ker(A_1-3E)}$$とは独立な$${A_1-3E}$$の列ベクトル、1列目か3列目に$${A_1-3E}$$を掛ければよかったのです。3列目である$${\begin{bmatrix}-1\\0\\-2\end{bmatrix}}$$に$${A_1-3E}$$を掛けると$${\begin{bmatrix}0\\-1\\1\end{bmatrix}}$$が得られ、これは固有値2の固有ベクトルです。

ジョルダン標準形を得た

以上、四苦八苦しましたが、次のようにジョルダン標準形に変形するための基底を得ることができました。

まとめ

• 筧先生のテキストにある行列のジョルダン標準形を求めることができました。

• 以前のnoteの方法でできました。

• しかし、一般固有空間への直和分解に関して勘違いをしており、最初ミスりました。

• 次から気をつけようと思いました。

（おしまい）

参考文献

筧 三郎 著『工科系 線形代数［新訂版］』（数理工学社、2014）