論文要約

この論文では、高いコストでデータを収集することが難しい状況において、少ないデータからも有効な結論を導き出す新しいアプローチについて説明しています。具体的には、物理学や生物学などの分野で既に知られている知識（事前知識）を活用することで、機械学習モデルの精度を向上させる方法を探求しています。

この研究の核となるのは、「物理情報を組み込んだニューラルネットワーク」という技術です。これは、物理法則を尊重しながら学習するニューラルネットワークを開発することにより、限られたデータからでも効率的に学習し、正確な予測を行うことができるようにするものです。

この技術を用いることで、計算科学の問題を解決する新しい方法が提供され、偏微分方程式を解く新しい数値解法や、データから直接物理モデルを学習する方法が開発されます。これにより、科学的研究だけでなく工業応用においても、データを効果的に活用し、より良い意思決定を行う支援が期待されます。

今回の目的

論文では2次元(x, t)の偏微分方程式を解いているが、それを3次元に拡張することが可能かどうかを検証します。また、次元数の増加に伴う学習時間の変化を集計することによって、実際に運用可能かどうかを検証します。

環境と環境構築

Python == 3.6.8
TensorFlow == 1.15.3

今回はTensorFlowのバージョン1(TF1)を使ってプログラム実装
TF1はPython3.6でしか動かないので、まずはPython3.6.8をインストール
Numpy, Scipy, matplotlib, pyDOEはPyPI(pipコマンド)からインストール

前提条件

今回は拡散方程式を解く。
拡散方程式は
𝑢𝑡−(𝑢𝑥𝑥+𝑢𝑦𝑦)=0
初期条件は以下のGaussianを採用する。
𝑢(𝑥,𝑦,0)=𝑒𝑥𝑝(−(𝑥2+𝑦2))

Gaussianは以下のような局所的な解になっている。

#Data generation-----------------------------------
xi = np.linspace(-5, 5, 100)
yi = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(xi, yi)
ui = np.exp(-(X**2 + Y**2))

tti = np.zeros(10000)[:,None]
xxi = X.flatten()[:,None]
yyi = Y.flatten()[:,None]
uui = ui.flatten()[:,None]

x_initial = np.hstack([tti, xxi, yyi])
u_initial = uui

#plotting style-----------------------------------
fig = plt.figure(figsize = (8, 8))
ax = fig.add_subplot(111, projection="3d")
ax.plot_surface(X, Y, ui, cmap = "rainbow")
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("u")
plt.show()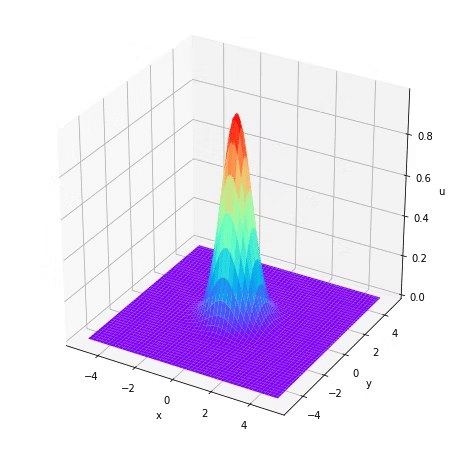

実装プログラム

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import scipy.io
from scipy.interpolate import griddata
from pyDOE import lhs
from mpl_toolkits.mplot3d import Axes3D
import time
import matplotlib.gridspec as gridspec
from mpl_toolkits.axes_grid1 import make_axes_locatable
import matplotlib.animation as animation

#ランダム生成値の固定---------------------------------
np.random.seed(1234)
tf.set_random_seed(1234)

class PhysicsInformedNN:

    #インスタンスが生成されたときに実行される関数
    def __init__(self, X_u, u, X_f, layers, lb, ub):
        self.lb = lb
        self.ub = ub
        self.t_u = X_u[:,0:1]
        self.x_u = X_u[:,1:2]
        self.y_u = X_u[:,2:3]
        self.t_f = X_f[:,0:1]
        self.x_f = X_f[:,1:2]
        self.y_f = X_f[:,2:3]
        self.u = u
        self.layers = layers
        self.weights, self.biases = self.initialize_NN(layers)
        self.sess = tf.Session(config=tf.ConfigProto(allow_soft_placement=True, log_device_placement=True))

        self.t_u_tf = tf.placeholder(tf.float32, shape=[None, self.t_u.shape[1]])
        self.x_u_tf = tf.placeholder(tf.float32, shape=[None, self.x_u.shape[1]])  
        self.y_u_tf = tf.placeholder(tf.float32, shape=[None, self.y_u.shape[1]])       
        self.u_tf = tf.placeholder(tf.float32, shape=[None, self.u.shape[1]])
        self.t_f_tf = tf.placeholder(tf.float32, shape=[None, self.t_f.shape[1]])
        self.x_f_tf = tf.placeholder(tf.float32, shape=[None, self.x_f.shape[1]])
        self.y_f_tf = tf.placeholder(tf.float32, shape=[None, self.y_f.shape[1]])
        self.u_pred = self.net_u(self.t_u_tf, self.x_u_tf, self.y_u_tf) 
        self.f_pred = self.net_f(self.t_f_tf, self.x_f_tf, self.y_f_tf)  

        self.loss = tf.reduce_mean(tf.square(self.u_tf - self.u_pred)) + \
                    tf.reduce_mean(tf.square(self.f_pred))    
        self.optimizer = tf.contrib.opt.ScipyOptimizerInterface(self.loss, method = 'L-BFGS-B', 
                                                                options = {'maxiter': 50000,
                                                                           'maxfun': 50000,
                                                                           'maxcor': 50,
                                                                           'maxls': 50,
                                                                           'ftol' : 1.0 * np.finfo(float).eps})
        init = tf.global_variables_initializer()
        self.sess.run(init)

    #初期のweightとbiasの生成
    def initialize_NN(self, layers):
        weights = []
        biases = []
        num_layers = len(layers)
        for l in range(0, num_layers-1):
            W = self.xavier_init(size=[layers[l], layers[l+1]])
            b = tf.Variable(tf.zeros([1,layers[l+1]], dtype=tf.float32), dtype=tf.float32)
            weights.append(W)
            biases.append(b)
        return weights, biases

    #切断正規分布に従うweightのランダム初期値を生成
    def xavier_init(self, size):
        in_dim = size[0]
        out_dim = size[1]
        xavier_stddev = np.sqrt(2/(in_dim + out_dim))
        return tf.Variable(tf.truncated_normal([in_dim, out_dim], stddev=xavier_stddev), dtype=tf.float32)

    #ニューラルネットワークの構築
    def neural_net(self, X, weights, biases):
        num_layers = len(weights) + 1
        H = 2.0*(X - self.lb)/(self.ub - self.lb) - 1.0
        for l in range(0, num_layers-2):
            W = weights[l]
            b = biases[l]
            H = tf.tanh(tf.add(tf.matmul(H, W), b))
        W = weights[-1]
        b = biases[-1]
        return tf.add(tf.matmul(H, W), b)

    #出力uのニューラルネットワーク
    def net_u(self, t, x, y):
        return self.neural_net(tf.concat([t,x, y],1), self.weights, self.biases)

    #出力fのニューラルネットワーク(自動微分)
    def net_f(self, t, x, y):
        u = self.net_u(t, x, y)
        u_t = tf.gradients(u, t)[0]
        u_x = tf.gradients(u, x)[0]
        u_xx = tf.gradients(u_x, x)[0]
        u_y = tf.gradients(u, y)[0]
        u_yy = tf.gradients(u_y, y)[0]
        #>>>>>>>>解きたい方式::::::::::::::::::::::::::::::::
        return u_t - u_xx - u_yy

    #コールバック関数の定義
    def callback(self, loss):
        print('Loss:', loss)

    #ニューラルネットワークのトレーニング
    def train(self):
        tf_dict = {self.x_u_tf: self.x_u,
                   self.t_u_tf: self.t_u,
                   self.y_u_tf: self.y_u,
                   self.u_tf: self.u,
                   self.x_f_tf: self.x_f,
                   self.t_f_tf: self.t_f,
                   self.y_f_tf: self.y_f}
        self.optimizer.minimize(self.sess, feed_dict = tf_dict,
                                fetches = [self.loss], loss_callback = self.callback)

    #出力されたuの格子点(X_star)の値を変数に代入
    def predict(self, X_star):
        return self.sess.run(self.u_pred, {self.t_u_tf: X_star[:,0:1], 
                                           self.x_u_tf: X_star[:,1:2], 
                                           self.y_u_tf: X_star[:,2:3]})

if __name__ == "__main__":

    #>>>>>>>設定--------------------------------------------------
    N_u = 1000   #初期条件と境界条件の学習データ数
    N_f = 30000  #コロケーションポイントの数
    x0 = -5      #xの始点
    x1 = 5       #xの終点
    y0 = -5      #yの始点
    y1 = 5       #yの終点
    t0 = 0       #tの始点
    t1 = 1       #tの終点
    layers = [3, 20, 20, 20, 20, 20, 20, 20, 20, 1] #NNの構造
    N = 200      #x,yの分割数
    Nt = 100     #tの分割数
    #>>>>>>>設定--------------------------------------------------

    #初期条件------------------------------------------------------
    xi = np.linspace(x0, x1, N)
    yi = np.linspace(y0, y1, N)
    Xi, Yi = np.meshgrid(xi, yi)
    ui = np.exp(-(Xi**2 + Yi**2))

    tti = np.zeros(N*N)[:,None]
    xxi = Xi.flatten()[:,None]
    yyi = Yi.flatten()[:,None]
    uui = ui.flatten()[:,None]

    X_u_train = np.hstack([tti, xxi, yyi])
    u_train = uui

    #初期条件データをNuの数だけ抽出する----------------------------------
    idx = np.random.choice(X_u_train.shape[0], N_u, replace=False)
    X_u_train = X_u_train[idx, :]
    u_train = u_train[idx,:]

    #三次元座標格子点の生成---------------------------------------------
    x = np.linspace(x0, x1, N)
    y = np.linspace(y0, y1, N)
    t = np.linspace(t0, t1, Nt)
    X, Y, T = np.meshgrid(x, y, t)

    tt = T.flatten()[:,None]
    xx = X.flatten()[:,None]
    yy = Y.flatten()[:,None]
    X_star = np.hstack([tt, xx, yy])

    #コロケーションポイントの生成----------------------------------------
    lb = np.array([t0, x0, y0])  #<lower bound>
    ub = np.array([t1, x1, y1])  #<upper bound>
    X_f_train = lb + (ub-lb)*lhs(3, N_f)
    X_f_train = np.vstack((X_f_train, X_u_train))

    #PhysicsInformedNNクラスにデータを渡す------------------------------
    model = PhysicsInformedNN(X_u_train, u_train, X_f_train, layers, lb, ub)

    #演算の実行-------------------------------------------------------
    start_time = time.time()
    model.train()
    run_time = time.time() - start_time
    print('Training time:', run_time)

    #演算結果を変数に格納--------------------------------------------
    u_pred = model.predict(X_star)

    #Plotting style-----------------------------------------------
    ims = []    #gifアニメーションの格納箱
    fig = plt.figure()
    for j in range(Nt):
        U = []
        for i in range(N*N):
            U = np.append(U, u_pred[Nt*i + j])
        U = U.reshape(N, N)
        im = plt.imshow(U,interpolation='nearest', extent=[x0, x1, y0, y1],
                        cmap='rainbow', vmin=0, vmax=1)
        ims.append([im])
    ani = animation.ArtistAnimation(fig, ims, interval=50)
    plt.colorbar()
    ani.save("output.gif", writer="imagemagick")
    plt.show()

実行結果

以下のようなgifアニメーションが作成されました。

3次元で拡張しても簡単な微分方程式であれば高い精度で数値計算ができます。学習時間は2次元の時と比べて10倍ほどかかりました。