変数の組$${\vec{w}}$$の関数を$${f(\vec{w})}$$書きます。ここで変数の組$${\vec{w}}$$を具体的に書くと、$${\vec{w} = (w_{1},w_{2},…)}$$となっていて、今は変数の個数は指定しないことにします。さて今、関数$${f(\vec{w})}$$の極値を求める問題を以下の制約条件の下で解きたいとします。

$$
g_{i} (\vec{w}) \geq 0 　　\text{for all}\,\,i.
$$

このとき次の双対な極値問題の解が、上の問題の解と一致することが知られています。

[Lagrange 双対問題]
$${\mathcal{L}(\vec{w}, \lambda): = f(\vec{w}) - \sum_{i} \lambda_{i} g_{i}(\vec{w})}$$
で定義される関数$${\mathcal{L}(\vec{w}, \lambda)}$$の$${\vec{w}}$$に関する極小化、$${\lambda}$$に関する極大化問題。
ここで極値$${\vec{w}^{\ast}}$$,$${\lambda^{\ast}_{i}}$$は以下のKKT(Karush-Kuhn-Tucker)条件を満たすように選ぶ必要があります。

1. $${\nabla_{w} \mathcal{L} |_{\vec{w}^{\ast}, \lambda^{\ast}_{i}} =0}$$

2. $${\lambda_{i}^{\ast} \geq 0}$$

3. $${g_{i}(\vec{w}^{\ast}) \geq 0}$$

4. $${ \sum_{i} \lambda^{\ast}_{i} g_{i}( \vec{w}^{\ast}) = 0 }$$ 

というわけなのですが、どうして$${min_{\vec{w}} \, max_{\lambda}\, \mathcal{L}(\vec{w}, \lambda)}$$の解が元の制約付き極値問題の解に一致したりするのでしょう? 
前置きが長くなりましたが、本記事ではこのことの(テキトーな)説明を試みたいです。

視覚的に理解するために2変数かつ制約条件が一つの場合を考えます。すなわち$${\vec{w} = (w_{1},w_{2})}$$であり、制約条件は

$$
g(w_{1},w_{2} ) \geq 0
$$

のみです。
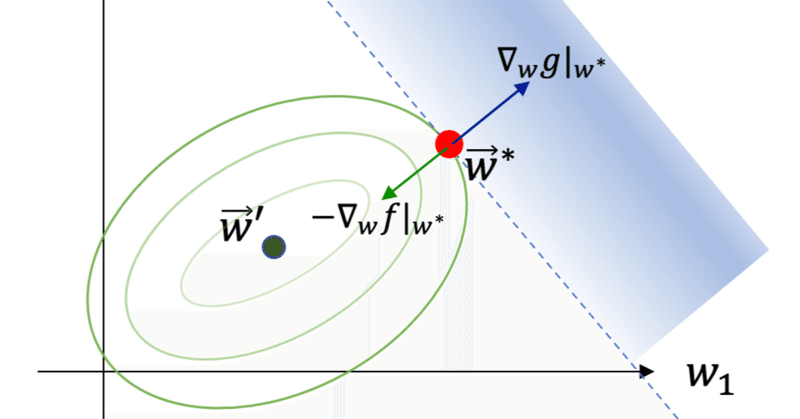
仮に制約条件がなかったとした場合の関数$${f(\vec{w})}$$の極小点を以下$${\vec{w}'}$$と書きます(以下大域的極小点とも呼ぶ)。このとき、関数$${f(\vec{w})}$$の制約付き極値問題の解$${\vec{w}^{\ast}}$$が定まる様子は下の図のように理解できます。
大域的極小点$${\vec{w}'}$$を囲う薄緑の線は$${f(\vec{w})}$$の等高線です(濃くなるほど値が大きい)。$${\vec{w}'}$$から出発して$${f(\vec{w})}$$が大きくなる方向に進むとき、初めて制約条件を満たす点が解$${\vec{w}^{\ast}}$$(赤い点)となります。

制約付き極小問題の解$${\vec{w}^{\ast}}$$において、二つのベクトルを考えてみましょう。まず$${ \nabla_{w} g|_{w^{\ast}} }$$ですが、このグラディエントのうち制約境界方向の成分は0になる(制約境界上では$${g=一定=0}$$)ため、制約境界に直交する成分しか持ちません。したがって、$${ \nabla_{w} g|_{w^{\ast}} }$$は上図のように制約境界に直交します。
一方、ベクトル$${- \nabla_{w} f|_{w^{\ast}} }$$の等高線に沿った成分は0になるため、$${- \nabla_{w} f|_{w^{\ast}} }$$は等高線に垂直な成分しか持ちません。したがってこちらも制約境界に直交する方向を向きます。
以上のようなわけで二つのベクトル$${ \nabla_{w} g|_{w^{\ast}} , \, \,- \nabla_{w} f|_{w^{\ast}} }$$は並行であり方向が逆になっています。
よって、正の定数$${\lambda^{\ast}>0}$$が存在して$${\vec{w}^{\ast}}$$では次が成立します。

$$
- \nabla_{w} f + \lambda^{\ast} \nabla_{w} g =0  \,\,\,\,\text{at}\,\, \vec{w} = \vec{w}^{\ast}
$$

書き換えると、

$$
\nabla_{w } (f - \lambda^{\ast} g) = 0   \,\,\,\,\text{at}\,\, \vec{w} = \vec{w}^{\ast}　　　
$$

したがって、求めたい制約付き極小点では特別な正の定数$${\lambda^{\ast}}$$を用いて関数$${f- \lambda^{\ast} g}$$が$${\vec{w}}$$について極小化されていることになります。これが双対問題において$${f- \lambda g}$$を考える理由です。
次に$${\lambda}$$の値がどう決まるのか議論しましょう。
$${\vec{w} = \vec{w}^{\ast}}$$で成り立つ式$${\nabla_{w } (f - \lambda^{\ast} g) = 0}$$に戻ります。このときグラディエントは制約境界に垂直な成分しか持たないので、制約境界の法ベクトル方向のパラメータを$${s}$$として以下の形に書き直せます。

$$
\frac{d}{ds} (f - \lambda^{\ast} g)=0 \,
\to \, \lambda^{\ast} = \frac{df/ds}{dg/ds}|_{\vec{w} = \vec{w}^{\ast} } 
\, \to \,  \lambda^{\ast} = \frac{df}{dg}|_{\vec{w} = \vec{w}^{\ast} }
$$

これが、「うまいパラメータ」$${\lambda^{ \ast}}$$を与える式です。
実はこの式で与えられる$${\lambda^{\ast}}$$は、$${\mathcal{L} := f- \lambda g}$$の$${\vec{w} =  \vec{w}^{\ast}}$$における停留点になっています。
チェックしてみましょう。

$$
\frac{d \mathcal{L}}{d \lambda} |_{\vec{w}^{\ast}, \lambda^{\ast}} =
 \frac{df}{d\lambda}|_{\vec{w}^{\ast}, \lambda^{\ast}}- g(\vec{w}^{\ast}) - \lambda^{\ast} \frac{dg}{d\lambda}|_{\vec{w}^{\ast}, \lambda^{\ast}}
$$

ここで右辺2項目は$${\vec{w}^{ \ast}}$$が制約境界上にあるため０になります。
したがって、

$$
\begin{array}{}
\frac{d \mathcal{L}}{d \lambda} |_{\vec{w}^{\ast}, \lambda^{\ast}} &=&
 \frac{df}{d\lambda}|_{\vec{w}^{\ast}, \lambda^{\ast}}- \lambda^{\ast} \frac{dg}{d\lambda}|_{\vec{w}^{\ast}, \lambda^{\ast}}  \\
&=& \left( \frac{df}{d \lambda} - \frac{df}{dg}\frac{dg}{d \lambda}  \right)|_{\vec{w}^{\ast}, \lambda^{\ast}} \\
&=& 0
\end{array}
$$

したがって、我々は元の制約付き極値問題を解く代わりに、関数$${\mathcal{L}:=f- \lambda g}$$を定義して$${min_{\vec{w}} \, max_{\lambda}\, \mathcal{L}(\vec{w}, \lambda)}$$を解いたら良いわけです。
最後に解を選択する際の基準になるKKT条件の意味についてコメントしておきます。条件1,2を課すべきことは上の説明から明らかです。条件3は元の問題の制約条件を解$${\vec{w}^{\ast}}$$が満たすべきだという当たり前の式です。条件4は$${\mathcal{L}}$$の極値が元の問題の極値$${f(\vec{w}^{ \ast})}$$に等しくなることを保証するための条件です。

参考文献
"ゼロから作るPython機械学習プログラミング　入門", 八谷大岳,