フーリエ変換、短時間フーリエ変換

2024年4月7日 17:16

導入

フーリエ変換とその周辺の理解を深めるためにRでシミュレーションをおこなった。まず$${f(x)}$$という関数のフーリエ級数展開を数式で書くと、

$${f(x) = \frac{a_0}{2} + \sum_{k=1}^\infty (a_k cos(k \theta x) + b_k cos(k \theta x)) (k\in\mathbb{N}, \theta\in\mathbb{R}^{+})}$$

となる。これは関数を離散的に周波数成分に分けて足し合わせていると解釈できる。さらに複素数を用いることで、ある周波数（ある$${k}$$に対応する部分）の係数$${a_k}$$と$${b_k}$$を一つの$${c_k}$$にまとめて以下のように記述することができる。

$${f(x) =　\sum_{k=-\infty}^\infty c_k e^{i k \theta} (k\in\mathbb{N}, \theta\in\mathbb{R}^{+})}$$

フーリエ変換は周波数成分を（離散的にではなく）連続的にとらえたものであり、フーリエ級数展開における$${c_k}$$を求めることに相当する。$${f(x) =}$$という形での表現に対応するものはフーリエ逆変換と呼ばれる。
フーリエ変換を数式で表す場合、周波数に対応する変数を$${(\theta}$$の自然数倍である$${k \theta }$$として離散的に表現するのではなく）単に$${\alpha}$$とおいて連続的に考えることとする。

$${\alpha}$$に対応するフーリエ変換は以下のように記述できる。

$${F(\alpha) = \int_{-\infty}^{\infty} f(x) e^{-i \alpha x} dx, (\alpha\in\mathbb{R})}$$

医学分野ではMRIなどの画像検査や脳波の解析で用いられている。分野的には脳神経領域と親和性が高いように思う。

Rでフーリエ変換

まず$${y=f(x)}$$を準備する。

dx=0.01
x <- seq(-10, 10, by=dx)


mask1 <- rep(0, length(x))
mask2 <- rep(0, length(x))
mask1[(2/dx):(9/dx)] <- 1 
mask2[(15/dx):(19/dx)] <- 1 

# 正弦曲線、余弦曲線を適当に伸縮、シフトさせて切り取って足し合わせたものをつくる
y1 <- sin(3*(x-0.2)) * mask1
y2 <- cos(2*(x-0.4)) * mask1
y3 <- sin(10*(x-0.6)) * mask2
y4 <- cos(9*(x-0.8)) * mask2
eps <- rnorm(length(x))*0.1
y <- y1 + y2 + y3 + y4 + eps 
plot(x, y, xlim=c(-10, 10), type = "l")

次にフーリエ変換を実行する。

# フーリエ変換
alpha <- seq(0, 10, by=0.01)
power <- - matrix(complex(real=0,imaginary=1) * alpha, ncol=1) %*% matrix(x, nrow=1)
tile_fx <- matrix(rep(y, dim(power)[1]), nrow=dim(power)[1], byrow=T)
tmp_mat <- exp(power) * tile_fx * dx

Fourier <- apply(tmp_mat, 1, sum)
spectrum <- sqrt(Re(Fourier)^2+Im(Fourier)^2)
plot(alpha, spectrum, xlim=c(0, 10), type = "l", xaxp=c(0, 10, 10))

すると、以下のような結果になる。

$${y_1,y_2, y_3, y_4}$$と対応して予想通り$${\alpha=2,3,9,10}$$のところにピークがくる。しかしフーリエ変換では無限に広がる正弦関数、余弦関数を用いているため周波数成分ごとに分割することはできても、その位置（$${x}$$軸のどのあたりに波があるか）についての情報は得られない。

その点を克服するよう工夫したものとして、短時間フーリエ変換（short-time Fourier transform: STFT）がある。

短時間フーリエ変換（short-time Fourier transform: STFT）

$${f(x)}$$をSTFTする場合、おおざっぱな説明ではあるが、ある範囲の$${x}$$を除きあとは0になるような窓関数を作成し、$${f(x)}$$にそれをかけて$${f(x)}$$を切り取ったものを作りそれをフーリエ変換する、ということを窓を動かしながら繰り返すことで、どの場所（どの$${x}$$あたり）にどんな周波数の波があるかを見出すというアイデアである。

数式で書くと以下のようになる。

$${STFT(x, \alpha) = \int_{-\infty}^{\infty} f(z) w(z-x) e^{-i \alpha z} dz, (\alpha\in\mathbb{R})}$$

となる。
Rでシミュレーションする。ここでは$${w(x) = \begin{cases} 1&(x\in{[-c, c]}) \\ 0 &(else)\end{cases} }$$を用いる。

# 短時間フーリエ変換
# [t-c, t+c]で１、他は0であるような関数を窓として実行してみる
tile_zero <- matrix(0, nrow = dim(tmp_mat)[1], ncol = dim(tmp_mat)[2])
ans <- matrix(0, nrow = dim(tmp_mat)[1], ncol = dim(tmp_mat)[2])

# ここでは工夫せず愚直に計算する
cs <- c(0.3, 1, 3)

start = proc.time()
for (c in cs){
  for (i in 1:length(x)){
  
    tmp_left <- max(i - c/dx, 1)
    tmp_right <- min(i + c/dx, length(x)) 
    window <- tile_zero
    window[,tmp_left:tmp_right]<-1
    
    tmp_mat_short <- tmp_mat * window
    
    Fourier_short <- apply(tmp_mat_short, 1, sum)
    spectrum_short <- sqrt(Re(Fourier_short)^2+Im(Fourier_short)^2)
    ans[, i] <- spectrum_short
    
  }
  
  
  # 横軸に位置、縦軸に周波数（と対応するもの）の値をとって可視化する
  image(x, alpha, t(ans), main=stringr::str_glue("c={c}"))

}
print(proc.time()-start) # 処理時間を計測しておく

不確定性原理により、周波数と位置の両方の情報を精度よく得ることはできないことが証明されている。実際に以下の画像のように$${c}$$を小さくすると位置に関する解像度はよくなるが周波数に関する解像度は小さくなり、$${c}$$を大きくするとその逆の現象が観察される。

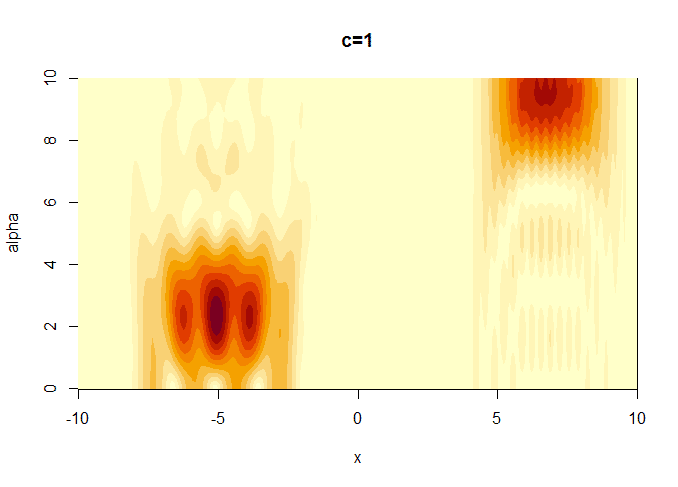
ここでは、cは$${f(x)}$$wを切り取る窓の幅を規定するので、狭い範囲での切り取り（小さい$${c}$$に対応）波の切り抜きから周波数を判定するのは困難になる一方、波に（相対的に）接近しないと切り取ることができない分位置は正確に把握できるし、大きい$${c}$$の場合はその逆のことが起こるのは直観的にも理解できる。

フーリエ変換、短時間フーリエ変換

導入

Rでフーリエ変換

短時間フーリエ変換（short-time Fourier transform: STFT）

関連する話題