量子論について理解するためには，線形代数に関する知識が少なからず必要になるはずです。その理由は，量子論では線形写像を考えることが実質的に不可欠であるためといえるでしょう。そもそも，なぜ量子論では線形写像が現れるのでしょうか？その理由を，量子論の専門家ではない人にできるだけわかりやすく説明します。

量子論では，大別すると2種類の線形写像が現れます。これらを区別できれば，量子論に関する理解が大幅に深まることと思います。

準備：線形写像とは

まず，線形写像についてざっくりと説明しておきます。ある集合$${X}$$からある集合$${Y}$$への写像$${f}$$が線形であるとは，任意の$${x_1,\dots,x_k \in X}$$と$${a_1,\dots,a_k \in \R}$$（$${\R}$$は実数全体）に対して

$$
f \left( \sum_{i=1}^k a_i x_i \right) = \sum_{i=1}^k a_i f(x_i) \qquad(1)
$$

を満たすことを意味します（図式と数式の両方を示しています）。この式は，次のように解釈することができます。

図式：両辺にある丸括弧を消しても意味が変わらない。
数式：左辺の$${f(\dots)}$$の括弧の中にある和と実数倍という演算を右辺のように括弧の外に出しても値が変わらない。

もう少し補足をすると，上記では実ベクトル空間に対する線形写像を説明しています。$${X}$$と$${Y}$$は和と実数倍という二つの演算が適切に定まっているような集合（つまり実ベクトル空間）であることを暗に仮定しています。複素ベクトル空間について考えたい場合は，上記の$${\R}$$を$${\Complex}$$（複素数全体）に置き換えるだけです。

確率的なふるまいにより現れる線形代数（実ベクトル空間）

まず，一つ目の線形写像について説明します。

物理学では，『状態』と『測定』という概念がよく用いられます。大ざっぱに説明すると，ある物体の『状態』とは，その物体にいろいろな操作を施したときのふるまいを定めるための概念であるといえます。また，『測定』とはいくつかの値の候補（たとえば$${\{1,2,\dots,6\}}$$）の中から一つ（たとえば2）を返すような操作のことだといえます。返された値は，測定結果とよばれます。以下では，『状態』と『測定』が満たすべき条件について考えることにします。

話を単純化するため，以降では測定結果の候補を$${\{1,\dots,M\}}$$とします（測定結果が連続値である場合などに拡張することは容易です）。状態を$${\rho}$$のように表し，測定を$${\Pi}$$のように表すことにします。量子論では測定を行ったときの確率が重要になります。状態が$${\rho}$$であるような物体に対して測定$${\Pi}$$を行ったときに測定結果$${m \in \{0,\dots,M\}}$$が得られる確率を，$${\Pi_m(\rho)}$$と書くことにします。例を挙げておきます。

1. 測定結果として必ず$${n}$$を返すような測定を行った場合：$${\Pi_n(\rho)=1}$$および$${\Pi_m(\rho)=0 ~(\forall m \neq n)}$$が成り立ちます。

2. 状態$${\rho}$$に含まれている情報を完全に無視してランダムに値を返すような測定を行った場合：$${\rho}$$とは無関係に常に$${\Pi_m(\rho)=1/M}$$が成り立ちます。

状態$${\rho}$$と測定$${\Pi}$$をどのように選んでも，個々の測定結果が得られる確率は0以上であり，（測定器が壊れたりしない限り）必ず何らかの測定結果が得られる必要があります。このことから，次式を満たす必要があることがわかります。

$$
\Pi_m(\rho) \ge 0, \quad\sum_{m=1}^M \Pi_m(\rho) = 1 \qquad(2)
$$

なお，この式から$${\Pi_m(\rho) \le 1}$$という条件も得られます。状態$${\rho}$$に対して測定$${\Pi}$$を行ったときの測定結果の確率分布は，組$${\{\Pi_1(\rho),\dots,\Pi_M(\rho)\}}$$で表せます。

また，ある確率分布 $${\{p_1,\dots,p_k\}}$$に対して，「状態$${\rho_1,\dots,\rho_k}$$のいずれかをランダムにとり，状態$${\rho_i}$$である確率が$${p_i}$$である」という状態$${\sigma}$$を考え，この状態を形式的に

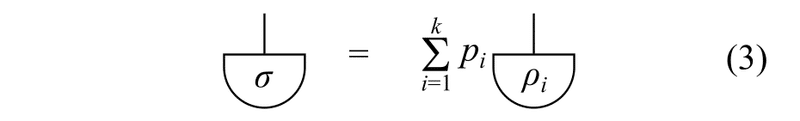
$$
\sigma = \sum_{i=1}^k p_i \rho_i \qquad(3)
$$

と書くことにします。このとき，確率$${\Pi_m(\sigma)}$$は次式を満たすべきでしょう。

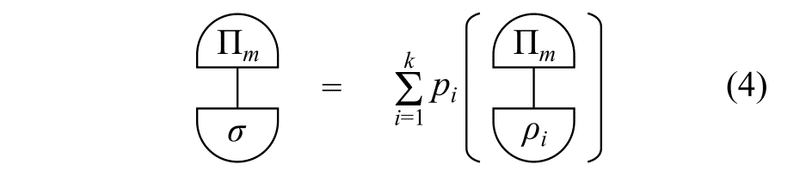
$$
\Pi_m(\sigma) = \sum_{i=1}^k p_i \Pi_m(\rho_i) \qquad(4)
$$

式(4)に式(3)を代入すると

$$
\Pi_m \left( \sum_{i=1}^k p_i \rho_i \right) = \sum_{i=1}^k p_i \Pi_m(\rho_i) \qquad(5)
$$

が得られます。ここで，$${p_i}$$や$${\Pi_m(\rho_i)}$$は確率ですので0以上1以下の値をとるのですが，いったんこの制約を外して任意の実数をとり得ると仮定します。つまり，$${\Pi_m(\rho_i)}$$については式(2)で示した制約を考えないことにします（$${p_i}$$についても同様）。このように制約を外して議論を進めてから，最後に0以上1以下であるという制約を設けても結果は変わりません。また，いったん制約を外して考えたほうがしばしば見通しがよくなります。

すると，式(5)を満たすことは$${\Pi_m}$$が線形写像であることに等しいことがわかります（実際，式(1)に$${f = \Pi_m}$$を代入した式と同じ形をしています）。このようにして，確率分布がもつ基本的な性質を考えれば線形写像がほぼ必然的に現れます。線形代数では，和とスカラー倍（ここでは実数倍）という二つの基本的な演算が登場しますが，和が確率の和に相当し，実数倍が結合確率に相当することになります。

上記の議論では，量子論ではなく古典論に対してもそのまま当てはまります。それどころか，『状態』に対して『測定』を行ったときの確率について考えたい場合には，量子論や古典論に限らず汎用的に当てはまります。このような考え方に基づいて，測定（やその他の各種操作）を行ったときの確率的なふるまいを調べるという理論は，操作的確率論または一般確率論とよばれています。

以降では，量子論に特化した話をしておきます。（有限次元系の）量子論では，状態はトレースが1であるような複素半正定値行列（密度行列とよばれます）で表されます。量子論では密度行列の和や実数倍という演算がよく行われますが，これらの演算が上記で説明した和と実数倍にそのまま対応しています。また，線形写像$${\Pi_m}$$は，状態（つまり密度行列）$${\rho}$$に対して

$$
\Pi_m(\rho) = \mathrm{Tr}(P_m\rho)
$$

を満たすような正方行列$${P_m}$$で表されます。$${\{\Pi_1(\rho),\dots,\Pi_M(\rho)\}}$$が$${\rho}$$によらず確率分布になる必要がありますが，この条件を満たすような行列の組$${\{P_1,\dots,P_M\}}$$はPOVM（Positive Operator-Valued Measure）とよばれます。測定を写像の組$${\{\Pi_1,\dots,\Pi_M\}}$$で表してもPOVM$${\{P_1,\dots,P_M\}}$$で表しても本質的な違いはありません。

対称性と局所性により現れる線形代数（複素ヒルベルト空間）

量子論で現れるもう一つの線形写像は，複素ヒルベルト空間に対するものです。具体的には，すでに述べた密度行列（とPOVM）がこの種の線形写像に該当します。こちらの線形写像については，上記の議論とは対照的に，操作的・確率的なふるまいのみからその必然性を導くことは非常に困難です。もしこれを容易に導出できる方法が見つかれば，量子論の分野において画期的な成果といえるようですので，現在も継続的に研究が行われています。誤解を恐れずにいえば，密度行列を素直には導出できないことが，量子論が我々の直感に反するような性質をもっていることと密接に関連しているといえるかもしれません。

ただし，いくつかの仮定さえ認めれば，その必然性を導くことはできます。以下では，その中の一つのアプローチについて，概要を説明します。

系$${A}$$の状態全体から成る集合を状態空間とよび，$${\mathrm{St}_A}$$とおきます。話を簡単にするため，各系は有限次元系（つまり，各状態空間を含む最小の実ベクトル空間が有限次元）であるとします。また，確率的・操作的な性質について考えた場合に最低限満たしていると思われるようないくつかの条件を満たすと仮定します（詳細は割愛します）。さらに，任意の系$${A,B}$$について次の二つの条件を満たすと仮定します。

1. 状態空間$${\mathrm{St}_A}$$があるきれいな対称性をもっている。具体的には，$${\mathrm{St}_A}$$を含む最小の凸錐が対称錐とよばれる集合になる（エフェクト空間とよばれる測定を表す空間についても同様）。

2. 系$${A}$$から系$${B}$$へのすべての操作$${f}$$が局所等価性とよばれる性質をもっている。局所等価性について大ざっぱに説明すると，入力系$${A}$$と出力系$${B}$$のみについて考えるだけで$${f}$$のふるまいを完全に特定できる（$${A,B}$$以外の系については考える必要がない）という性質のことです。

このとき，各系$${A}$$の状態が（$${A}$$毎に定まるあるサイズ$${N_A}$$の）密度行列と一対一に対応することを導けます。このようにして密度行列（つまり複素行列）が現れるため，複素ヒルベルト空間を考える必要が出てくるというわけです。とくに状態が純粋状態とよばれる特別な場合には，密度行列は列ベクトルで表すこともできます。この列ベクトルは波動関数とよばれます。

これらの条件や導出方法の詳細については，拙著『図式と操作的確率論による量子論』でしっかりと説明しています。また，状態が密度行列と一対一に対応することを導ければ（またはこのことを認めれば），測定がPOVMで表されることや，ほかの量子論に関する基本的な性質（例：ボルンの確率規則）が容易に得られます。これらについても本書（＆補足資料）で触れています。ご興味のある方はお読みくだされば幸いです。