Introduction：計量経済学への挑戦🔥

経済学部に通う私も
いよいよ大学「学部」最終年になり
学問に全力を注ぐ時間も限られてきました👍

「知は力なり」という言葉を信じて
残りの大学生生活を満喫したいと思います

学部レベルのマクロ経済学は
個人的によく理解できたつもりです

しかしながら、本当の経済の動向を理解するには、学部レベルの知識ではお話になりません😥
また、正しい計量経済学の知識やデータ分析のリテラシーを会得しなければなりません💦
現実の経済データを、理論モデルと当てはめ
正しい計量手法によって実証分析できる力を醸成したら
きっと将来どこかで活躍できる人財になれる可能性を高めることに繋がると思います

実際の経済動向や政治と結びつけながら
応用できる能力がなければ
知識を持つ意義も小さくなってしまいます💦

何事もアウトプット前提のインプットが
大事であると、noteで毎日発信してきました

これは、どのような内容で
あっても当てはまります👍

先行研究の論文を一概に読んでも
記憶に残っていなかったり
大切な観点を忘れてしまっていたりしたら
学習の進捗は滞ってしまうと思います

だからこそ、この「note」をフル活用して
自分の知識を1％でも、定着させ
誰にでもわかりやすい解説をアウトプットできるように努めていきたいと思います

私がこれからアウトプットする
計量経済学において最重要なパートである
時系列分析のモデル理論解説を
どうぞ最後まで、ご愛読ください📖

本投稿作成における参考文献は以下の通りです

なぜ、計量経済学を学ぶのか？？

計量経済学が時系列解析法を「理論なき計測」として退けるところからスタートしたことでよく知られているのです

1930年に創立された計量経済学会の規約第1条では、計量経済学は「理論的数量的アプローチと経験数量的アプローチの統一」と定義されていました📝
また、R・フリッシュによる『エコノメトリカ』創刊の辞では、「統計学、経済学、数学の三者の統合」と定義されているのです👍

このような定義においては、当時のハーバード景気予測に代表される時系列解析法への批判が強く意識されていたとされています

すなわち、それが29年の大恐慌の予測に失敗したのは，経済理論を無視し、 時系列データの形式的な解析のみに終始したからであったということです

今後はそうした「理論なき計測」の立場を退け、「理論に基づく計測」を重視していかなければならない、という見解の重要性が増しています
このような歴史を経て、計量経済学はスタートをきったのでした


そして、何よりマクロ経済変数は
その多くが互いに影響を及ぼし合う相互依存の関係にあり、また過去の変化の影響が持続するという傾向を持ちます

これらの動向を分析したり、将来を予測したりできるようになるためには、計量経済学、ひいては「時系列分析」に対する理論や正しい実証手法への理解が必要不可欠となります

「計量経済学」シリーズの投稿では、こうしたマクロ時系列変数の実証分析に必要な計量理論と手法を習得することを目的とします

これから私がアウトプットする
時系列マクロ経済分析に関する内容について
どうぞ最後までご愛読くださいね💖

前回のお復習い✨

非定常過程における時系列計量分析💛

今回は、非定常過程における時系列分析モデルを考えていくことにします

具体的には、単位根の検定、ADF検定の方法などを解説します
なお、参考文献は、以下の通りです✨

Dickey-Fuller 検定の概要🌟

以下では、前回の単位根検定に引き続き、Dickey-Fuller 検定を解説したいと思います

いま、ｙt がAR(1)過程に従っているとします

$$
y_t = \phi y_{y-1} +u_t \cdot\cdot\cdot①\\      \\u_t ～i.i.d(0,\sigma^2):White  Noise\\         \\        \\if, |\phi|< 1 \to y_t \equiv I(0)\\    \\if, |\phi|=1 \\\to y_t  has  "unit  root"  \equiv I(1)
$$

ただし、ｕt は期待値は 0 で一定の分散(σ^2)を持つホワイトノイズとします

もし|Φ|<1であればｙtはＩ(0)変数ですが
Φ＝1であれば、非定常過程になりますので「単位根」を持ち、Ｉ(1)変数となります

したがって、少し直観的に説明いたしますと
ｙt が定常かどうかを調べるためには
①式に最小自乗法(OLS)を適用して、以下のような仮説検定を行えば良いと思われます

$$
Hypothesis   Testing\\
H_0: \phi=1,  H_1:\phi< 1
$$

しかし、通常のｔ検定によりこの仮説検定を
行うと、ｔ統計量の分布は大きな歪みをもち、検定統計量として不適切なものになってしまうことが知られています🥲

そこで、これに代替する方法として
DickeyとFullerは、次のような検定方法を提案したのです

まず、1次の自己回帰AR(1)過程の式を
次のように変形します

そして、上記で述べた同様の検定を実施します

$$
\Delta y_t = \beta y_{t-1}+ u_t \cdot\cdot\cdot ②\\        \\where, \beta=\phi -1 \\     \\Hypothesis   Testing\\
H_0: \beta=1,  H_1:\beta< 1
$$

この検定は、①式における
Ｈ0：Φ＝1、Ｈ1：Φ< 1と同じになります

ただ、帰無仮説のもとで
推計されたβ^のｔ値は、ｔ分布に従わず
マイナス方向に寄った分布となります📝

よって、通常のｔ検定は、帰無仮説を過剰に
棄却する可能性が高いということです

つまり、通常のｔ検定では
本来1次の和分過程Ｉ(1)変数であるものを誤って、0次の和分過程Ｉ(0)変数であると判断する可能性が高くなってしまいます💦

そこで、Dickey と Fuller は
単位根の検定を行うために、次の3つの回帰式を設定し、各回帰式の β の推定量に対する分布表を提示しました

これは、Dickey-Fuller分布（DF分布）として知られており、このような検定はDickey-Fuller検定（DF検定）と呼ばれています

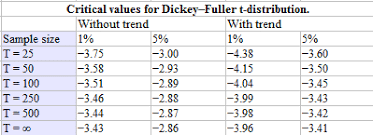
$$
Dickey-Fuller  test\\      \\\Delta y_t =\beta y_{t-1}+u_t \cdot\cdot\cdot ③\\     \\\Delta y_t =μ+\beta y_{t-1}+u_t\cdot\cdot\cdot ④\\    \\\Delta y_t =μ+\delta t +\beta y_{t-1}+u_t\cdot\cdot\cdot ⑤
$$

上記で定式化したいずれのモデルにおいても、β＝0であれば、ｙtは単位根を持ちます

なお、これら3つの基本的な相違点は、回帰式における確定項(deterministic  term)の定式化の相違です

③式には、確定項はありません
しかし、④式には、確定項として定数項が含まれています

そして、⑤式には、定数項とタイムトレンドが含まれていることを今一度確認しておくことにしましょう

なお、ＤＦ検定において、③式、④式、および⑤式の誤差項 utは、ホワイトノイズであることが仮定されています

Augumented Dickey-Fuller 検定

しかし、場合によっては、誤差項に系列相関が存在する可能性があります

そのような場合には、非説明変数の過去の値を含む形の回帰式を考えて、単位根の検定が行われます

$$
Unit  Root  testing\\   \\
\Delta y_t =\beta y_{t-1}+\displaystyle\sum_{i=1}^n\gamma_i\Delta y_{t-i}+u_t \cdot\cdot\cdot ③'\\    \\\Delta y_t =μ+\beta y_{t-1}+\displaystyle\sum_{i=1}^n\gamma_i\Delta y_{t-i}+u_t\cdot\cdot\cdot ④'\\      \\
\Delta y_t =μ+\delta t +\beta y_{t-1}+\displaystyle\sum_{i=1}^n\gamma_i\Delta y_{t-i}+u_t\cdot\cdot\cdot ⑤'
$$

このように、右辺に
被説明変数の過去の値を含めて行う単位根検定は、augumented Dickey-Fuller 検定（ADF検定）と呼ばれます

つまり、ＤＦ検定は、ＡＤＦ検定において
拡張項の次数が、0の場合の特殊ケースということが判明します

ここで注意すべきポイントは以下の通りです⚠️

通常のｔ検定であれば、ｔ分布表は回帰式の
決定項の定式化には依存していません

しかし、これに対して、単位根の検定においては、決定項の定式化の相違によって、用いる分布表が異なっているという点です

したがって、回帰分析によって得られたｔ値を適切な表を用いて分析する必要があるということです

何よりポイントとして、単位根検定においては、ｔ統計量はｔ分布に従わず、Dickey-Fuller分布に従うことになる点を抑えておきましょう🥰

$$
t - statistics  of  Unit  root  testing\\     \\t≦DF_{\alpha} \to H_0  Rejected \\t>DF_{\alpha} \to H_0  Accepted  \\
$$

ただし、DFαはDickey-Fuller分布の下側100α％点です

実証分析において、しばしば問題となるのは「いかにして適切な拡張項の次数を決めるか」という点です

含まれる拡張項の次数が大きすぎると検定の検出力が落ちます

逆に、含まれる拡張項の次数が少なすぎると、検定のサイズにゆがみが生じることになってしまいますので、正しい推計結果を得ることが困難になってしまうということです💦

したがって、何より構築したモデルが適切な次数で分析されることが大切であると言えます

ADF検定における最適な次数選択

ADF検定における拡張項の最適な次数選択において、通常、以下の5つの方法がよく用いられますので、ご紹介したいと思います

(1)拡張項を適当な次数（短めの次数）から開始して、その都度、誤差項の系列相関の検定を行います

もし、誤差項に系列相関があると判断されれば、系列相関がなくなるまで、拡張項の次数を増加させていくことになります

(2)拡張項を適当な次数（長めの次数）から始めて順番を減らし、拡張項の最大次数の回帰係数(γp)が統計的に有意となるところに次数を決定します

(3)拡張項の次数を、AICやSBIC等の情報量基準を用いて決めます

(4)先見的に選択されたいくつかの次数に基づいて、分析を行い（例えば、四半期データであれば、4期と8期など）その結果の頑健性を確認します

(5)Schwert(1989)は、ｐをＴの関数として、以下の条件を満たす整数部分として次数を定める方法を提示しました

$$
Schwert's  Method\\   \\
\\p=12(\frac{T}{100})^{1/4}
$$

当然ながら、これらの方法を組み合わせて使うことも有効と言えます

例えば、SBIC情報量基準で暫定的に次数を決定したのちに、それから、Ljung-Box検定などを用いて、誤差項の系列相関についてチェックすることも、実証分析を進める上で有力な方法と言えるのです👍

プラスワントピック：和記号の計算💎

以下では、計量経済学だけではなくあらゆる場面で登場することが多い和記号Σについて解説したいと思います

いま、x1,x2,･･･xn が与えられたとき、以下のように和記号を定義します

$$
Sum  symbol\\     \\
\textstyle\sum_{i=1}^nx_i =x_1+x_2 \cdot\cdot\cdot x_n
$$

和記号を用いた計算

{xi},{yi}が与えられたとき、和記号Σに関して、以下の性質が成り立つことを前回の投稿で確認しました

今回は、より和記号Σを有効に活用する計算方法をご紹介します
和記号Σを用いると、複雑な計算をより簡単に行うことができます

まずは、標本平均は以下のように表記できます
この計算プロセスを一度はしたことがあるのではないでしょうか？

$$
Sample  Mean:\bar x
\\    \\\bar x=\frac{1}{n}(x_1+x_2+\cdot\cdot\cdot +x_n)\\     \\     =\frac{1}{n}\displaystyle\sum_{i=1}^n x_i\\    \\     \\\Lrarr  \bar x\times n =\displaystyle\sum_{i=1}^n x_i
$$

続いて、平均からの偏差の和を求めてみましょう

$$
\displaystyle\sum_{i=1}^n (x_i-\bar x)\\=\displaystyle\sum_{i=1}^n x_i-\displaystyle\sum_{i=1}^n \bar x\\                      \\=\displaystyle\sum_{i=1}^n x_i -n \bar x =0
$$

先程の、標本平均の関係性を使えば、平均からの偏差の和は0になることがわかりました👍

また、標本平均からの偏差の自乗和は、以下のようになります

$$
\displaystyle\sum_{i=1}^n (x_i-\bar x)^2\\=\displaystyle\sum_{i=1}^n (x_i^2-2x_i\bar x+\bar x^2)\\   \\=\displaystyle\sum_{i=1}^n x_i^2 -2\bar x \displaystyle\sum_{i=1}^n x_i+n \bar x^2 \\     \\=\displaystyle\sum_{i=1}^n x_i^2 -2n\bar x^2 +n \bar x^2\\     \\=\displaystyle\sum_{i=1}^n x_i ^2 -n \bar x ^2 \\    \\(=\displaystyle\sum_{i=1}^n x_i^2 -\frac{1}{n}\displaystyle\sum_{i=1}^n x_i)^2
$$

本日の解説は、ここまでといたします📝
計量経済学：時系列分析は、卒業論文執筆において欠かせない知識です
また、このようなデータに対する分析力を身につけることは、自らの将来的な市場価値向上につながる可能性が高いと言えます

また、和記号の計算などは、受験勉強において必須の知識です
ぜひ、これらの投稿が何かお役立てになれば、幸いです💛

付録：私の卒論研究テーマについて🔖

私は「為替介入の実証分析」をテーマに
卒業論文を執筆しようと考えています📝

日本経済を考えたときに、為替レートによって
貿易取引や経常収支が変化したり
株や証券、債権といった金融資産の収益率が
変化したりと日本経済と為替レートとは
切っても切れない縁があるのです💝
（円💴だけに･･･）

経済ショックによって
為替レートが変化すると
その影響は私たちの生活に大きく影響します

だからこそ、為替レートの安定性を
担保するような為替介入はマクロ経済政策に
おいても非常に重要な意義を持っていると
推測しています

決して学部生が楽して執筆できる簡単なテーマを選択しているわけでは無いと信じています

ただ、この卒業論文をやり切ることが
私の学生生活の集大成となることは事実なので
最後までコツコツと取り組んで参ります🔥

本日の解説は、以上とします📝

今後も経済学理論集ならびに
社会課題に対する経済学的視点による説明など
有意義な内容を発信できるように努めてまいりますので、今後とも宜しくお願いします🥺

おすすめマガジンのご紹介🔔

こちらのマガジンにて
卒業論文執筆への軌跡
エッセンシャル経済学理論集、ならびに
国際経済学🌏の基礎理論をまとめています

今後、さらにコンテンツを拡充できるように努めて参りますので、今後とも何卒よろしくお願い申し上げます📚

また、こちらに２４卒としての私の就職活動体験記をまとめたマガジンをご紹介させていただきます👍
様々な観点から就職活動について考察していますので、ご一読いただけますと幸いです

改めて、就職活動は
本当に「ご縁」だと感じました🍀

だからこそ、ご縁を大切に
そして、選んだ道を正解にできるよう
これからも努力していきたいなと思います🔥

最後までご愛読いただき誠に有難うございました！

あくまで、私の見解や思ったことを
まとめさせていただいてますが
その点に関しまして、ご了承ください🙏

この投稿をみてくださった方が
ほんの小さな事でも学びがあった！
考え方の引き出しが増えた！
読書から学べることが多い！
などなど、プラスの収穫があったのであれば

大変嬉しく思いますし、投稿作成の冥利に尽きます！！
お気軽にコメント、いいね「スキ」💖
そして、お差し支えなければ
フォロー＆シェアをお願いしたいです👍
今後とも何卒よろしくお願いいたします！