１．概要

１－１．緒言

　本記事は”学習シリーズ”として自分の勉強備忘録用になります。

　本記事ではロジスティック回帰を紹介します。なお、実装のための理解を目的としており厳密な表現は間違っている可能性がありますので、理論は教科書などで学ぶことを推奨します。

１－２．用語・記号の説明（全般）

　本記事で使用する用語および記号は下記の通りです。

　１－２－１．用語一覧

●回帰 (regression)：実数値を予測する問題
●分類 (classification)：カテゴリ（離散値）を予測する問題
●教師あり学習 (supervised learning)：機械学習でデータセットに対して正解値（ラベル）がある学習方法
●教師なし学習 (unsupervised learning)：機械学習でデータセットに対して正解値（ラベル）が無い学習方法
●予測値 (predicted value)：関数で計算された出力変数y（用語は下記参照）
●目標値 (target value)：予測値がとるべき値（教師あり学習の正解値）
●目的関数 (objective function)：機械学習において性能の良さの指標を表す関数です。一般的には”予想値と目標値の差異”から作成される関数であり、この関数を最小化することでよいモデルと判断します。
●多重共線性（multicollinearity）：多変量解析（重回帰分析など）において、いくつかの説明変数間で線形関係（強い相関関係）があると共線性といい、共線性が複数認められる場合は多重共線性があると言います。
●二乗和誤差 (sum-of-squares error)：正解値$${y}$$と予測値$${\hat{y}}$$の差の２乗$${(y-\hat{y})^2}$$です。これをモデルと正解値の誤差とも呼びます。
●最小二乗法：二乗和誤差を最小化することでモデルの当てはまりを最適化する手法です。
●応答変数：目的変数と同義
●線形予測子（linear predictor）：説明変数の一次結合で表されるモデル式（$${{z = β_0 + β_{1}x_{1} + β_{2}x_{2} }}$$）
●リンク関数（link function）：式を変換して線形予測子に対応させる関数->０~１しか取ることのできない確率も線形予測子に対応させること可能となる。また離散値を確率分布として扱える特性もある。
●一般化線形モデル（Generalized Linear Model / GLM）：分散分析と回帰分析を合わせて使う場合のモデル、線形回帰モデルをより柔軟に一般化した統計モデルとも考えられます。
●条件付き確率$${P(B \mid A) = \frac{P(A \cap B)}{P(A)}}$$：条件となる事象Aが起きた場合に、事象Bが起こる確率（※事象AとBが両方とも起こる確率(同時確率)ではないことに注意）
●尤度/尤度関数（likelihood）：母数 θ の各値のもとで，その値がどの程度起りやすいか（確率）をθ の関数として考えたもの

　１－２－２．記号一覧

●$${f()}$$：$${y=f(x)}$$におけるf()であり関数と呼びます。中身は入力変数xを処理して新しい出力変数yを生成する計算式です。
●$${x}$$：$${y=f(x)}$$におけるxです。複数は下記の通り複数あります。
　名称１：説明変数（Explanatory variable）
　名称２：独立変数（Independent variable）
　名称３：外生変数（Exogenous variable）
　名称４：入力変数（Input variable）
　名称５：入力値（Input value）
●$${y}$$：$${y=f(x)}$$におけるyです。複数は下記の通り複数あります。
　名称１：目的変数（Response variable）
　名称２：従属変数（Dependent variable）
　名称３：被説明変数（Explained variable）
　名称４：内生変数（endogenous variable）
　名称５：出力変数（Output variable）
　名称６：予測値/推論値（prediction value）
　名称７：応答変数（response variable）
●$${w_i}$$(weight)：重み（単回帰の場合は傾きとも言う）
●$${b}$$(bias)：バイアス（単回帰の場合は切片とも言う）
●二項係数（組合せ） - binom：異なるn個の物からなる集合があるとき、そのうちのr個を取り出し、順序をつけて一列に並べた時の並べ方のパターン数

$$
\binom{n}{k} = {}_n C_{k} = \frac{n!}{(n-k)!k!}
$$

●要素：集合A(例：母集団)の中に含まれるデータaを要素と呼びます。記号は$${\in}$$を使用し、下記のような記載をします。

$$
aが集合Aの要素：a \in A
$$

$$
(0と1)の2値の要素を持つ集合：x \in \{ 0,1 \}
$$

$$
N×M次元のベクトル： \bf X \in \mathbb{R}^{N \times M }
$$

　１－２－３．ベクトル・行列表記一覧

●M次元の縦ベクトル：$${{\bf x}}$$

$$
\begin{aligned}{\bf x}= \begin{bmatrix} x_{0} \\ x_{1}\\ x_{2} \\ \vdots \\ x_{M} \end{bmatrix} \\ \end{aligned}
$$

●M次元の横ベクトル(縦ベクトルの転置)：$${{\bf x}^{\rm T}}$$

$$
\begin{aligned}{\bf x}^{\rm T}= \begin{bmatrix} x_{0} & x_{1}& x_{2} & \dots & x_{M} \end{bmatrix} & \end{aligned}
$$

●N×M次元の行列(M次元をもつN個のデータ)：$${{\bf X}}$$

$$
\begin{aligned}
{\bf X} &
= \begin{bmatrix} x_{10} & x_{11} & x_{12} & \cdots & x_{1M} \\
x_{20} & x_{21} & x_{22} & \cdots & x_{2M} \\
x_{30} & x_{31} & x_{32} & \cdots & x_{3M} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\ x_{N0} & x_{N1} & x_{N2} & \cdots & x_{NM} \end{bmatrix}
\end{aligned}
=\begin{bmatrix} {\bf x}_1^{\rm T} \\ {\bf x}_2^{\rm T} \\  {\bf x}_3^{\rm T}\\ \vdots \\ {\bf x}_N^{\rm T} \end{bmatrix}
$$

１－３．サンプル用データ：Iris

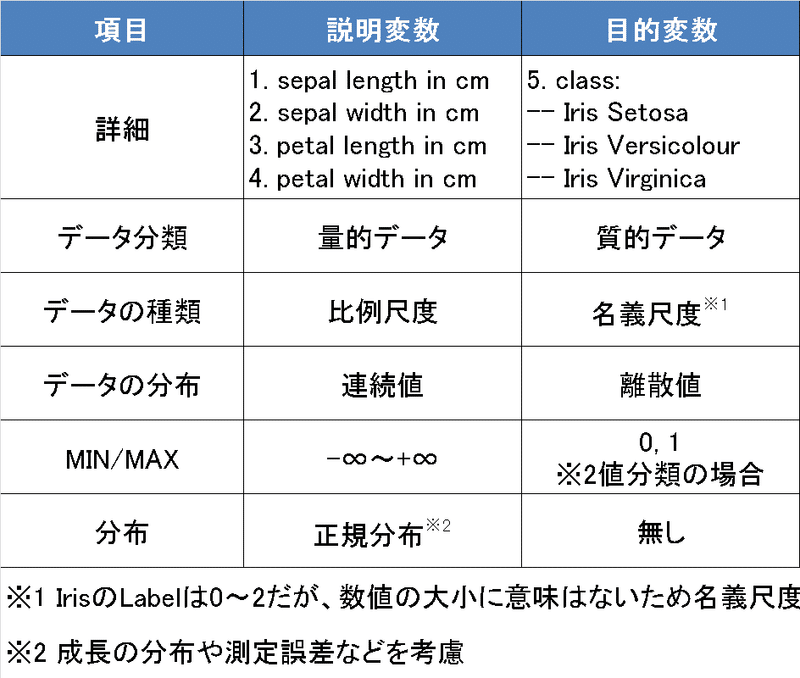
　今回は分類（Classification）のため、サンプルデータはScikit-learnのToy datasetsからIrisデータセットを使用します。

　ロジスティック回帰は多次元の変数を取得可能です。ロジスティック回帰のイメージをつかみやすいように複数パターンで出力しました。

• パターン１：説明変数が１次元×２分類

• パターン２：説明変数が１次元×３分類

• パターン３：説明変数が２次元×２分類

• パターン４：説明変数が２次元×３分類

[IN]
%matplotlib qt
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import os
import glob

from sklearn import datasets


#データセットの読み込み
iris = datasets.load_iris() #irisデータセットの読み込み
data, target = iris.data, iris.target  #データとラベルを取得
data_all = np.concatenate([data, target[:, np.newaxis]], axis=1) #データとラベルを結合 axis=1:列方向
df = pd.DataFrame(data_all, columns=iris.feature_names+['label']) #データフレームに変換
id2label = {i:name for i, name in enumerate(iris.target_names)} #ラベルの辞書

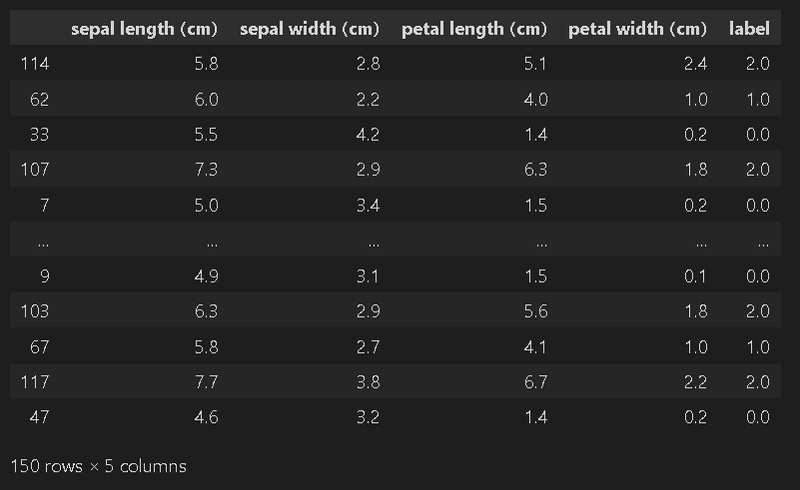
print(df.shape)
print(id2label)

#データ可視化：2次元
fig, axs = plt.subplots(1, 2, figsize=(10, 6), facecolor='w')

df_setosa, df_versicolor, df_virginica = df[df['label']==0], df[df['label']==1], df[df['label']==2]
x1, x2, x3 = df_setosa['sepal length (cm)'], df_versicolor['sepal length (cm)'], df_virginica['sepal length (cm)']
y1, y2, y3 = df_setosa['label'], df_versicolor['label'], df_virginica['label']

#setosaとversicolorのみを抽出
axs[0].scatter(x1, y1, label='setosa', color='r', marker='o')
axs[0].scatter(x2, y2, label='versicolor', color='b', marker='x')
axs[0].set(xlabel='sepal length (cm)', ylabel='label', title='setosa and versicolor')
axs[0].grid(), axs[0].legend()

#3種類のデータをプロット
axs[1].scatter(x1, y1, label='setosa', color='r', marker='o')
axs[1].scatter(x2, y2, label='versicolor', color='b', marker='x')
axs[1].scatter(x3, y3, label='virginica', color='g', marker='^')
axs[1].set(xlabel='sepal length (cm)', ylabel='label', title='Plot of Iris dataset')
axs[1].grid(), axs[1].legend()

#全体のタイトル
fig.suptitle('Iris datasetの2次元プロット', fontsize=20)

#画像の保存
if not os.path.exists('output'): os.mkdir('images') #outputディレクトリがなければ作成
fig.savefig('output/iris_dataset_2d.png')

[OUT]
(150, 5)
{0: 'setosa', 1: 'versicolor', 2: 'virginica'}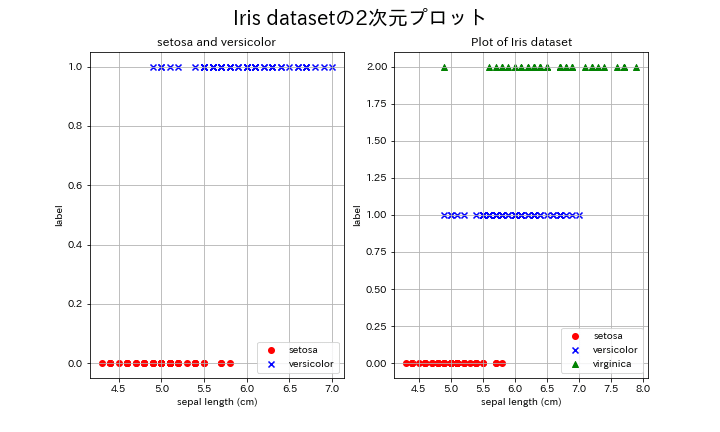

[IN]
#データ可視化：3次元
z1, z2, z3 = df_setosa['label'], df_versicolor['label'], df_virginica['label']
fig = plt.figure(figsize=(10, 10), facecolor='w')
ax = Axes3D(fig)
ax.scatter(x1, y1, z1, label='setosa', color='r', marker='o')
ax.scatter(x2, y2, z2, label='versicolor', color='b', marker='x')
ax.scatter(x3, y3, z3, label='virginica', color='g', marker='^')
ax.set(xlabel='sepal length (cm)', ylabel='sepal width (cm)', zlabel='label', title='Iris datasetの3次元プロット')
plt.show()

[OUT]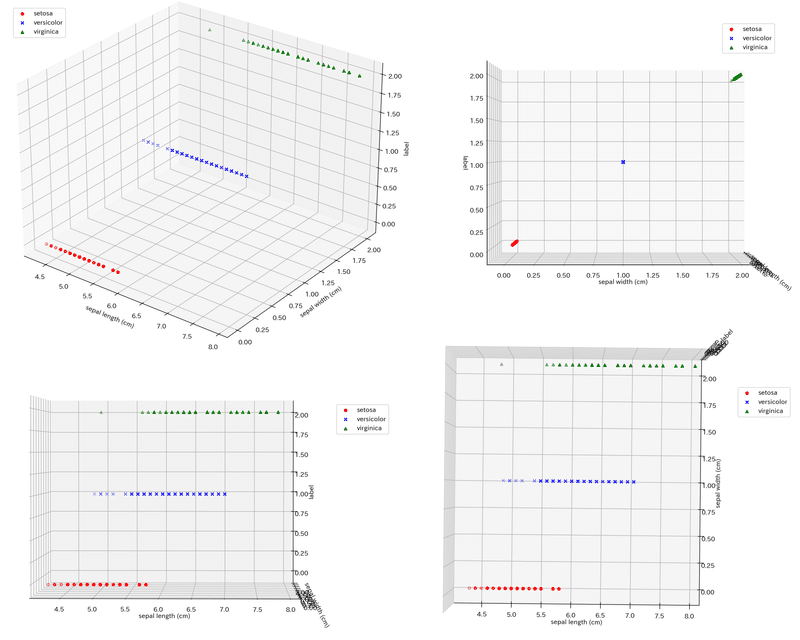

【補足：３Dプロットのinteractive化】
　３DプロットをJupyter内で触れるように"ipympl"をインストールしてコード内に"%matplotlib qt"を追加しました。

[Terminal]
pip install ipympl

２．ロジスティック回帰

２－１．ロジスティック回帰とは

　ロジスティック回帰とは「重回帰の結果を確率に変換した分類モデル」のようなものです。
※おそらく厳密な定義や理論とは異なるかもしれませんが、通常の説明で理解できない場合このように考えるほうが実装には楽です。
　重回帰と同様にモデルの解釈性が非常に高いのが特徴です。一般的には２値分類(2種(0/1)のカテゴリカルデータの分類)に使用されますが、他クラス分類にも適用が可能です。

$$
\begin{aligned}
重回帰：y = w_0 + w_1 x_1 + w_2 x_2 + \cdots + w_n x_n=\sum_{n=0}^{n} w_{n} x_{n}  
\\※x_0=1を追加：w_0x_0=w_0
\end{aligned}
$$

●$${x}$$：入力変数
●$${y}$$：出力変数
●$${w}$$：重み(単回帰での傾き$${a}$$と同等）
●$${w_0}$$：バイアス（単回帰での切片$${b}$$と同等）

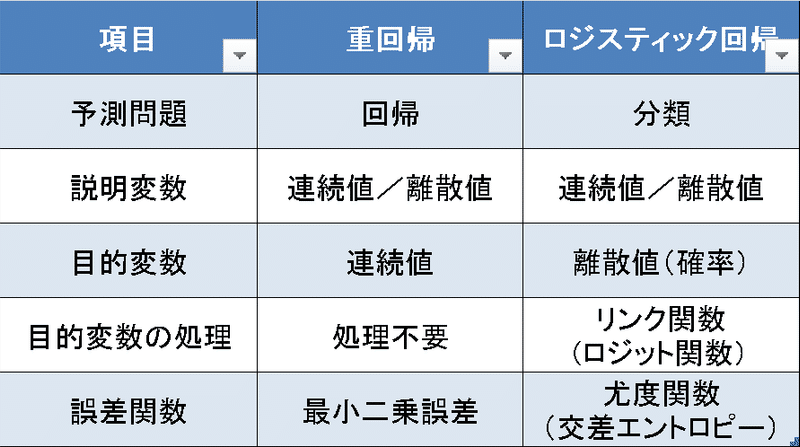
２－２．ロジスティック回帰と重回帰の比較

　ロジスティック回帰と重回帰の比較表は下記の通りです。理解のしやすさを考慮して、ロジスティック回帰は２値分類としています。

３．理論的な数式

　ロジスティック回帰の仕組み及び解法に関して紹介します。全体のフローは下記の通りです。

1. 重回帰の計算結果(線形予測子)を確率と結びつけるためのリンク関数を導入し、ラベル値をとりえる確率$${p}$$を算出

2. 確率$${p}$$を用いてデータセットに最も当てはまりの良さ（尤もらしさ）を表す指標として尤度関数を作成する。

3. その尤度関数が最大化になるようにパラメーターを学習する（最尤推定）

３ー１．リンク関数の適用／確率の計算

　リンク関数の理解と最終出力である確率$${p}$$の計算フローは下記の通りです。

1. データの理解：入力値とラベル値のデータの種類の違い

2. リンク関数の適用：”離散値である目的変数”と”説明変数から計算した線形予測子”を紐づけるため目的変数にリンク関数としてロジット関数を適用

3. 確率$${p}$$の計算：リンク関数を適用した数式を解くことで確率を求める

　３－１－１．データの理解

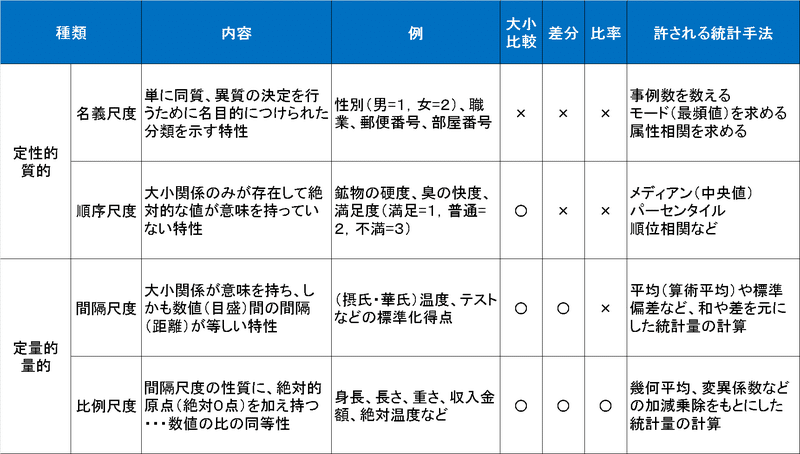
　代表的なデータの分類としては「量的データ」と「質的データ」の２つがあり、また尺度による分け方では「質的データの名義・順序尺度」と「量的データの間隔・比率尺度」として計４種があります。

• 量的データ：数値（定量的）で表せるデータで数値の大小に意味がある

• 質的データ：データの分類や種類の区別（カテゴリカル）に使われ、順位や順序に意味があるデータ

　機械学習モデルとして、重回帰では説明変数$${\bf x}$$と重み$${\bf w}$$（バイアス$${w_0}$$を含む）の内積(線形予測子)を用いて、正解値を推論(目的変数／応答変数)しました。

$$
応答変数t =線形予測子( w_0 + w_1 x_1 + w_2 x_2 + \cdots + w_n x_n)=\bf w^Tx
$$

　しかしクラス分類ではデータの種類を考慮すると下記問題があります。

• 説明変数と目的変数のデータ種類は異なるため同じものとして扱えない

• (2値分類の場合)目的変数の取りえる値が”0と1"に対して線形予測子は-∞~+∞の実数でありのため、推論値（応答変数）とラベル値が対応しない

　３－１－２．リンク関数の適用

　”線形予測子と応答変数が対応していない問題”を解決するために、応答変数にリンク関数を適用します。リンク関数を適用することで応答変数$${y}$$（離散値）が-∞～+∞の連続値へ変換され、線形予測子と同等のものとして扱うことが出来ます。

$$
link(y) =線形予測子( w_0 + w_1 x_1 + w_2 x_2 + \cdots + w_n x_n)
$$

　2値分類ではラベル$${\bf t \in \{0, 1\}}$$、つまり最小値:0, 最大値:1のため推論値(-∞～+∞の連続値)を確率p(0~1)として表現する方がよいです。その変換のために最適なリンク関数がロジット関数です。

$$
\mathrm{logit}(p) = log(odds) = \displaystyle \log({\frac{p}{1-p}})
$$

$$
\log({\frac{p}{1-p}})= w_0 + w_1 x_1 + w_2 x_2 + \cdots + w_n x_n
$$

　下図の通り、ロジット関数は0~1(確率)の値を-∞~+∞へ変換します。なおロジット関数の逆関数は後述する通りシグモイド関数となります。

[IN]
def plotgraph(X, Y, xlabel, ylabel, title, xticks, yticks, verbose=False):
    fig, ax = plt.subplots(figsize=(8, 6), facecolor='white')
    ax.plot(X, Y, label='data')
    ax.set(xlabel=xlabel, ylabel=ylabel, title=title, xticks=xticks, yticks=yticks)
    if verbose:
        x_min, x_max, y_min, y_max = X.min(), X.max(), Y.min(), Y.max()
        ax.plot((x_min, x_max), (0, 0), color='black', lw=1) #x軸
        ax.plot((0, 0), (y_min, y_max), color='black', lw=1) #y軸
        
    ax.grid(), ax.legend()
    plt.show()

def logit(p):
    return np.log(p / (1 - p))

x = np.linspace(0.01, 0.99, 100) 
y = logit(x) #logit関数
plotgraph(x, y, '確率p', 'logit(p)', 'logit関数', np.arange(0, 1.1, 0.1), np.arange(-5, 6, 1), verbose=True)

[OUT]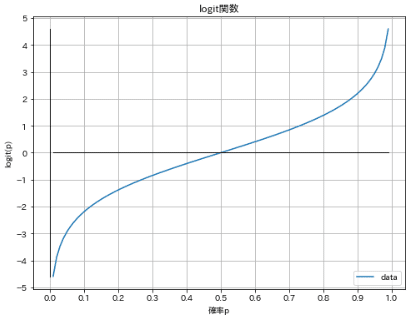

　３－１－３．確率の計算

　線形予測子を$${z}$$とすると、式変形より確率$${p=\dfrac{1}{1+e^{-z}}}$$となります。この式はシグモイド関数と同じになります。

$$
\begin{aligned}
z=\log\dfrac{p}{1-p} \\
e^z=\dfrac{p}{1-p} \\
e^z-e^zp=p \\
p=\dfrac{e^z}{e^z+1} =\dfrac{1}{1+e^{-z}}
\end{aligned}
$$

　これより、線形予測子 $${z}$$ と目的変数 $${y}$$の関係を表現するロジスティック回帰モデルが導出され、線形予測子 $${z}$$ から目的変数 $${y}$$の確率を算出できます。
　なおラベル$${\bf t \in \{0, 1\}}$$のため、確率$${p}$$はt=0とt=1の2値の確率を計算します。

$$
p(t|x_1, x_2, ..., x_n)
=\frac{1}{1 + e^{-z}}
= \frac{1}{1 + e^{-( w_0 + w_1 x_1 + w_2 x_2 + \cdots + w_n x_n)}}
$$

【参考：記号の意味】
　上記で使用した$${p(t|x_1, x_2, ..., x_n)}$$は条件付き確率の標記であり、意味は下記の通りです。

• $${p(t|x_1, x_2, ..., x_n)}$$：説明変数$${\bf x=x_1, x_2, ..., x_n}$$においてラベル値が$${y}$$である確率

• $${p(t=1|x_1, x_2, ..., x_n)}$$：説明変数$${\bf x=x_1, x_2, ..., x_n}$$においてラベル値が$${y=1}$$である確率

• $${p(t=0|x_1, x_2, ..., x_n)}$$：説明変数$${\bf x=x_1, x_2, ..., x_n}$$においてラベル値が$${y=0}$$である確率

３－２．尤度関数：モデルの目的関数

　ここからはロジスティック回帰の重みとバイアスを更新して最適なパラメータを求めていきます。
　説明変数$${\bf x}$$、目的変数$${\bf y}$$共に実数の連続値では、重回帰による「二乗誤差$${({\bf t} - {\bf y})^{\rm T}({\bf t} - {\bf y})}$$を最小にする重み・バイアスを探索(モデルの学習)」しました。しかし２値分類では下記問題があります。

• $${\bf y=w^Tx}$$の出力は-∞~+∞のため0~1の出力にならない：学習データで0~1に入れたとしてもテストデータでは説明変数は不明のため、意味のない結果が出力される可能性がある(特定の数値前後でラベルが0,1に変化する場合、重回帰だとある数値以上では誤差が増える方向になる。

[IN]
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression, LogisticRegression

X = np.array([1, 2, 3, 4, 5])
Y = np.array([0, 0, 1, 1, 1])
# 最小二乗法による回帰分析
model1 = LinearRegression().fit(X.reshape(-1,1), Y)
y_pred = model1.predict(X.reshape(-1,1))
diffs = Y - y_pred # 残差

# 可視化
fig, ax = plt.subplots(1,1, figsize=(7,7), facecolor='w')
sns.set(style="darkgrid")
plt.scatter(X, Y)
# ロジスティック回帰による分類の可視化
ax.plot(X, Y, 'o', label="data", c='red')
ax.plot(X, y_pred, '-', label="logistic regression", c='blue', lw=1.0)
ax.set(xticks=X.flatten(), xlabel="x", ylabel="y", title="Logistic Regression")
#残差を両矢印で表示
for idx, diff in enumerate(diffs):
    ax.annotate("", xy=(X[idx], y_pred[idx]), xytext=(X[idx], Y[idx]), arrowprops=dict(arrowstyle="<->", color='blue'))
    ax.text(X[idx]+0.2, (Y[idx]+y_pred[idx])/2, f'{diff:.2f}', ha='center', va='center', color='blue')

ax.legend()
plt.show()

[OUT]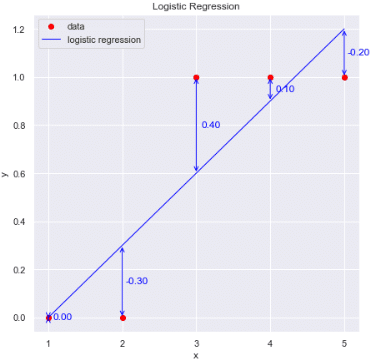

　リンク関数を使用して線形予測子 $${z}$$ を確率$${p}$$で表現しているため、は「尤度関数を最大化する重み・バイアスを探索」します。
　ロジスティック関数のパラメータ最適化手順は下記の通りです。

1. 尤度関数を定義

2. 対数尤度関数に変換：尤度関数の両辺を対数で取得

3. 勾配降下法が使用できるよう、対数尤度関数の式にマイナスをかける：マイナスした関数の最小化を目的とする

4. 勾配降下法でパラメーターを更新

　３－２－１．尤度関数の定義

　尤度 (likelihood) とは”データに対してパラメータの尤もっと もらしさ”を示す指標であり「あるデータが与えられたときに、モデルのパラメータがどの程度良く当てはまるかを表す尺度」です。別の表現をすると「そのデータが生成される確率->データの正解度合い->パラメータの適切さ」ともいえると思います。

尤度はパラメータ（重み・バイアス）の関数として表すことができ、その関数を尤度関数と呼びます。尤度関数$${L(w)}$$の定義および特徴は下記の通りです。

• 尤度関数$${L(w)}$$は各データにおける※尤度$${p(y^{(i)} | x^{(i)},w)}$$の掛け算で表されている（※$${p(y^{(i)} | x^{(i)},w)}$$パラメータ$${w}$$が与えられたとき、データ$${x_i}$$がクラス$${y_i}$$に属する条件付き確率とも言えます）

• 「尤度が高い=そのデータの正解値の確率が高い」とすると、尤度関数$${L(w)}$$は全データの尤度の総乗のため、全データにおける正解値の当てはまりと考えることが出来る。

• 尤度関数$${L(w)}$$を最大化することは、全データに対する当てはまりが最適（尤もらしい）ことを意味している

$$
L(w) = \prod_{i=1}^n p(y^{(i)} | x^{(i)},w)
=p(y^{(1)} | x^{(1)},w) \times p(y^{(2)} | x^{(2)},w) \cdots \times p(y^{(n)} | x^{(n)},w)
$$

$$
L(w) = \prod_{i=1}^n(各データの尤度)=尤度_{データ1} \times 尤度_{データ2} \cdots 尤度_{データn}
$$

• $${n}$$：データセット内のサンプル数(データ数)

• $${i}$$：$${i}$$行目のデータ

• $${w}$$：モデルのパラメータ（重み, バイアス）

• $${x^{(i)}}$$：説明変数（入力特徴量）

• $${y^{(i)}}$$($${y \in \{0, 1\}}$$)：ラベルデータ(対応する出力)->2値のため0または1（※別箇所で$${t}$$を使用しましたがここでは$${y}$$を使用）

• $${p(y^{(i)} | x^{(i)},w)}$$：各データの尤度

　ラベル値$${y \in \{0, 1\}}$$は0か1の値しかとらないため、各データの尤度$${p(y^{(i)} | x^{(i)},w)}$$はy=0かy=1の2つの確率を取ります。2値より片方の確率を$${p}$$とするともう片方の確率は$${1-p}$$となります。y=1の確率をリンク関数経由で式変形したものを適用するとy=1, y=0の確率は下記の通りです。

$$
p_i = p(y^{(i)} =1 | x^{(i)},w) = \dfrac{1}{1+\exp(-z)}
$$

$$
p_i = p(y^{(i)} =0 | x^{(i)},w) = 1 - p(y^{(i)} =1 | x^{(i)},w) = \dfrac{\exp(-z)}{1+\exp(-z)}
$$

$$
p(y^{(i)} | x^{(i)},w) = (p_i)^{y^{(i)}}(1-p_i)^{1-y{(i)}}
$$

　$${p(y^{(i)} | x^{(i)},w) = (p_i)^{y^{(i)}}(1-p_i)^{1-y{(i)}}}$$とするとy=0, y=1の条件における尤度を一つの式として表すことが出来ます。よって尤度関数$${L(w)}$$は下記の通りとなります。

$$
L(w) = \prod_{i=1}^n p(y^{(i)} | x^{(i)},w)
= \prod_{i=1}^n \left(p_i\right)^{y^{(i)}} \left(1-p_i\right)^{1-y^{(i)}}
$$

　参考までにy=0, 1における尤度を記載しました。各ラベル値$${y \in \{0, 1\}}$$で線対称になっていることが確認できます。

[IN]
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib

#p(y=1|z)の尤度関数
def prob1(z):
    return 1 / (1 + np.exp(-z)) #z:線形予測値(w^TX)
#p(y=0|z)の尤度関数
def prob0(z):
    return 1 - prob1(z) #1-p(y=1|z)=exp(-z)/(1+exp(-z))

def likelihood(z, y):
    return prob1(z)**y * prob0(z)**(1-y)  #尤度関数 
#線形予測子z=w^TXを想定
z = np.linspace(-10, 10, 100)
#尤度関数の計算
likelihood_y0 = likelihood(z, 0) #y=0の尤度関数
likelihood_y1 = likelihood(z, 1) #y=1の尤度関数

#可視化
fig = plt.figure(figsize=(8, 6), facecolor='w')
plt.plot(z, likelihood_y0, label=r'$L(z|y=0)=\frac{e^{-z}}{1+e^{-z}}$', c='red')
plt.plot(z, likelihood_y1, label=r'$L(z|y=1)=\frac{1}{1+e^{-z}}$', c='blue')
plt.xlabel('線形予測子z', fontsize=12), plt.ylabel('尤度関数L', fontsize=12)
plt.title(r'ロジスティック回帰の尤度関数：$L(z|y)=(\frac{1}{1+e^{-z}})^y (\frac{e^{-z}}{1+e^{-z}})^{1-y}$', fontsize=16, y=-0.18)
plt.grid()
plt.legend(fontsize=14)
plt.show()

[OUT]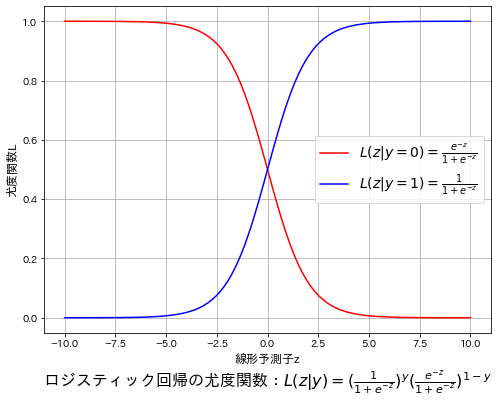

　３－２－２．補足１：尤度関数の理解

　前項より、尤度関数$${L(w)}$$に関して下記のことが確認できました。

1. 尤度関数は確率（各データの尤度）の総乗で計算されるため最大値は1、最小値は0となる。

2. 尤度が高いほど当てはまりが良い（パラメータで正解を予測できている）ため、「各データの尤度の掛け算が高い＝最低なパラメータである」と理解できる

3. 確率（尤度）$${ p(y^{(i)} | x^{(i)},w)}$$は説明変数：$${x}$$、ラベル：$${y \in \{0, 1\}}$$、モデルのパラメータ：$${w}$$からなる。

4. $${x}$$, $${y}$$は固定値（データ）のため、尤度関数はパラメータ$${w}$$によって変化する

5. パラメータをうまく変化させれば最適な尤度が計算できる（最尤推定）。

　つまり尤度関数はパラメータによって確率が変化する関数であり、パラメータを変更すると確率分布に似た分布が取得できます（尤度関数は確率の総乗であるため、確率分布や確率密度関数とは異なります）。
　データから得られる確率が最大になるパラメータを推定する（最尤推定）ことで、最適値を選定できます。

　３－２－３．補足２：最小二乗法と最尤推定の違い

　重回帰では最小二乗法を使用しましたが、ロジスティック回帰ではラベル値$${y \in \{0, 1\}}$$の確率を求めるため、確率モデルである尤度関数の方が最適です。
　違いも含めた比較表は下記の通りです。

$$
\begin{array}{l:l:l}
\textbf{項目} & \textbf{最小二乗法} & \textbf{最尤推定} \\ \hline
目的関数 & 誤差の2乗 & 尤度関数\\
モデルの種類 & 決定論モデル?? & 確率論モデル\\
目的関数の意味 &推論値とラベルの誤差 & パラメータの尤もらしさ \\
数式 & Loss= \sum_{i=1}^n (y_i - f(x_i))^2 &L(w)= \prod_{i=1}^n f(x_i)^{y_i} (1-f(x_i))^{1-y_i} \\
パラメータ & 重み・バイアス：\bf w^T& 重み・バイアス：\bf w^T\\
パラメータの最適化& 誤差の2乗を最小化& 尤度関数を最大化 \\
最適化手法& 勾配降下法 & 勾配降下法 \\
目的関数の範囲 & 実数全体(-∞～∞) & 0～1 \\
目的関数の最適値 & Loss=0& L(w)=1\\
\end {array}
$$

　３－２－４．補足３：最尤推定の練習問題

　サンプル問題を解きながら尤度関数／最尤推定を理解していきます。参考として「英語と数学の点数から大学の合否判定」の問題を解いていきます。データは適当に作成しました。
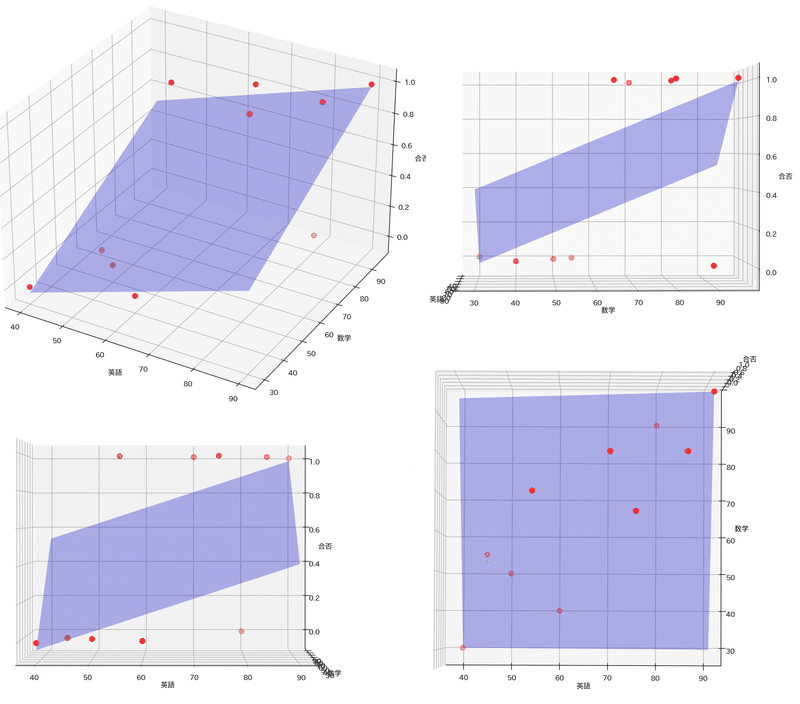
　まずは重回帰で表現しましたが、十分にモデルを表現できておりません。

$$
\bf X= \begin{bmatrix}
70 & 80 \\
75 & 65 \\
80 & 90 \\
60 & 40 \\
45 & 55 \\
55 & 70 \\
90 & 95 \\
85 & 80 \\
40 & 30 \\
50 & 50 \\
\end{bmatrix},
t=\begin{bmatrix}
1 \\1 \\0 \\0 \\0 \\1 \\1 \\1 \\0 \\0 \\
\end{bmatrix}
$$

[IN]
%matplotlib qt
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
from mpl_toolkits.mplot3d import Axes3D
from sklearn.linear_model import LinearRegression
from scipy.optimize import minimize

# データの読み込み
data = np.array([[70, 80, 1],
                 [75, 65, 1],
                 [80, 90, 0],
                 [60, 40, 0],
                 [45, 55, 0],
                 [55, 70, 1],
                 [90, 95, 1],
                 [85, 80, 1],
                 [40, 30, 0],
                 [50, 50, 0]])

df = pd.DataFrame(data, columns=['英語', '数学', '合否'])
display(df.T)

X = data[:, :-1]  # 説明変数
y = data[:, -1]   # 目的変数

#重回帰で表現
linear = LinearRegression() #インスタンス化
linear.fit(X, y) #学習
y_pred_linear = linear.predict(X) #予測


#重回帰を可視化
fig = plt.figure(figsize=(10, 10), facecolor='w')
ax = Axes3D(fig)
ax.scatter(X[:, 0], X[:, 1], y, c='r', marker='o', label='ラベル', s=50)

x_min, x_max, y_min, y_max = X[:, 0].min(), X[:, 0].max(), X[:, 1].min(), X[:, 1].max()
X_mesh, y_mesh = np.meshgrid(np.linspace(x_min, x_max, 100), np.linspace(y_min, y_max, 100))
Z = linear.predict(np.c_[X_mesh.ravel(), y_mesh.ravel()])

ax.plot_surface(X_mesh, y_mesh, Z.reshape(X_mesh.shape), alpha=0.3, color='b')
ax.set(xlabel='英語', ylabel='数学', zlabel='合否')
plt.grid(), plt.legend()
plt.show()

[OUT]
スペースの都合上、転置して表示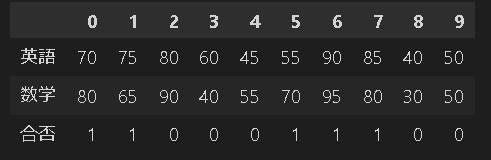

　尤度関数/対数尤度関数は下記式となります。$${p_i}$$は確率(尤度)の推定値,、$${y_i \in \{0,1\}}$$は2値の正解ラベルです。

$$
L(\beta) = \prod_{i=1}^{n} p_i^{y_i}(1-p_i)^{1-y_i}
$$

$$
\ln L(w) = \sum_{i=1}^{n} y_i\ln(p_i) + (1-y_i)\ln(1-p_i)
$$

　yに実際の値(0, 1)を代入してみると下記の通りであり、確率が正解ラベルに近いほど高い値をとることが分かります。つまり、推論した確率が(0, 1)に近いほど尤度関数の値が高くなります。

• y=0の時：$${p_i^{y_i}(1-p_i)^{1-y_i}}$$=$${(1-p_i)}$$より、$${p_i}$$は0に近いほど高い値となる

• y=1の時：$${p_i^{y_i}(1-p_i)^{1-y_i}}$$=$${p_i}$$より、$${p_i}$$は1に近いほど高い値となる

　対数尤度関数もグラフ化してどのような挙動になるか確認しました。

• y=0の時：$${ y_i\ln(p_i)=0}$$であり、全体の式は$${(1-y_i)\ln(1-p_i)=\ln(1-p_i)}$$となるためx=0でy=0, x=1でy=－∞となる。

• y=1の時：$${(1-y_i)\ln(1-p_i)=0}$$であり、全体の式は$${ y_i\ln(p_i)=\ln(p_i)}$$となるためx=1でy=0, x=0でy=－∞となる

• 上記より、確率pが正解ラベルの値に近いほど対数尤度関数の合計は最大化されます。よって尤度関数／対数尤度関数を最大化＝正解数が多い＝最適なパラメータ選定となります。

[IN]
%matplotlib inline
p=np.linspace(0.01, 1, 100) #0.01~1の範囲で100個のデータを作成
y0, y1 = 0, 1 #ラベル値

plt.figure(figsize=(8, 6), facecolor='w')
plt.plot(p, y0*np.log(p) , label='ylog(p), y=0', c='red')
plt.plot(p, (1-y0)*np.log(1-p) , label='(1-y)log(1-p), y=0', c='red', ls='--')
plt.plot(p, y1*np.log(p) , label='ylog(p), y=1', c='blue')
plt.plot(p, (1-y1)*np.log(1-p) , label='(1-y)log(1-p), y=1', c='blue', ls='--')
plt.xlabel(r'確率$p$', fontsize=12)
plt.ylabel(r'$ylog(p)$+$(1-y)log(1-p)$', fontsize=12)
plt.grid(), plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0, fontsize=12)
plt.title('対数尤度関数', fontsize=12, y=-0.16)
plt.show()

[OUT]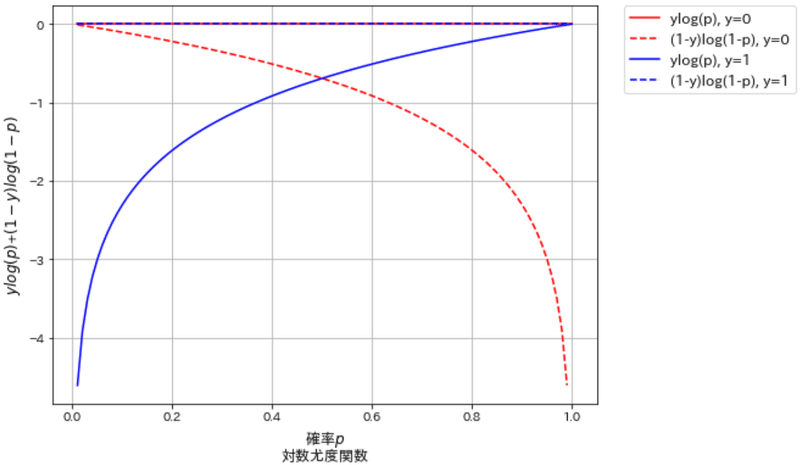

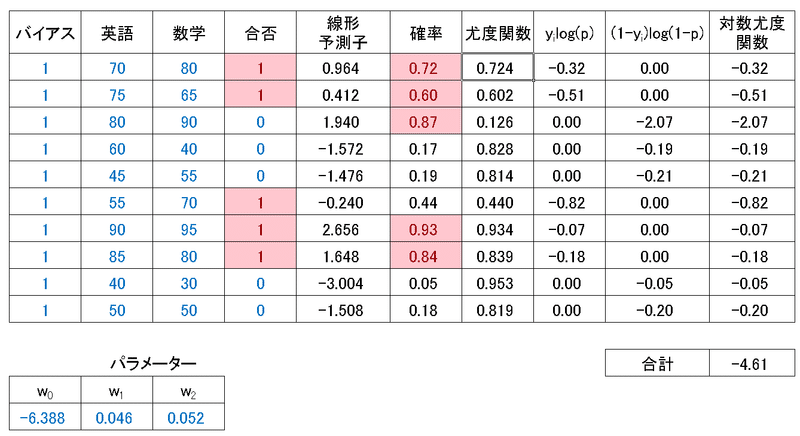
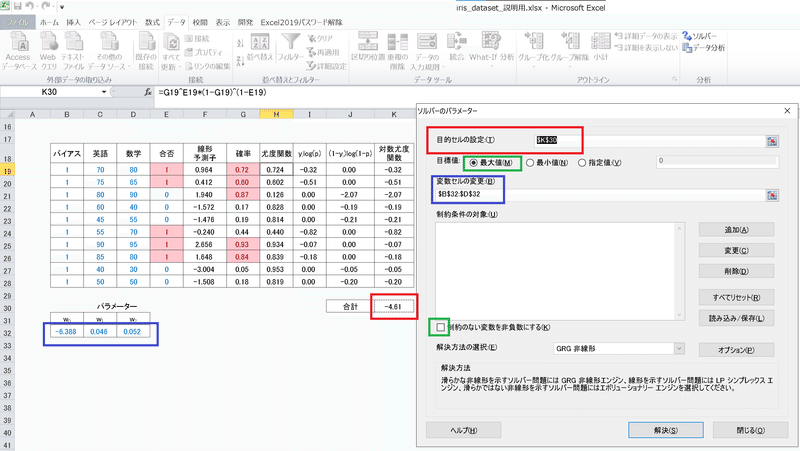
　PythonでのコードとExcelでの計算結果を示します。Excelの計算は下記手順で実施しました。

• 説明変数$${\bf X}$$にバイアス項の列：1を追加する

• 重みとバイアス：$${\bf w^T=\begin{bmatrix}w_0 & w_1 & w_2\end{bmatrix}}$$を追加：初期値は適当に設定

• 線形予測子$${z=\bf w^TX}$$を計算

• 線形予測子をシグモイド関数$${\frac{1}{1+e^{-z}}}$$に通して確率に変換

• $${\ln L(\beta) = \sum_{i=1}^{n} y_i\ln(p_i) + (1-y_i)\ln(1-p_i)}$$：各行の対数尤度関数を計算してその合計値を取得

• Excelのソルバーを使用して$${\ln L(\beta) }$$を最大化（※ソルバーには最大化の機能があるため反対符号をとって勾配降下法は不要）

[IN]
from sklearn.linear_model import LogisticRegression

log = LogisticRegression()
log.fit(X, y)
print(log.predict(X))
print(f'Weight\n{log.coef_}', f'bias\n{log.intercept_}', sep='\n')

[OUT]
[1 1 1 0 0 0 1 1 0 0]
Weight
[[0.04551016 0.05192708]]
bias
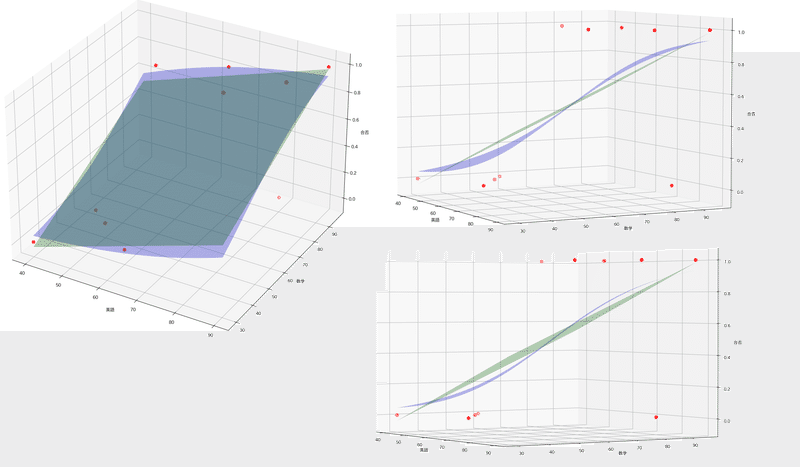
[-6.37705906]

　最後にロジスティック回帰をプロットしました。重回帰では単純な平面ですがロジスティック回帰ではゆがんだ空間（超平面）を生成していることが確認できました。

[IN]
#ロジスティック回帰で表現
weights = np.array([-6.37705906, 0.04551016, 0.05192708])
def sigmoid(x):
    return 1 / (1 + np.exp(-x))
X_with_bias = np.c_[np.ones((X_mesh.ravel().shape[0], 1)), X_mesh.ravel(), y_mesh.ravel()]
_Z_proba = np.dot(X_with_bias, weights)
Z_proba = sigmoid(_Z_proba)

#重回帰を可視化
fig = plt.figure(figsize=(10, 10), facecolor='w')
ax = Axes3D(fig)
ax.scatter(X[:, 0], X[:, 1], y, c='r', marker='o', label='ラベル', s=50)

x_min, x_max, y_min, y_max = X[:, 0].min(), X[:, 0].max(), X[:, 1].min(), X[:, 1].max()
X_mesh, y_mesh = np.meshgrid(np.linspace(x_min, x_max, 100), np.linspace(y_min, y_max, 100))
ax.plot_surface(X_mesh, y_mesh, Z_proba.reshape(X_mesh.shape), alpha=0.3, color='b')
# ax.plot_surface(X_mesh, y_mesh, Z.reshape(X_mesh.shape), alpha=0.3, color='b') #重回帰の結果を重ねる

ax.set(xlabel='英語', ylabel='数学', zlabel='合否')
plt.grid(), plt.legend()
plt.show()

[OUT]

【ロジスティック回帰のみ】

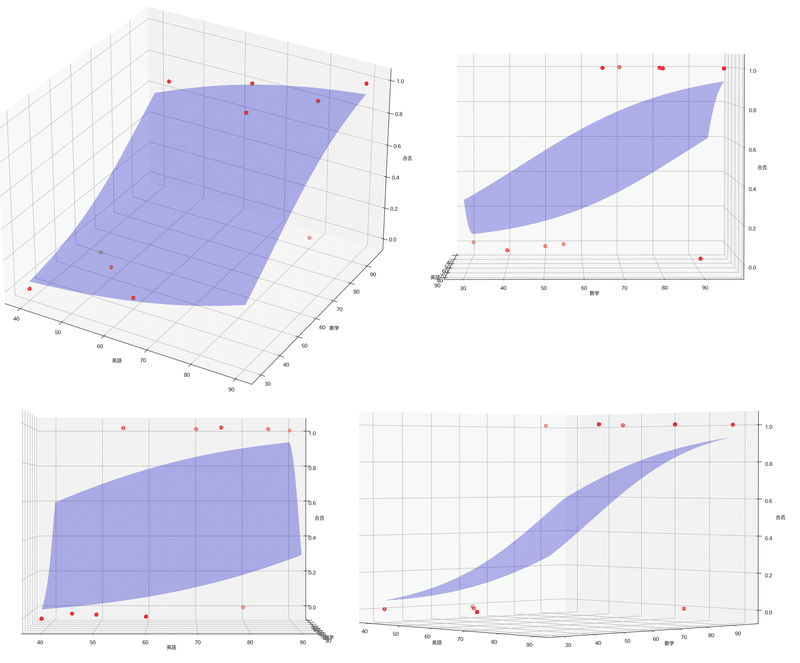
【ロジスティック回帰＋重回帰】

　３－２－５．補足４：尤度関数の可視化

　最尤推定は「尤度関数が最大化するパラメータの探索」でした。それの意味を可視化してみます。

$$
\begin{array}{l:l:l}
\textbf{項目} & \textbf{最小二乗法} & \textbf{最尤推定} \\ \hline
目的関数 & 誤差の2乗 & 尤度関数\\
モデルの種類 & 決定論モデル?? & 確率論モデル\\
目的関数の意味 &推論値とラベルの誤差 & パラメータの尤もらしさ \\
数式 & Loss= \sum_{i=1}^n (y_i - f(x_i))^2 &L(w)= \prod_{i=1}^n f(x_i)^{y_i} (1-f(x_i))^{1-y_i} \\
パラメータ & 重み・バイアス：\bf w^T& 重み・バイアス：\bf w^T\\
パラメータの最適化& 誤差の2乗を最小化& 尤度関数を最大化 \\
最適化手法& 勾配降下法 & 勾配降下法 \\
目的関数の範囲 & 実数全体(-∞～∞) & 0～1 \\
目的関数の最適値 & Loss=0& L(w)=1\\
\end {array}
$$

　可視化するには2・3次元の必要があるため先ほどのデータを1次元に変更しました(英語のデータと合格のデータセット)。計算時にはバイアス項が入るため1の列を追加します。

$$
\bf X= \begin{bmatrix}70  \\75  \\80  \\60  \\45  \\55  \\90  \\85  \\40  \\50  \\\end{bmatrix}
, t=\begin{bmatrix}1 \\1 \\0 \\0 \\0 \\1 \\1 \\1 \\0 \\0 \\ \end{bmatrix}
, \bf X_{bias} = \begin{bmatrix}1 &70  \\1 &75  \\1 &80  \\1 &60  \\1 &45  \\1 &55  \\1 &90  \\1 &85  \\1 &40  \\1 &50  \\\end{bmatrix}
$$

[IN]
data_1dim = np.array([[70, 1],
                    [75, 1],
                    [80, 0],
                    [60, 0],
                    [45, 0],
                    [55, 1],
                    [90, 1],
                    [85, 1],
                    [40, 0],
                    [50, 0]])

#データにバイアスを追加
_ones_bias = np.ones((data_1dim.shape[0], 1))
datas = np.concatenate([_ones_bias, data_1dim[:, :-1]], axis=1) #バイアス項用の1を追加
target = data_1dim[:, -1] #ラベル

# ロジスティック回帰モデルの定義：回答確認
log = LogisticRegression()
log.fit(data_1dim[:, :-1], data_1dim[:, -1])
print(log.predict(data_1dim[:, :-1]))
print(f'slope\n{log.coef_}', f'intercept\n{log.intercept_}', sep='\n')

[OUT]
[1 1 1 0 0 0 1 1 0 0]
slope
[[0.09370268]]
intercept
[-6.0906743]

　これより重み$${w_1=0.09}$$, $${w_0=-6.09}$$となりました。この結果は尤度関数の最大値（負の対数尤度関数の最小値）を求めてパラメータ$${\bf w^T=\begin{bmatrix} w_0 & w_1 \end{bmatrix}}$$を最適化したことで求めることが出来ました。
　それでは尤度関数がどのような分布になっているか確認します。結果としてパラメータ$${\bf w^T=\begin{bmatrix} w_0 & w_1 \end{bmatrix}}$$に対して山のような形状になっており

[IN]

def linear_reg(X, w):
    return np.dot(X, w) #内積で線形予測値を計算

def sigmoid(x):
    return 1 / (1 + np.exp(-x)) #シグモイド関数

# 尤度関数の定義
def calc_likelihood(prob, label):
    likelihood = prob ** label * (1 - prob) ** (1 - label) #p^y(1-p)^(1-y)
    return likelihood

# 各重みにおける尤度関数の計算・配列化
slopes = np.linspace(-10, 10, 100)
intercepts = np.linspace(-10, 10, 100)
S, I = np.meshgrid(slopes, intercepts) #各重みにおける尤度関数の計算・配列化

outputs = [] #尤度関数を格納する配列

#slopes:100×intercepts:100=10000通りの重みの組み合わせを計算※zip()をそのまま使うと100通りになるため注意
for intercept in intercepts:
    for slope in slopes:
        w = np.array([intercept, slope]) #重みを[intercept, slope]の順に並べる
        linear_pred = linear_reg(datas, w) #線形予測値
        prob = sigmoid(linear_pred) #確率
        likelihoods = calc_likelihood(prob, target) #各データ尤度
        likelihood_func = np.prod(likelihoods)  #尤度関数         outputs.append(likelihood_func) #尤度関数を配列に追加
    
Z = np.array(outputs) #尤度関数の配列
Zs = Z.reshape(S.shape) #尤度関数の配列をグラフ用に整形(100×100)

#グラフの描画
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(10, 10), facecolor='w')
ax = fig.gca(projection='3d')

#尤度関数のプロット
surf = ax.plot_surface(S, I,  Zs , cmap='coolwarm', alpha=0.8)

#x, y軸のラベルとタイトルの設定
ax.set_xlabel('slope')
ax.set_ylabel('intercept')
ax.set_zlabel('Likelihood')
ax.set(title='Logistic Regression Likelihood Surface',
       xticks=np.arange(-10, 10, 1), yticks=np.arange(-10, 10, 1))
plt.title('Logistic Regression Likelihood Surface')

#カラーバーの表示
fig.colorbar(surf)
plt.show()

[OUT]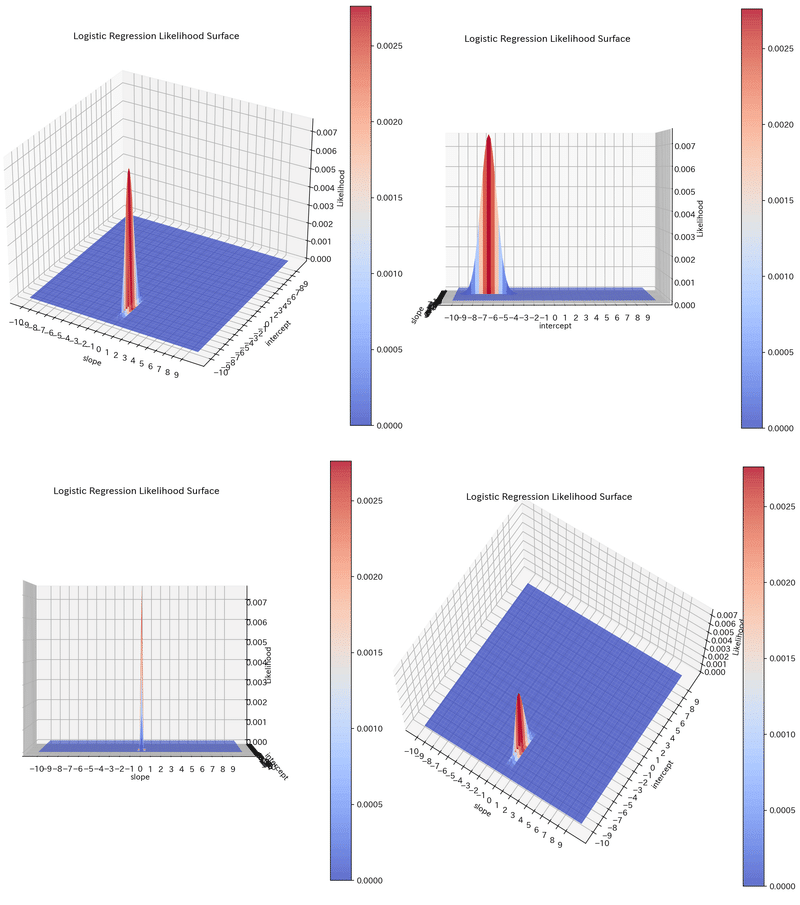

　"ax.contour"による等高線も描写してみました。

[IN]
%matplotlib inline
# 等高線図の描画
fig, ax = plt.subplots(figsize=(8, 8), facecolor='w')
# 等高線のプロット
CS = ax.contour(S, I, Zs, levels=10, cmap='coolwarm')

# 等高線のラベルの設定
ax.clabel(CS, inline=True, fontsize=10)

# 軸ラベルとタイトルの設定
ax.set_xlabel('slope', fontsize=12)
ax.set_ylabel('intercept', fontsize=12)
ax.set_title('Logistic Regression Likelihood Surface', fontsize=14)
ax.set(xticks=np.arange(-10, 10, 1), yticks=np.arange(-10, 10, 1))
# グリッド表示
ax.grid(True)
plt.show()

# 等高線図の描画
fig, ax = plt.subplots(figsize=(8, 8), facecolor='w')
# 等高線のプロット
CS = ax.contour(S, I, Zs, levels=10, cmap='coolwarm')

# 等高線のラベルの設定
ax.clabel(CS, inline=True, fontsize=10)

# 軸ラベルとタイトルの設定
ax.set_xlabel('slope', fontsize=12)
ax.set_ylabel('intercept', fontsize=12)
ax.set_title('Logistic Regression Likelihood Surface', fontsize=14)
ax.set(xticks=np.arange(-2, 2, 0.5), yticks=np.arange(-9, -4, 0.5), xlim=(-2, 2), ylim=(-9, -4))
# グリッド表示
ax.grid(True)
plt.show()

[OUT]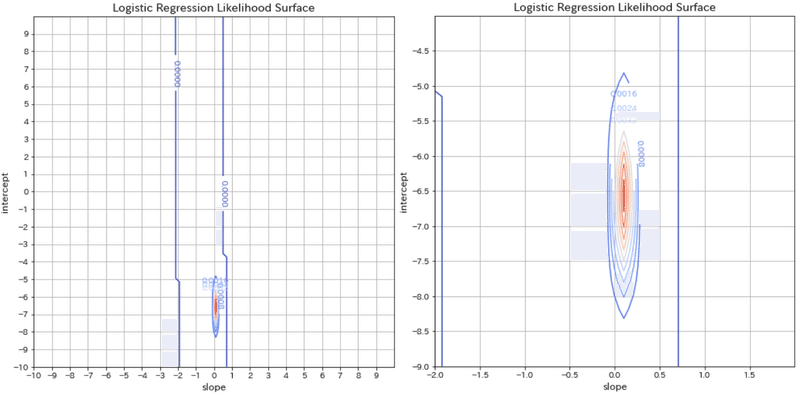

３－３．最尤推定：最適なパラメータの探索

　前項より、尤度関数を最大化は全データに対するパラメータの尤もらしさを最適化します。尤度関数が最大となるパラメータを見つけることを最尤推定と言います。
　尤度関数を最大化したいのですが$${L(w) = \prod_{i=1}^n p(y^{(i)} | x^{(i)},w)}$$のままだと（特に微分の）計算が手間であり、かつ確率の掛け算(総乗)のためアンダーフロー(値が小さすぎてPCが計算できない)の問題があります。
　この問題を解決するため尤度関数を対数で取ることで総乗(積)$${\prod}$$を合計（和）$${\sum}$$に変換できます。

$$
LL(w)= log(\prod_{i=1}^n p(y^{(i)} | x^{(i)},w))
=log( \prod_{i=1}^n \left(p_i\right)^{y^{(i)}} \left(1-p_i\right)^{1-y^{(i)}})
$$

$$
LL(w)=\sum_{i=1}^n [y^{(i)}log(p^{(i)}) + (1-y^{(i)})log(1-p^{(i)})]  
$$

　対数尤度関数は解析解をもたないため数値最適アルゴリズムを使用する必要があり、一般的には勾配降下法を使用します。勾配降下法では最小値を求めるため、対数尤度関数の符号を反転させることで最小値を求める形に変換することができ、変換した関数をBinary Cross Entropy（二値交差エントロピー）と呼びます。
　これらが計算出来たら下記手順でパラメータを学習します。

1. 尤度関数を対数化(対数尤度関数）

2. 対数尤度関数の符号を反転して損失関数（BCE）を算出

3. 損失関数（BCE）の微分を計算

4. 勾配降下法によりパラメータを学習

【損失関数(誤差関数)：二値交差エントロピー】

$$
-LL(w)=BCE(y,t​)=− \sum_{i=1}^n(t_{i}logy_{i}​ + (1−t_{i})log(1−y_{i}​))
$$

$$
t_{i}\in \{0,1\}：ラベル値,  y_{i} ：モデルの推論値(確率0～1)
$$

【勾配降下法】

$$
w_i \leftarrow w_i - \eta\frac{\partial BCE(}{\partial w_i}
$$

$$
b \leftarrow b - \eta \frac{\partial BCE}{\partial b}
$$

$${w_i}$$：$${i}$$番目の重み、$${b=w_0}$$：バイアス、$${\eta}$$：学習率

【損失関数の微分】
※BCEに$${\frac{1}{N}}$$を追加

$$
\frac{\partial BCE}{\partial w} =\frac{1}{N} \sum_{i=1}^N \left(t_i - y_i \right) x_i
$$

【参考：微分式の導出】

$$
z = \bf w^T x_i , \bf w^T=\begin{bmatrix}w_0 & w_1 & w_2 \cdots & w_n\end{bmatrix}
$$

$$
y_i = \sigma(z) = \frac{1}{1 + e^{-z}}
$$

$$
\begin{aligned}
\frac{\partial y_i}{\partial w}
=\frac{\partial y_i}{\partial z} \cdot \frac{\partial z}{\partial w}
&= \frac{\partial}{\partial z} \left( \frac{1}{1 + e^{-z}} \right) \cdot \frac{\partial z}{\partial w} \\
&=y_i(1-y_i)\cdot x_i
\end{aligned}
$$

　上記の式変形は下記を使用しました。

$$
\begin{aligned}
\frac{d}{dx} \sigma(x)
= \frac{d}{dx} \left( \frac{1}{1 + e^{-x}} \right) = \frac{e^{-x}}{(1 + e^{-x})^2} \\
= \sigma(x)(1-\sigma(x))
\end{aligned}
$$

$$
\frac{\partial \bf w^T x_i}{\partial w_i}= \begin{bmatrix} \frac{\partial w_0x_0}{\partial w_i} & \frac{\partial w_1x_1}{\partial w_i} & \frac{\partial w_2x_2}{\partial w_i} &\cdots \frac{\partial w_ix_i}{\partial w_i} & \cdots & \frac{\partial w_nx_n}{\partial w_i}\end{bmatrix}=x_i
$$

　上記より、

$$
\begin{aligned}
\frac{\partial J}{\partial w}
=\frac{\partial J}{\partial y}\frac{\partial y}{\partial w} \\
= - \frac{1}{N} \sum_{i=1}^N \left[ t_i \frac{1}{y_i} - (1-t_i) \frac{1}{1-y_i} \right] \frac{\partial y_i}{\partial w} \\
= - \frac{1}{N} \sum_{i=1}^N \left[ t_i \frac{1}{y_i} - (1-t_i) \frac{1}{1-y_i} \right] y_i (1-y_i) x_i \\
= - \frac{1}{N} \sum_{i=1}^N \left( t_i - y_i \right) x_i
\end{aligned}
$$

４．モデルの実装：スクラッチ編

　動作を理解するためにPythonのライブラリを使用せずスクラッチで計算します。目視で確認できるようにデータ数を1桁に調整しました。

[IN]
class HorizontalDisplay:
    def __init__(self, *args):
        self.args = args
        
    def _repr_html_(self):
        template = '<div style="float: left; padding: 10px;">{}</div>'
        return "\n".join(template.format(a._repr_html_()) for a in self.args)

#データ数が少ないデータセットを作成
df_binary = df[df['label']!=2] #virginicaを除外

#乱数値を生成
np.random.seed(0) #乱数の種を設定
nums_index_binary = np.random.permutation(len(df_binary)) #0~データ数までの整数の乱数生成
nums_index_multi = np.random.permutation(len(df)) #0~データ数までの整数の乱数生成

#パターン1：1次元, 2値分類
df_1dim_binary = df_binary.iloc[nums_index_binary[:8], [0,4]] #sepal length (cm)とlabelのみを抽出
#パターン2：1次元, 3値分類
df_1dim_multi = df.iloc[nums_index_multi[:12], [0,4]] #sepal length (cm)とlabelのみを抽出
#パターン3：2次元, 2値分類
df_2dim_binary = df_binary.iloc[nums_index_binary[:8], [0,1,4]] #sepal length (cm)とsepal width (cm)とlabelのみを抽出
#パターン4：2次元, 3値分類
df_2dim_multi = df.iloc[nums_index_multi[:12], [0,1,4]] #sepal length (cm)とsepal width (cm)とlabelのみを抽出
display(HorizontalDisplay(df_1dim_binary, df_1dim_multi))
display(HorizontalDisplay(df_2dim_binary, df_2dim_multi))


#Excelファイルに出力
# dftoexcel = pd.concat([df_1dim_binary.reset_index(drop=True), df_1dim_multi.reset_index(drop=True), df_2dim_binary.reset_index(drop=True), df_2dim_multi.reset_index(drop=True)], axis=1)
# dftoexcel.to_excel('output/iris_dataset.xlsx')

[OUT]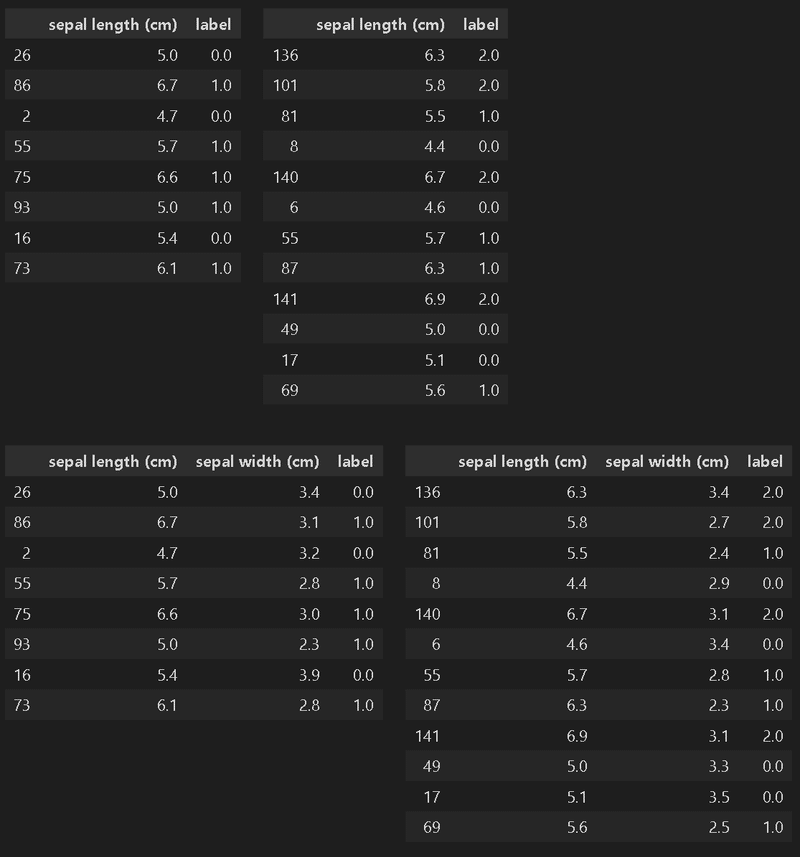

４－１．Pythonで計算：Numpy

　Numpyでロジスティック回帰を実装しましたが２値分類専用となります。手順は下記の通りです。

1. 重みとバイアスを初期化（乱数値作成）

2. 内積で線形予測子を計算

3. シグモイド関数で線形予測子を確率に変換

4. 損失（交差エントロピー）の微分に学習率をかけたものを重み・バイアスに引いてパラメーターを更新

[IN]
#Numpyでロジスティック回帰をスクラッチ実装

class LogisticScratch:
    def __init__(self, lr=0.01, iters=1000, random_state=1):
        self.lr = lr 
        self.iters = iters
        self.random_state = random_state

    def sigmoid(self, x): 
        return 1 / (1 + np.exp(-x)) #シグモイド関数
        
    def fit(self, X, y):
        rgen = np.random.RandomState(self.random_state) #乱数の初期化
        self.w_ = rgen.randn(X.shape[1])/1e5 #重みの初期化
        self.bias_ = rgen.randn(1)/1e5 #バイアスの初期化
        self.cost_ = [] #損失関数の誤差を格納するリスト
        
        for i in range(self.iters):
            input = np.dot(X, self.w_) + self.bias_ #入力値：重回帰モデルと同じ
            output = self.sigmoid(input) #活性化関数：シグモイド関数
            error = (y - output) #誤差：(正解データ-予測値)
            self.w_ = self.w_ + self.lr * np.dot(X.T, error) #重みの更新
            self.bias_ = self.bias_ + self.lr * np.sum(error) #バイアスの更新
            loss = -np.dot(y, np.log(output)) - np.dot((1-y), np.log(1-output)) #損失関数：交差エントロピー誤差
            self.cost_.append(loss) #損失関数の誤差を格納  
        return self
    
    def predict(self, X):
        return np.where(np.dot(X, self.w_) + self.bias_ > 0.5, 1, 0) #予測値：0.5以上なら1, そうでなければ0


#データセット1：1次元, 2値分類
print(f'{"#"*10} データセット1：1次元, 2値分類 {"#"*10}')
x = df_1dim_binary['sepal length (cm)'].values
x = x.reshape(-1, 1) #2次元配列に変換
y = df_1dim_binary['label'].values
print(f'x.shape：{x.shape}, y.shape：{y.shape}\n')

logistic = LogisticScratch(lr=0.05, iters=1000, random_state=1)
logistic.fit(x, y)
y_pred = logistic.predict(x)
df = pd.DataFrame({'y': y, 'y_pred': y_pred})
display(df.T)
print(f'正解率：{np.sum(y_pred==y)/len(y)}, weight：{logistic.w_}, bias：{logistic.bias_}\n')

#データセット2：1次元, 3値分類
print(f'{"#"*10} データセット2：1次元, 3値分類 {"#"*10}')
x = df_1dim_multi['sepal length (cm)'].values
x = x.reshape(-1, 1) #2次元配列に変換
y = df_1dim_multi['label'].values
print(f'x.shape：{x.shape}, y.shape：{y.shape}\n')

logistic = LogisticScratch(lr=0.05, iters=1000, random_state=1)
logistic.fit(x, y)
y_pred = logistic.predict(x)
df = pd.DataFrame({'y': y, 'y_pred': y_pred})
display(df.T)
print(f'正解率：{np.sum(y_pred==y)/len(y)}, weight：{logistic.w_}, bias：{logistic.bias_}\n')

#データセット3：2次元, 2値分類
print(f'{"#"*10} データセット3：2次元, 2値分類 {"#"*10}')
x = df_2dim_binary.iloc[:, :-1].values
y = df_2dim_binary.iloc[:, -1].values
print(f'x.shape：{x.shape}, y.shape：{y.shape}\n')

logistic = LogisticScratch(lr=0.05, iters=1000, random_state=1)
logistic.fit(x, y)
y_pred = logistic.predict(x)
df = pd.DataFrame({'y': y, 'y_pred': y_pred})
display(df.T)
print(f'正解率：{np.sum(y_pred==y)/len(y)}, weight：{logistic.w_}, bias：{logistic.bias_}\n')

#データセット4：2次元, 3値分類
print(f'{"#"*10} データセット4：2次元, 3値分類 {"#"*10}')
x = df_2dim_multi.iloc[:, :-1].values
y = df_2dim_multi.iloc[:, -1].values
print(f'x.shape：{x.shape}, y.shape：{y.shape}\n')

logistic = LogisticScratch(lr=0.05, iters=1000, random_state=1)
logistic.fit(x, y)
y_pred = logistic.predict(x)
df = pd.DataFrame({'y': y, 'y_pred': y_pred})
display(df.T)
print(f'正解率：{np.sum(y_pred==y)/len(y)}, weight：{logistic.w_}, bias：{logistic.bias_}\n')

[OUT]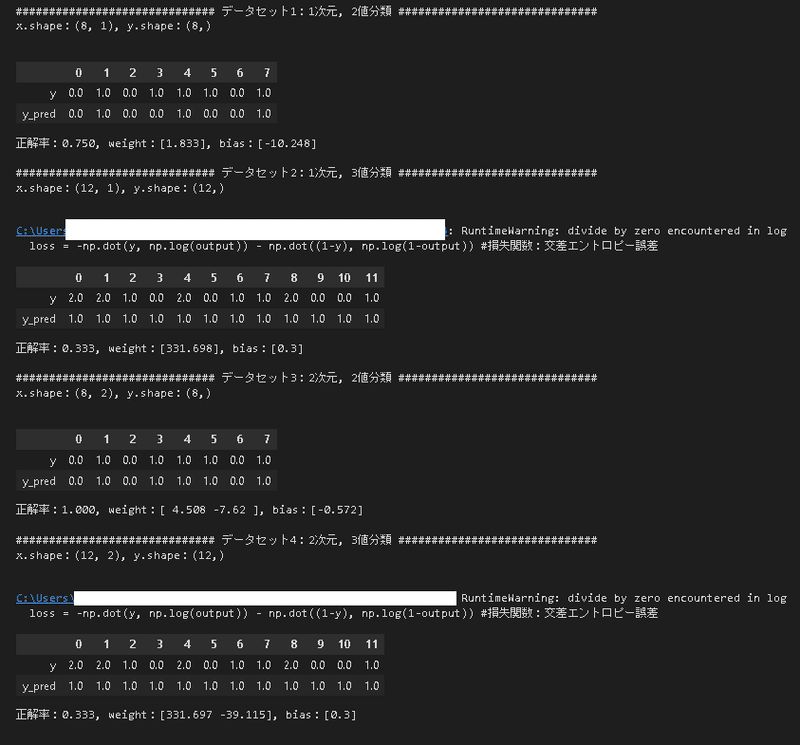

４－２．Excelで計算１：フルスクラッチ

　Excelで計算は可能ではありますが２次元以上のデータでは解が収束しなかったため工夫が必要だと思います（計算違いか初期値が悪いかソルバーが悪いかは不明）。

1. （重回帰と同様の形で）線形予測子を計算

2. シグモイド関数で確率に変換

3. 対数尤度関数を計算

4. 対数尤度関数の合計を計算

5. ソルバーで「対数尤度関数の合計」を最大化

　下記の通り１次元のデータでは計算結果は得られ精度はSklearnと同じでしたがパラメータの値は異なります。また説明変数が２次元の場合は初期値を調整してもうまく収束できませんでした。

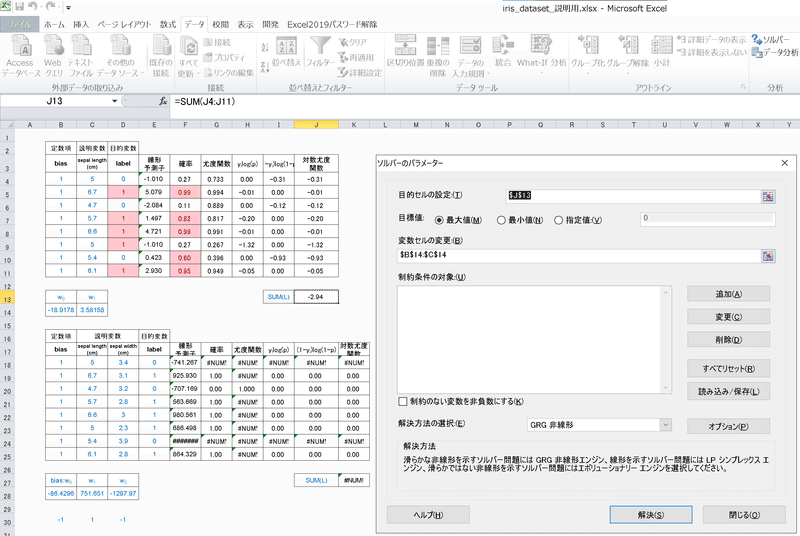
５．単回帰モデルの実装：ライブラリ編

　より簡単にモデルを作成するためにライブラリを使用します。

５－１．Scikit-learn：LinearRegression

　Scikit-learnを使用して重回帰を実装します。こちらは単回帰と同じく、重回帰は”LinearRegression”で実装できます。
　Scikit-learnのAPIはシンプルでありモデルは下記フローで実装できます。

1. 使用する機械学習モデルをインポート

2. モデルのインスタンス化

3. 学習：model.fit()

4. 学習後のパイパーパラメータ確認

5. 推論：model.predict()

[IN]
np.set_printoptions(precision=3, suppress=True) #小数点以下3桁, 指数表記を抑制
from sklearn.linear_model import LogisticRegression

#データセット1：1次元, 2値分類
print(f'{"#"*10} データセット1：1次元, 2値分類 {"#"*10}')
X, y = df_1dim_binary.iloc[:, :-1], df_1dim_binary.iloc[:, -1] #データとラベルを取得
logistic = LogisticRegression() #インスタンスを生成
logistic.fit(X, y) #モデルを学習
y_pred = logistic.predict(X) #予測
df = pd.DataFrame({'y': y, 'y_pred': y_pred}) #データフレームに変換
display(df.T)
print(f'正解率：{logistic.score(X, y):.2f}, weight：{logistic.coef_}, bias：{logistic.intercept_}\n')

#データセット2：1次元, 3値分類
print(f'{"#"*10} データセット2：1次元, 3値分類 {"#"*10}')
X, y = df_1dim_multi.iloc[:, :-1], df_1dim_multi.iloc[:, -1] #データとラベルを取得
logistic = LogisticRegression() #インスタンスを生成
logistic.fit(X, y) #モデルを学習
y_pred = logistic.predict(X) #予測
df = pd.DataFrame({'y': y, 'y_pred': y_pred}) #データフレームに変換
display(df.T)
print(f'正解率：{logistic.score(X, y):.2f}, weight：{logistic.coef_.reshape(1,-1)}, bias：{logistic.intercept_}\n')

#データセット3：2次元, 2値分類
print(f'{"#"*10} データセット3：2次元, 2値分類 {"#"*10}')
X, y = df_2dim_binary.iloc[:, :-1], df_2dim_binary.iloc[:, -1] #データとラベルを取得
logistic = LogisticRegression() #インスタンスを生成
logistic.fit(X, y) #モデルを学習
y_pred = logistic.predict(X) #予測
df = pd.DataFrame({'y': y, 'y_pred': y_pred}) #データフレームに変換
display(df.T)
print(f'正解率：{logistic.score(X, y):.2f}, weight：{logistic.coef_.reshape(1,-1)}, bias：{logistic.intercept_}\n')

#データセット4：2次元, 3値分類
print(f'{"#"*10} データセット4：2次元, 3値分類 {"#"*10}')
X, y = df_2dim_multi.iloc[:, :-1], df_2dim_multi.iloc[:, -1] #データとラベルを取得
logistic = LogisticRegression() #インスタンスを生成
logistic.fit(X, y) #モデルを学習
y_pred = logistic.predict(X) #予測
df = pd.DataFrame({'y': y, 'y_pred': y_pred}) #データフレームに変換
display(df.T)
print(f'正解率：{logistic.score(X, y):.2f}, weight：{logistic.coef_.reshape(1,-1)}, bias：{logistic.intercept_}\n')

[OUT]

　可視化に関しては省略します。

[IN]
[OUT]

【コラム】
　３次元空間(x,y,z)に対して2次元（平面）で表現される空間、つまり元の空間(n次元)より1次元低い空間(n-1次元)を超平面と呼びます。
　重回帰では独立変数（説明変数）が２つの場合は”回帰平面”、３つ以上では”回帰超平面”と呼びます。

５－２．Pytorch：nn.Linear()

　Pytorchで重回帰も実装できますが、sklearnの方が楽のため省略します。

６．補足：関数の紹介

６－１．シグモイド関数

　MIN=0, MAX=1かつx=0でy=0.5の値をとるため、「入力値を確率に変換」する関数として用いられます。
　深層学習では活性化関数として使用されていましたが、微分の最大値が0.25のため誤差逆伝搬時に勾配消失が生じるため現在では使用されていません。

$$
\sigma(x)=\frac{1}{1+\exp(-x)}
$$

$$
\frac{df(x)}{dx}=\sigma(x)(1-\sigma(x))
$$

[IN]
import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def diff_sigmoid(x):
    return (1.0 - sigmoid(x)) * sigmoid(x)

x = np.arange(-5.0, 5.0, 0.1)
fig, ax = plt.subplots(1, 1, figsize=(8, 5))
ax.plot(x, sigmoid(x), label='sigmoid')
ax.plot(x, diff_sigmoid(x), label='\u0394sigmoid')
ax.set(xlabel='x', ylabel='y', title='Sigmoid function',
       xlim=(-5, 5), ylim=(0.0, 1.0), xticks=np.arange(-5, 6, 1), yticks=np.arange(0, 1.1, 0.1))
ax.grid(), ax.legend()
plt.show()

[OUT]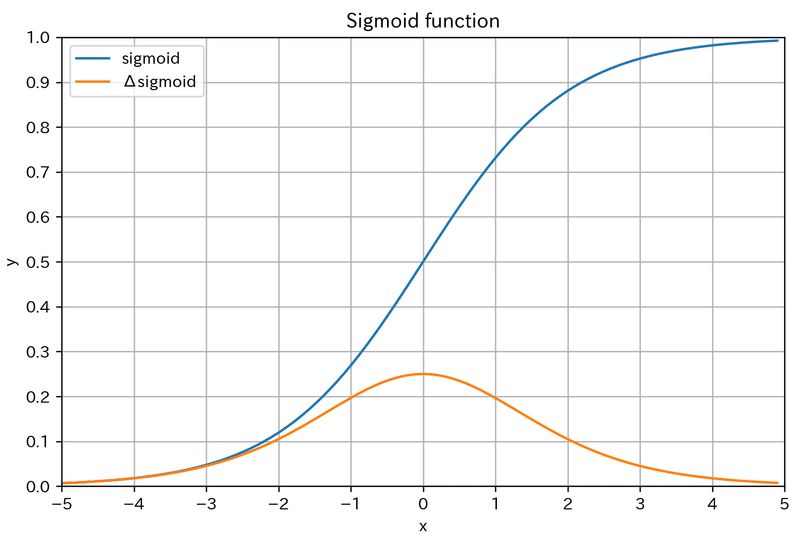

【参考：シグモイド関数の微分の導出】

$$
\begin{aligned}
\frac{d}{dx}\sigma(x)
&= \frac{d}{dx}\left(\frac{1}{1+\exp(-x)}\right)\\
&= \frac{\frac{d}{dx}(1)\cdot(1+\exp(-x))-1\cdot\frac{d}{dx}(1+\exp(-x))}{(1+\exp(-x))^2} \\
&= \frac{\exp(-x)}{(1+\exp(-x))^2}\\
&= \frac{1}{1+\exp(-x)} \cdot \frac{\exp(-x)}{1+\exp(-x)}\\
&= \sigma(x) \cdot \frac{\exp(-x)}{1+\exp(-x)}\\
&= \sigma(x) \cdot \frac{\exp(-x)+1-1}{1+\exp(-x)}\\
&= \sigma(x) \cdot \left(\frac{\exp(-x)+1}{1+\exp(-x)}-\frac{1}{1+\exp(-x)}\right)\\
&= \sigma(x) \cdot \left(1-\frac{1}{1+\exp(-x)}\right)\\
&= \sigma(x) (1-\sigma(x))
\end{aligned}
$$

６－２．（標準）ロジスティック関数

　次節で述べるロジット関数$${y=\log\dfrac{p}{1-p}}$$の逆関数です。複数の係数を持ち多様な形状を設定できます。
　特定の値における関数を「標準ロジスティック関数」と呼び、シグモイド関数と同じになります。つまりシグモイド関数の拡張版のような関数です。

$$
g(x)=\dfrac{A}{1+e^{-k(x-x_0)}}
$$

$$
標準ロジスティック関数g(x)=\dfrac{1}{1+e^{-x}}
$$

[IN]
#ロジスティック関数
def logisticfunc(x:float, a:float, b:float, c:float):
    return a / (1 + np.exp(-b * (x - c)))

x = np.linspace(-5, 5, 100)
y1 = logisticfunc(x, 1, 1, 0) #a=1, b=1, c=0: シグモイド関数と同じ
y2= logisticfunc(x, 1, 1, 3) #a=1, b=1, c=3: シグモイド関数より右にずらした
y3 = logisticfunc(x, 2, 1, 0) #a=2, b=1, c=0: シグモイド関数より上にずらした
y4 = logisticfunc(x, 1, 3, 0) #a=1, b=3, c=0: シグモイド関数より上にずらした

fig, ax = plt.subplots(figsize=(8, 6), facecolor='white')
ax.plot(x, y1, label='a=1, b=1, c=0: Sigmoid')
ax.plot(x, y2, label='a=1, b=1, c=3')
ax.plot(x, y3, label='a=3, b=1, c=0')
ax.plot(x, y4, label='a=1, b=3, c=0')
ax.plot((0, 0), (0, 10), color='black', lw=1), ax.plot((-5, 5), (0, 0), color='black', lw=1) #x軸, y軸
ax.set(xlabel='x', ylabel='y', title='ロジスティック関数', xticks=np.arange(-5, 6, 1), yticks=np.arange(0, 2, 0.2), ylim=(0, 2))
ax.grid(), ax.legend()
plt.show()

[OUT]

　結果より、係数を調整することで最大値(最小値は0のまま）、カーブの傾斜、$${\frac{Max}{2}}$$の位置を調整できることが確認できます。

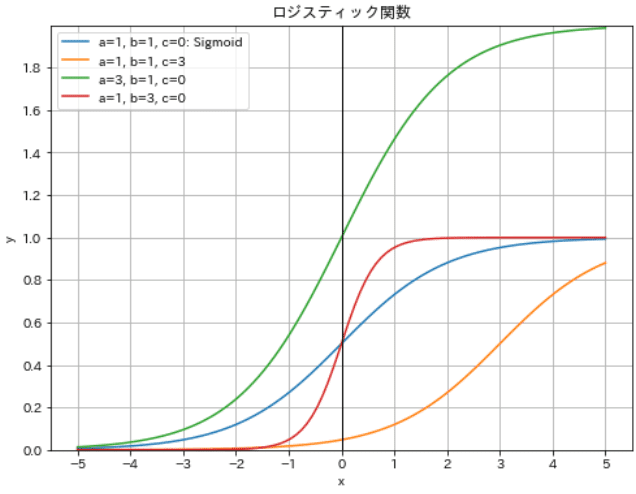
６－３．ロジット関数

事象Aが生じる確率：$${p}$$、Aの余事象（Aが生じない確率）：$${1-p}$$としたときの確率の比：オッズであり、オッズの対数がロジット関数$${\log(\frac{p}{1-p})}$$です。
　ロジスティック回帰では、このロジット関数を次節で紹介するリンク関数として使用します。

• 確率pの定義域は 0<p<1

• p→0で f(p)→−∞、p→1で f(p)→∞

• p=0と p=1が漸近線

• $${p=\dfrac{1}{2}}$$で f(p)=0です。$${(\frac{1}{2},0)}$$に関して点対称

• ロジスティック関数（シグモイド関数）の逆関数（入力値$${x}$$があり、関数$${f(x)}$$の出力値を元に戻す関数$${g(f(x))=x}$$)

$$
f(p)=\log(\frac{p}{1-p})  =\log p-\log(1-p)
$$

[IN]
def logit_func(x):
    return np.log(x / (1 - x))

x = np.arange(0.01, 1.0, 0.01)
fig, ax = plt.subplots(1, 1, figsize=(8, 5), facecolor='w')
ax.plot(x, logit_func(x), label='logit')
ax.plot((0, 1), (0, 0), color='black', lw=1), ax.plot((0, 0), (-5, 5), color='black', lw=1) #x軸とy軸
ax.set(xlabel='x', ylabel='y', title='Logit function', xticks=np.arange(0, 1.1, 0.1), yticks=np.arange(-5, 6, 1))
ax.grid(), ax.legend()
plt.show()

[OUT]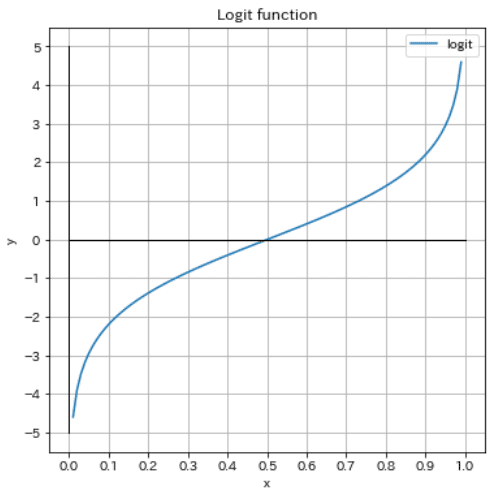

【オッズ】
　オッズ$${\frac{p}{1-p}}$$を図式化しました。下図より確率pが増加すると急激にオッズが増加している->より高い比率で生じやすいことが分かります。
　なお競馬のオッズは計算方式が異なるためご注意ください。

[IN]
#オッズ
p = np.arange(0, 0.95, 0.01) #確率
p_inv = 1 - p
odds = p / p_inv #オッズ

#グラフ化
fig, ax = plt.subplots(1, 1, figsize=(6, 6), facecolor='w')
ax.plot(p, odds, label='odds')
ax.set(xlabel='確率p', ylabel='odds', title='Odds function', xticks=np.arange(0, 1.1, 0.1), yticks=np.arange(0, 16.1, 1))
ax.grid(), ax.legend()
plt.show()

[OUT]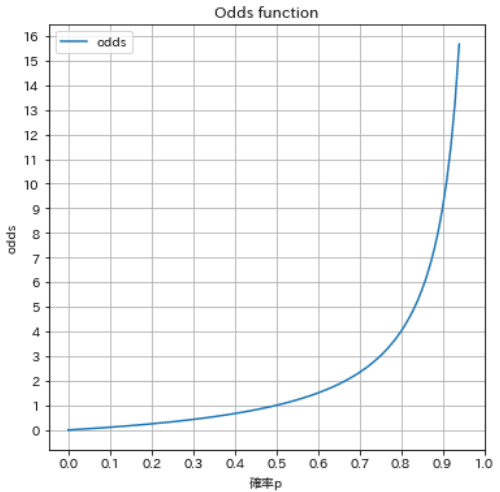

【ロジット関数の逆関数の証明】
　ロジット関数の逆関数がシグモイド関数になることを確認します。この仕組みよりシグモイド関数は”標準ロジスティック関数：Standard logistic function”とも呼ばれます。

$$
\begin{aligned}
x=\log\dfrac{p}{1-p} \\
e^x=\dfrac{p}{1-p} \\
e^x-e^xp=p \\
p=\dfrac{e^x}{e^x+1}=\dfrac{1}{1+e^{-x}}
\end{aligned}
$$

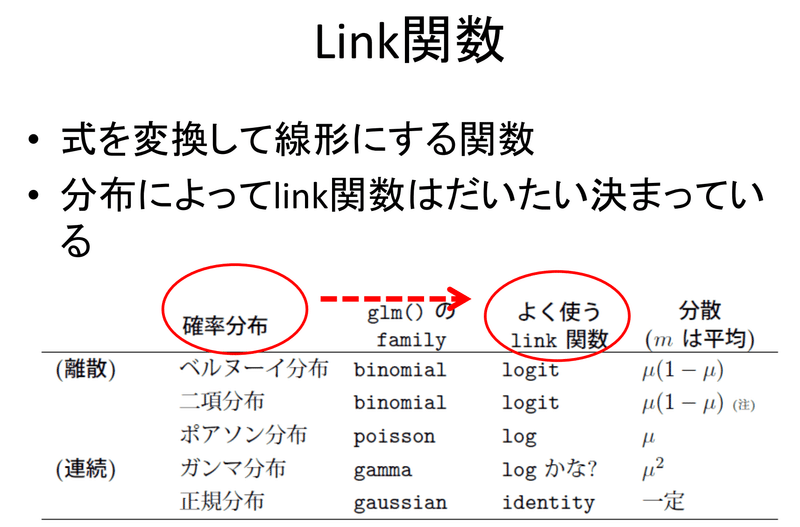
６－４．リンク関数

　リンク関数とは「カテゴリ応答変数の各水準の確率を、限界のない連続スケールに変換する関数」？？です。おそらく「”離散値”と”連続値”」や「”確率(0~1)”と”実数（-∞~∞）”」のように同等と扱えない値同士をつなぐための関数だと理解しています。
　コイントスの例では確率->実数（-∞~∞）の連続値へ変換しています。これの逆関数を使用すれば実数（-∞~∞）->確率への変換可能です。

[IN]
class CoinToss:
    def __init__(self, nums_play: int, nums_toss: int, p: float):
        self.nums_play = nums_play #試行回数(サンプル数)
        self.nums_toss = nums_toss #コイントス回数(サンプルサイズ)
        self.p = p #表の確率
        self.values = np.array([0, 1]) #0: 裏, 1: 表
        
    def __call__(self):
        outputs = [] #全結果
        for _ in range(self.nums_play):
            # n回目のコイントス(試行)
            counts = np.random.choice(self.values, self.nums_toss, p=[1 - self.p, self.p]) #play
            counts_head = np.sum(counts) #表の回数
            outputs.append([counts, counts_head])
        return outputs
    
#コイントス
np.random.seed(12) #乱数の固定
nums_play, nums_toss, p = 100, 10, 0.7 #プレイ数：50, コイントス回数：10, 表の確率：0.7
cointoss = CoinToss(nums_play, nums_toss, p)
outputs = cointoss() #出力：試行結果, 表の回数
heads = [output[1] for output in outputs] #表の回数のみ

#表の回数を集計
counts_head = np.bincount(heads, minlength=11) #表が出た回数
props_head = counts_head / np.sum(counts_head) #表が出た確率

#リンク関数（ロジット関数）による確率変換
def logit(p):
    return np.log(p / (1 - p)) #ロジット関数

logit_probs = logit(props_head[1:]) #ロジット関数による確率変換

#グラフ化
X = np.arange(1, nums_toss+1, 1) #x軸: 表の回数
print(f'形状確認：X={X.shape}, props_head={props_head.shape}, logit_probs={logit_probs.shape}')

fig, axs = plt.subplots(2, 2, figsize=(12,12), facecolor='w')
axs = axs.ravel() #2次元配列を1次元配列に変換
axs[0].bar(X, props_head[1:], align='center', width=0.5, label='counts')
axs[0].set(xlabel=f'コイントス回数{nums_toss}：表の回数', ylabel='表の出現確率:p', title=f'コイントス試行(試行数:{nums_play}, p={p})', xticks=np.arange(1, 11, 1), yticks=np.arange(0, 1.1, 0.1))
[axs[0].text(x-0.5, y+0.02, f'p={y:.2f}', fontsize=8) for x, y in zip(X, props_head[1:])] #確率の表示
axs[0].grid(), axs[0].legend()

axs[1].plot(np.linspace(0, 1, 100), logit(np.linspace(0, 1, 100)), label='logit')
axs[1].set(xlabel='確率p', ylabel='log(p/(1-p))', title='ロジット関数', xticks=np.arange(0, 1.1, 0.1), yticks=np.arange(-5, 6, 1))
axs[1].grid(), axs[1].legend()

axs[2].plot(X, logit_probs, label='logit')
axs[2].set(xlabel=f'コイントス回数{nums_toss}：表の回数', ylabel='log(p/(1-p))', title='リンク関数(ロジット関数)による確率変換:回数 vs logit', xticks=np.arange(1, 11, 1), yticks=np.arange(-5, 6, 1))
axs[2].grid(), axs[2].legend()

axs[3].scatter(props_head[1:], logit_probs, label='logit')
axs[3].set(xlabel='表の出現確率:p', ylabel='log(p/(1-p))', title='リンク関数(ロジット関数)による確率変換:p vs logit', xticks=np.arange(0, 1.1, 0.1), yticks=np.arange(-5, 6, 1))
axs[3].grid(), axs[3].legend()

fig.savefig('output/link関数の理解.png')

[OUT]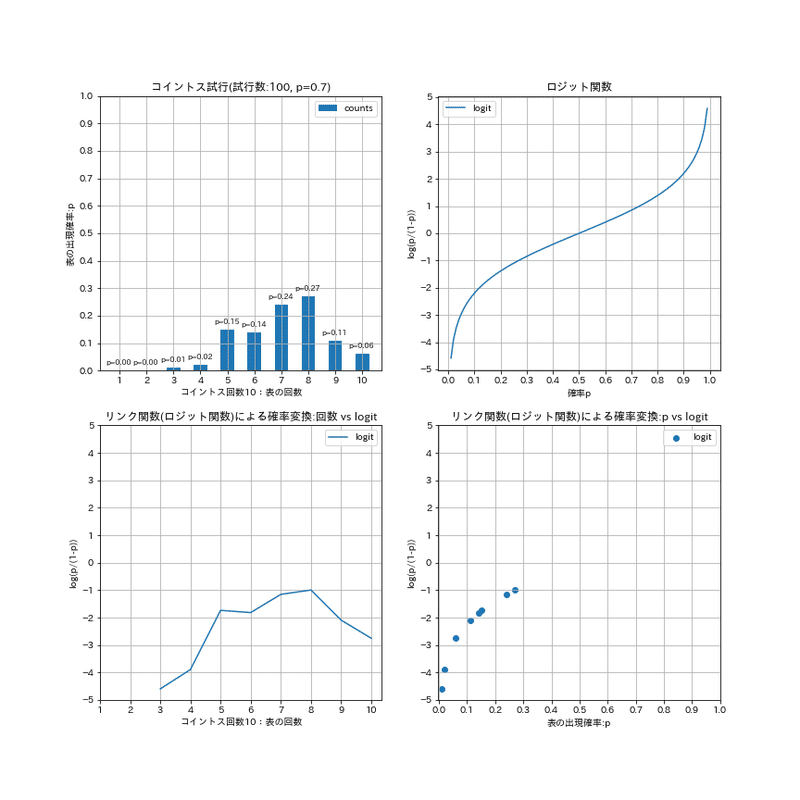

６－５．尤度関数／最尤推定

尤度/尤度関数（likelihood）とは「母数 θ の各値のもとで，その値がどの程度起りやすいか（確率）をθ の関数として考えたもの」です。
　最尤推定とは尤度関数を最大化することによっても出るパラメータの最適な値を求める手法です。

https://www.ritsumei.ac.jp/~ttt20009/classes/0809/binary.pdf

http://www3.u-toyama.ac.jp/kkarato/2020/statistics/handout/Statistics[A]-2020-11-0605.pdf

６－６．交差エントロピー誤差(cross entropy error)

　公差エントロピー誤差とは分類問題でよく使用される目的関数（誤差関数）です。

【多クラス分類】
モデルの出力値(※確率0~1)：$${y_k}$$、正解値：$${t_k}$$とすると下記の通りです。

$$
E = – \sum_{k=1}^N t_k \log y_k
$$

【２値分類：Binary Cross-Entropy(BCE)】
２値分類においてモデルの出力値$${p}$$（シグモイド関数を通した後の確率0~1)、正解値(2値：0, 1)$${y}$$としたときの交差エントロピーは下記の通りです。

$$
\displaystyle E=\sum_{k=1}-{(y\log(p) + (1 - y)\log(1 - p))}
$$

６－７．ソフトマックス関数 (softmax function)

　多分類などにおいて、実数での値を確率に変換する関数です。よってシグモイド関数の多値Ver.のようなものになります。

$$
softmax(x)=\frac{e^{x_i}}{\sum _{i=1}^n e^{x_i}}
$$

　参考例は下記の通りです。

$$
\begin{aligned}
X=\begin{bmatrix} 1 \\ 4 \\ 2 \\ 5 \\ 8 \end{bmatrix}
\end{aligned}
$$

$$
\begin{aligned}
\sum_{i=1}^n e^x=exp(1)+exp(4)+exp(2)+exp(5)+exp(8)= 2.72 + 54.6 + 7.39 + 148.4 + 2981 = 3194.1
\end{aligned}
$$

$$
\begin{aligned}
y=\frac{1}{\sum_{i=1}^n e^x}\begin{bmatrix} 1 \\ 4 \\ 2 \\ 5 \\ 8 \end{bmatrix}
=\frac{1}{3194.1}\begin{bmatrix} 1 \\ 4 \\ 2 \\ 5 \\ 8 \end{bmatrix}
=\begin{bmatrix}0.001 \\ 0.017 \\ 0.002 \\ 0.046 \\ 0.933 \end{bmatrix}
\end{aligned}
$$

　なお上記をそのまま実装するとオーバフローとなる可能性があるため、配列の最大値を分子・分母の入力値に足して計算します。なお数式上、このような変換をしても結果は同じとなります。

[IN]
def softmax(x):
    c = np.max(x)
    exp_x = np.exp(x - c)
    sum_exp_x = np.sum(exp_x)
    y = exp_x / sum_exp_x
    return y

[OUT]

$$
\\ f(x_i) = \frac{e^{x_i}}{\sum _{k=1}^n e^{x_k}} \\ \qquad = \frac{C e^{x_i}}{C \sum _{k=1}^n e^{x_k}} \\ \qquad = \frac{e^{x_i + \log C}}{\sum _{k=1}^n (e^{x_k} + \log C)} \\ \qquad = \frac{e^{x_i + C’}}{\sum _{k=1}^n (e^{x_k} + C’)} \\
$$

７．補足２：ベクトル・行列式の変換

【ベクトルの内積の入れ替え：$${{\bf w}^{\rm T}{\bf x}= {\bf x}^{\rm T}{\bf w}}$$】

$$
\begin{aligned}
{\bf w}^{\rm T}{\bf x}= {\bf x}^{\rm T}{\bf w}
= w_{0}x_{0} + w_{1}x_{1} + \cdots + w_{N}x_{N}
= \begin{bmatrix} w_{0} \ w_{1}\ w_{2} \ \dots \ w_{n} \end{bmatrix}
\begin{bmatrix} x_{0} \\ x_{1}\\ x_{2} \\ \vdots \\ x_{n} \end{bmatrix}
=\begin{bmatrix} x_{0} \ x_{1}\ x_{2} \ \dots \ x_{n} \end{bmatrix}
\begin{bmatrix} w_{0} \\ w_{1}\\ w_{2} \\ \vdots \\ w_{n} \end{bmatrix}
\end{aligned}
$$

【転置の公式】

$$
\begin{aligned} &\ \left( {\bf A}^{\rm T} \right)^{\rm T} = {\bf A} \\
& \ \left( {\bf A}{\bf B} \right)^{\rm T} = {\bf B}^{\rm T}{\bf A}^{\rm T}\\
&\ \left( {\bf A}{\bf B}{\bf C} \right)^{\rm T} = {\bf C}^{\rm T}{\bf B}^{\rm T}{\bf A}^{\rm T} \end{aligned}
$$

$$
\begin{aligned}
{\bf A} \in \mathbb{R}^{N \times M }&
= \begin{bmatrix} a_{10} & a_{11} & a_{12} & \cdots & a_{1M} \\ a_{20} & a_{21} & a_{22} & \cdots & a_{2M} \\a_{30} & a_{31} & a_{32} & \cdots & a_{3M} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{N0} & a_{N1} & a_{N2} & \cdots & a_{NM} \end{bmatrix},
{\bf B} &\in \mathbb{R}^{M \times O }
= \begin{bmatrix} b_{10} & b_{11} & b_{12} & \cdots & b_{1O} \\ b_{20} & b_{21} & b_{22} & \cdots & b_{2O} \\b_{30} & b_{31} & b_{32} & \cdots & b_{3O} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ b_{M0} & b_{M1} & b_{M2} & \cdots & b_{MO} \end{bmatrix}
\end{aligned}
$$

$$
\begin{aligned}
{\bf A}^{\rm T} \in \mathbb{R}^{M \times N }&
= \begin{bmatrix} a_{10} & a_{20} & a_{30} & \cdots & a_{N0} \\
a_{11} & a_{21} & a_{31} & \cdots & a_{N1} \\
a_{12} & a_{22} & a_{32} & \cdots & a_{N2} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
a_{1M} & a_{2M} & a_{3M} & \cdots & a_{NM} \end{bmatrix}
,
{\bf B}^{\rm T} \in \mathbb{R}^{O \times M }
= \begin{bmatrix} b_{10} & b_{20} & b_{30} & \cdots & b_{M0} \\
b_{11} & b_{21} & b_{31} & \cdots & b_{M1} \\
b_{12} & b_{22} & b_{32} & \cdots & b_{M2} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
b_{1O} & b_{2O} & b_{3O} & \cdots & b_{MO} \end{bmatrix}
\end{aligned}
$$

$$
\begin{aligned}
{\bf B}^{\rm T} {\bf A}^{\rm T} =
\begin{bmatrix} b_{10} & b_{20} & b_{30} & \cdots & b_{M0} \\
b_{11} & b_{21} & b_{31} & \cdots & b_{M1} \\
b_{12} & b_{22} & b_{32} & \cdots & b_{M2} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
b_{1O} & b_{2O} & b_{3O} &\cdots & b_{MO}  \end{bmatrix}
\begin{bmatrix} a_{10} & a_{20} & a_{30} & \cdots & a_{N0} \\
a_{11} & a_{21} & a_{31} & \cdots & a_{N1} \\
a_{12} & a_{22} & a_{32} & \cdots & a_{N2} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
a_{1M} & a_{2M} & a_{3M} & \cdots & a_{NM}
\end{bmatrix}
\end{aligned}
$$

【ベクトルの微分１：$${\frac{\partial}{\partial {\bf x}} \left( {\bf w}^{\rm T}{\bf x} \right) = {\bf w}^{\rm T}}$$】

$$
\begin{aligned}
\frac{\partial}{\partial {\bf x}} \left( {\bf w}^{\rm T}{\bf x} \right)
=\frac{\partial}{\partial {\bf x}}(w_{0}x_{0} + w_{1}x_{1} + \cdots + w_{N}x_{N})
=\frac{\partial}{\partial {\bf x}}\sum_{i=1}^{n}w_ix_i
\end{aligned}
$$

$$
\begin{aligned}
=\begin{bmatrix}
\frac{\partial}{\partial x_1} \left(\sum_{i=1}^{n}w_ix_i \right) &
\frac{\partial}{\partial x_2} \left(\sum_{i=1}^{n}w_ix_i \right) & \dots &
\frac{\partial}{\partial x_n} \left(\sum_{i=1}^{n}w_ix_i \right)
\end{bmatrix}
= \begin{bmatrix} w_{0} \ w_{1}\ w_{2} \ \dots \ w_{n} \end{bmatrix}
= {\bf w}^{\rm T}
\end{aligned}
$$

【ベクトルの微分２：$${\frac{\partial}{\partial {\bf x}} \left( {\bf x}^{\rm T}{\bf A}{\bf x} \right) = {\bf x}^{\rm T} \left( {\bf A} + {\bf A}^{\rm T} \right)}$$】

$$
\begin{aligned}
{\bf x}^{\rm T}{\bf A}{\bf x}
&= \begin{bmatrix} x_1 & x_2 & \cdots & x_N \end{bmatrix}
\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1N} \\
a_{21} & a_{22} & \cdots & a_{2N} \\
\vdots & \vdots & \ddots & \vdots \\
a_{N1} & a_{N2} & \cdots & a_{NN} \end{bmatrix}
\begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_N \end{bmatrix}
=\begin{bmatrix} \sum_{i=1}^{N}x_ia_{i1} & \sum_{i=1}^{N}x_ia_{i2} & \cdots & \sum_{i=1}^{N}x_ia_{iN} \end{bmatrix}
\begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_N \end{bmatrix}
= \sum_{i=1}^{N} \sum_{j=1}^{N} a_{ij} x_i x_j
\end{aligned}
$$

$$
\begin{aligned}
\frac{\partial}{\partial {\bf x}} \left( {\bf x}^{\rm T}{\bf A}{\bf x} \right)
&= \frac{\partial}{\partial {\bf x}} \left( \sum_{i=1}^{N} \sum_{j=1}^{M} a_{ij} x_i x_j \right) \
&= \begin{bmatrix} \frac{\partial}{\partial x_1} & \frac{\partial}{\partial x_2} & \cdots & \frac{\partial}{\partial x_N} \end{bmatrix} \begin{bmatrix} \sum_{i=1}^{N} \sum_{j=1}^{N} a_{ij} x_i x_j \end{bmatrix}
\end{aligned}
$$

$$
\begin{aligned}
= \begin{bmatrix} \sum_{j=1}^{N} a_{1j} x_j & \sum_{j=1}^{N} a_{2j} x_j & \cdots & \sum_{j=1}^{N} a_{Nj} x_j \end{bmatrix}
\end{aligned}
$$

$$
\begin{aligned}
&= \begin{bmatrix} x_1 & x_2 & \cdots & x_N \end{bmatrix}
\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1N} \\
a_{21} & a_{22} & \cdots & a_{2N} \\
\vdots & \vdots & \ddots & \vdots \\
a_{N1} & a_{N2} & \cdots & a_{NN} \end{bmatrix} +
\begin{bmatrix} x_1 & x_2 & \cdots & x_N \end{bmatrix}
\begin{bmatrix} a_{11} & a_{21} & \cdots & a_{N1} \\
a_{12} & a_{22} & \cdots & a_{N2} \\
\vdots & \vdots & \ddots & \vdots \\
a_{1N} & a_{2N} & \cdots & a_{NN}
\end{bmatrix} \
&= {\bf x}^{\rm T} \left( {\bf A} + {\bf A}^{\rm T} \right)
\end{aligned}
$$

参考資料

Pythonコード

モデル理論

https://cogpsy.educ.kyoto-u.ac.jp/personal/Kusumi/datasem13/shrasuna1.pdf

あとがき

　数式部分をChatGPTに補助してもらったけど、最初に理解できてなかったからあとで見返すと記号がまちまちになってる。
　もっと最初の方から明確に記号合わせておかないと、理解が難しくなるので反省。
　後、製作期間２～３週間くらいかかったからなかなかしんどかった＋後で見直しします。