右の道は上り坂？
左の道は下り坂？
ここは一番高い場所。右も左も下り坂。

◎　◎　◎

$${x+y=13}$$
$${4x+2y=34}$$
第一の式から$${y=13-x}$$を導いて、第二の式の代入すると
$${4x+2(13-x)=34}$$
よって$${x=4, y=9}$$

連立一次方程式の基本的な問題だ。ひねりはないけれど、ケチをつけるような問題ではない…はずだが。

リコ「面積図書けばよくない？？」

わがままお嬢様は、いつものように文句を垂れながら、いつものように問題文を無視して図を書いていた。

リコ「 x とか y って何が起きてるのかよくわかんないんだよねー。図を書いちゃえば一撃だよ。一撃！」

そう言いながらこぶしを前に突き出す。「一撃」のジェスチャーなのだろう。

いつもの図書室の一角には、僕とリコの2人。今日はコノミも来ているけれど、「読みたい本がある」といってさっさと2階に上がってしまった。彼女が持っていた本は、トマ・ピケティの『21世紀の資本』だ。「経済学書としては稀に見るベストセラーなの」と嬉しそうに話してくれたことがある。

この図書室には、10万冊の本があるという。1階の一番手前の棚に並んでいるのが新書で、その奥に法律や政治・経済、さらにその奥に数学や自然科学の本がところ狭しと並んでいる。2階には辞典や小説がある。現代日本政治研究同好会が間借りしているスペースの周りには雑誌や児童書があって、ちょっとした休憩スペースのような扱いになっている。

僕はまだ本格的な経済学書を読んだことがないけれど、コノミによるとこの図書館には経済学の基本書がたくさんあって非常に助かるのだという。

マンキュー、ブランシャール、スティグリッツ。

外国の学者が書いた本は読む前から難しく感じてしまう。「入門」なんてついていても、それらは僕よりずっと知識がある人達に向けて書かれたものだ。気が遠くなるほど勉強してもきっとすべてを理解することができないと思うと、ちょっと切ない。

コノミ「この図形の縦の長さの単位は何？」

いつの間にか2階から戻ってきたコノミが、座っているリコの後ろから机に手をかけて話しかけていた。首もとまで伸ばした髪を耳にかけるしぐさが、ふと目に留まる。

リコ「単位？センチメートル？」

コノミ「それは距離の単位。この図形の縦の長さは、足の数を表しているんでしょう？ということは、単位は何？」

リコ「ええー？どういうこと？足の数だから、”本”ってこと？」

2人の少女の会話を見守る。

コノミ「じゃあ、この図形の横の長さの単位は？」

リコ「”匹”！…あれ？鶴は”匹”でいいんだっけ？」

1羽、2羽、と数えるイメージがある。鳥だし。
でも、多分今は日本語クイズをしている訳ではないのだろう。

コノミ「じゃあ、この図形の面積の単位、つまり縦の長さ×横の長さで表される量の単位は？」

リコ「足の数だから”本”！」

話が見えてきたぞ。縦の長さの単位が”本”、横の長さの単位が”匹”だったら、縦の長さ×横の長さで表される面積の単位は”本×匹”になってしまう。

$${2本×9匹=18本匹}$$

”本匹”なんて単位はない。そもそも、この図形の面積は”本”を表している。ということは——。

コノミ「縦の長さと横の長さの積が”本”を表すのよ。で、横の長さの単位は”匹”。ということは、縦の長さの単位は正確に言うと？」

リコ「うーん…？」

僕「”$${本/匹}$$”だよ。”一匹あたり～本”と言ってもいいね」

しまった。つい言葉に出てしまった。今日は2人の会話を眺めていようと思ったのに。
引っ込みがつかなくなった僕は、そのまま式を書く。

$$
2\frac{本}{匹}×9匹=18本
$$

僕「こうやって書くと、分母の”匹”と分子の”匹”を消せるでしょ。だから、$${2×9=18}$$に”本”をつけて、18本という答えを出せる」

コノミ「単位が分数の形になることはよくあるわね。速さの単に”$${m/s}$$”というものがあるけれど、これは1秒あたりに何m進むかを表しているわ」

僕「SecondのSが秒を表しているね」

リコ「あー！それ英語の授業でやったー！」

コノミ「単位が分数の形を取るとき、割り算を表す記号”/”はperと読むことがある。典型的なのは、『100分のいくつに相当するか』を表すパーセントね。セントは100という意味」

ゲーム用語では、1秒間で与えるダメージをダメージパーセカンド（DPS）と言ったり、1秒間のフレーム数をフレームパーセカンド（FPS）と言ったりするけど、これは黙っておこう。

コノミ「自然科学や経済学では、数値化された量の単位を常に意識する必要があるわ。経済学の場合は、一定時間あたりの変化を表すフローと、ある時点までの累積量を表すストックを区別することが重要になる…けど、この話はまた今度しよう」

彼女はそれまでずっと脇に抱えていた『21世紀の資本』を机に置いた。

僕「物理では速さを表す"$${m/s}$$"の他に、1秒あたりの速さの変化、つまり加速度を表す"$${m/s^2}$$"とか、ある質量の物体をどのくらい加速させるか、つまり力を表す"$${kg･m/s^2}$$"とか出てきてややこしいんだよね」

リコ「"$${kg･m/s^2}$$"でひとつの単位なの！？」

僕「1 $${kg･m/s^2}$$を1N(1ニュートン)と書くこともできるね」

コノミ「加速度や力といった複雑な物理量は、質量・長さ（距離）・時間といった基礎的な物理量の掛け算と割り算によって構成されるわ。複雑な物理量を扱うときに、どのような基礎的な物理量の組み合わせによって構成されているかに注目することを、次元解析と呼ぶ。次元が異なるものは足したり引いたりできないし、大小を比較することもできないわね」

物理の授業で習ったことを思い出す。等式の両辺は必ず次元が一致していなければならない――単位が異なるものは、大小を比較したり等号で結んだりできないという話だ。

リコ「今日は物理の話をするの？リコ、物理は大好き！実験が楽しいから！！」

そう言って、もともと大して進める気がなかったであろう数学の問題集をカバンにしまう。

コノミ「いえ、今日は需要関数と次元の話――需要曲線によって囲まれる領域の面積の話をするわ」

リコ「強引！？」

経済学ガールの講義が始まる。

◎　◎　◎

僕たちはホワイトボードの前に移動した。カウンターの横にある壁がホワイトボードになっているのだ。プロジェクターも投影できるから、授業はもちろん部活のミーティングで使われることもあるけど、今日はたまたま空いていた。

コノミがホワイトボードに需要曲線を描く。

コノミ「さて、このグラフは縦軸が価格を、横軸が需要量を表しているのだけれど、面積は何を表していると思う？」

リコ「ちょっと待って！リコが考える！」

そういって彼女はホワイトボードマーカーを手に取る。

リコ「さっきと同じように考えると、面積は縦の長さ×横の長さのことだから、

$$
縦の長さ（円）×横の長さ（個）=面積（円×個）
$$

…だと変になっちゃうんだよね。円$${×}$$個なんて単位はないから！
さっきは縦軸の長さの単位が実は$${本/匹}$$だったって話だったから、今回も縦軸の単位が実は$${円/個}$$で、

$$
縦の長さ（円/個）×横の長さ（個）=面積（円）
$$

になるんじゃない？？」

すごいな。
リコの相手をしていると、ときどきあまりの飲み込みの早さに衝撃を受けることがある。退屈なことが嫌いで、忍耐力はないけれど、興味のスイッチが入ると頭の回転がちょっとびっくりするぐらい速くなる。

僕「そう考えると、厳密に言えば縦軸の単位は（円/個）になるね」

コノミ「もっと厳密に言えば、横軸の単位も（個/年）や（個/月）になるわ。期間を区切らないと、需要量を定義できないわ」

リコ「ややこしい…」

コノミ「面積は（円/年）を表す。需要関数は縦軸の長さが決まると横軸の長さが決まる関数だから、価格を決めると需要量――つまり、可能な最大の販売量が決まって、同時に価格$${×}$$販売量$${=}$$売上が決まる」

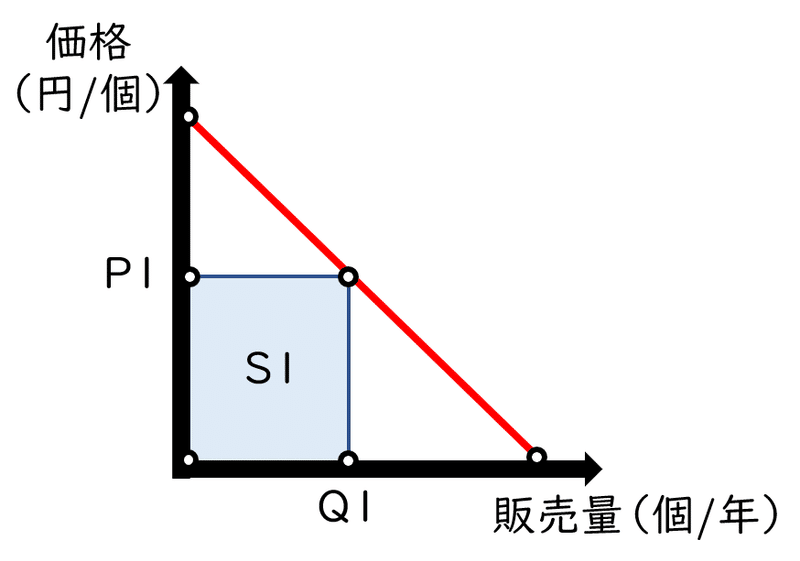
リコ「QとSは何のイニシャル？」

僕「Qは量を意味するQuantity、Sは売上を意味するSalesだね」

コノミ「さて、ここで企業にとっての最適化問題を考えることができる。つまり、ある価格で販売したらどれだけの販売量が見込めるかがわかっているとき、売上を最大化する価格がいくらなのかを考えることができる」

リコ「リコこういう問題知ってる！辺上を動く点P！」

…！！
確かに、似たような図形の問題を見たことがあるぞ。

中学数学の七不思議のひとつ、謎の動く点Pがこんなところで関係してくるなんて…。
「数学は異なるものを同じとみなす技術である」という言葉を思い出す。確か、位相幾何学の創始者アンリ・ポアンカレの言葉だったか。

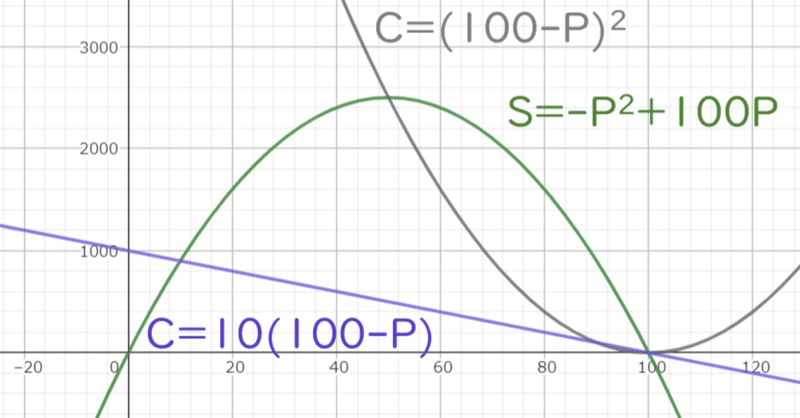
僕「この問題は二次関数の最大値を求める問題として処理できるね。需要関数を$${Q=1000-P}$$として、

$$
S=P×Q
$$

に$${Q=1000-P}$$を代入すると、SをQの二次関数で表せる。

$$
S=P(1000-P)=-P^2+1000P
$$

二次関数の最大値を求める問題は、式を平方完成すれば求めることができるね。

$$
S=-(P-500)^2+250000
$$

Sが最大値を取るのは$${P=500円/個}$$のとき、最大値は250000円だ」

コノミ「価格を横軸、売上を縦軸にとると、上に凸の二次関数を描けるわね」

コノミ「上に凸のグラフになるということがわかっていれば、微分という手続きを用いて最大値を求めることもできるわ」

僕「微分って、確か高校で習うやつだよね。確か、二次関数を微分すると接戦の傾きがわかるんだよね」

コノミ「微分は極限（lim）を使って定義される。

$$
\frac{df(x)}{dx}=\lim_{n \to 0}\frac{f(x+k)-f(x)}{k}
$$

式はともかく、大事なのは図形的なイメージね。下の図のkをどんどん小さくしていくと、横軸の座標がxのときのグラフの傾き――つまり縦軸の瞬間的変化がわかるわ。

そして、グラフの最大値では瞬間的な変化――つまり、接線の傾きがゼロになる。

微分の具体的な式変形は高校数学で習うとしても、基本的なアイデアは知っておいて損はないわ。経済学者は最大値を求めるときに微分を用いる」

僕「上に凸のグラフであるっていう前提は必要になるよね。でも、平方完成でもいいのに、なんでわざわざ微分なんていう難しい技を使うの？」

コノミ「平方完成は二次関数の場合にしか使うことができないわ。本格的な経済学は様々な形の関数を扱うから、上に凸の場合に広く使える微分の方が便利なの。売上が価格の二次関数にならないケースを、ひとつ見てみよう。

需要関数が$${Q=1000/P}$$で表されるとき、売上を最大化する価格はいくらになるか。これは、リコでも解けるんじゃない？」

リコ「ええ！？こんな問題やったことないよー」

コノミ「計算はそんなに難しくない。丁寧に式を追っていけば大丈夫」

リコ「うーん…。売上は$${価格×販売量}$$だから、

$$
S=P×Q
$$

ここに$${Q=1000/P}$$を代入すると…

$$
S=P×1000/P=1000
$$

あれ、これでいいの？Pが消えちゃった」

僕「定数関数だよ。PとQの積が常に等しいとき、2つの変数の関係をなんて言うか覚えてる？」

リコ「あ、反比例！もとの関数が反比例を表しているから積がいつも一緒なんだ！」

コノミ「定数関数を微分すると、xがどの値のときもゼロになる。つまり、xがどの値のときも最大値を取る。このぐらいの式だと微分を使うまでもないように感じるかもしれないけど、異なる形の関数に共通して使えるというのが、微分という技の強みね」

異なる形の関数に共通して使える、か。きっと世の中には僕が知らない関数がたくさんあるから、これはきっとすごく便利なことなんだろうと想像する。

リコ「でも、売上がいつも一緒なんてことあり得るのー？価格を無限に高くしても、逆に『ほぼゼロ円！もってけドロボウ！』みたいにしても売上が変わらないなんて、変なのー」

コノミ「そう、確かにそれは不自然だわ。つまり、反比例の形をした需要関数は現実的ではないということね。想像上の世界で数式として表すことはできるけど、それに対応する現実が常に存在する訳じゃない。思考実験と言い換えてもいいわ」

現実に存在しないものを数式として表すことができるというのは、なんだか世界を創る神様になったみたいでちょっとワクワクする…なんて言ったら、笑われてしまうだろうか。

「下校時間です」

いつの間にか、図書室に夕日が差し込んでいることに気づく。もうそんな時間か。
帰り支度を始めると、コノミがとんでもないことを言い出した。

コノミ「今日は宿題を出しましょう」

◎　◎　◎

夜。帰り際にコノミに出された宿題と、自室でひとり向き合う。図書室でみんなと話しながら考える時間も楽しいけれど、ひとりで静かに問題と向き合う時間も悪くない。

（1）は昼間に考えたのと同じ問題だ。需要関数$${Q=100-P}$$を売上を表す式$${S=P×Q}$$に代入して、

$$
S=P(100-P)=-P^2+100P=-(P-50)^2+2500
$$

を得る。最大値は、$${P=50}$$のとき2500だ。

（2）は…生産費用Cが登場している。なるほど、販売量がひとつに定まるとそれに対応して生産費用がひとつに定まるから、生産費用が販売量の関数として表される――費用関数を定めることができるんだ。
これも、順に式変形していけば解けるはずだ。

利益を表す式$${B=S-C}$$に、

$$
S=P(100-P)=-P^2+100P\\
C=10Q=10(100-P)=-10P+1000
$$

を代入して

$$
B=-P^2+110P-1000=-(P-55)^2+2025
$$

を得る。最大値は、$${P=55}$$のとき2025だ。

（3）も同様に、利益を表す式$${B=S-C}$$に、

$$
S=P(100-P)=-P^2+100P\\
C=Q^2=(100-P)^2=P^2-200P+10000
$$

を代入して

$$
B=-2P^2+300P-10000=-2(P-75)^2+1250
$$

を得る。最大値は、$${P=75}$$のとき1250だ。
一応すべて「代入して平方完成」というシンプルな手続きで解くことができた。けど、なんだかイメージがわかないな。費用関数という新しいキャラクターが登場したけど、なんだかまだピンとこない。

彼女は費用関数を使ってどんな話をするのだろう？

◎　◎　◎

僕「…という感じで、パワープレーだけど一応すべての問題を解くことができたよ」

図書室のホワイトボードで、昨日の夜考えたことを一通り説明した。
リコは僕とは別の宿題――二次関数のグラフを描く宿題を出されたようで、昨日よりは話についてこれたようだ。平方完成の式変形についても、簡単に教えてあげた。

僕「解けたはのはいいんだけど、なんかあんまりすっきりしないんだよね。合っているのかどうかもわからないし、何より2種類の費用関数がそれぞれどんな意味を持っているのかがピンとこない」

コノミ「君は、費用関数のグラフは書かなかったの？」

僕「一応書いてみたけど…」

リコ「CがSより大きくなってるところがあるよ？$${S-C}$$がマイナスになっちゃう」

僕「それは、利益がマイナス――つまり赤字ってことだね。価格が低すぎると、費用の方が大きくなってしまって赤字になってしまうことがある、というのはイメージ通りだ」

コノミ「うん、確かに価格と費用の関係をグラフで表すとそんな感じになるわね。じゃあ、需要曲線が書かれたグラフ――面積が（円）を表すグラフの上で費用関数を表現するとどうなる？」

ん？どういうことだ？

コノミ「費用関数$${C=10Q}$$を考えよう。Cの単位が（円）、Qの単位が（個）ということは、定数である10の単位が（円/個）じゃないとおかしいわね。ということは、この費用関数は

$$
C（円）=10（円/個）×Q（個）
$$

と書ける。つまり、定数10が商品ひとつあたりの生産費用を表しているわ。経済学の世界では、『商品を”もう一つ”作るのにかかる費用』を限界費用(Marginal Cost)と呼ぶ。限界費用は『費用の瞬間的な変化』だから、費用関数を微分することでも得られるわ。

10（円/個）を縦軸に、Q（個）を横軸に取れば、これを限界費用関数として需要関数のグラフと重ねて表すことができるわ。

価格がP、販売量がQのとき、費用と利益は図のように表される」

確かに、単位が（円）になる費用と利益が面積として表されていて、$${利益（B）=売上（S）-費用（C）}$$も成立している。

僕「これなら、辺上を動く点Pの問題と考えることもできるのか。長方形Bの縦の長さが$${P-10}$$、横の長さが$${Q=100-P}$$だから、

$$
B=(P-10)(100-P)
$$

の最大値を求める問題に帰着できるね。リコは解ける？」

リコ「まず、因数分解して$${B=-P^2+110P-1000}$$になって、平方完成すると…」

リコが昨晩に練習したという平方完成の計算を披露する。

リコ「本当だ！$${B=-(P-55)^2+2025}$$になる！」

コノミ「限界費用曲線を導入することで、利益の最大化問題を図形的に把握することができるわ」

僕「費用関数が$${C=Q^2}$$で表される場合は、限界費用関数はどうなるんだろう？」

コノミ「費用関数$${C=Q^2}$$は、

$$
C（円）=Q（円/個）×Q（個）
$$

と書ける。つまり、商品ひとつあたりの生産費用が販売量と比例する――作れば作るほど”作るのが大変になる”状態を意味しているわ。

限界費用関数$${MC=2Q}$$は費用関数$${C=Q^2}$$を微分することによって得られるけど、ここでは三角形の面積で表される費用Cが$${Q×2Q÷2=Q^2}$$であることが確認できれば良いわ」

僕「これも一応、辺上を動く点Pの問題にして解けそうだね」

リコ「驚愕！」

◎　◎　◎

コノミ「今日やった売上や利益の最大化問題は、経済学の土台を成す最適化問題――optimization problemの一種だ。経済学者はこの世界に無数に存在する人々の行動を予測するために、大胆な仮定を置いた。すなわち、人や企業は常に自分たちの行動を最適化している、最適化問題の解を選択しているという仮定ね」

帰り道。今日もまた、僕とコノミの2人で駅までの道を歩く。暗めの茶髪が夕日を少しだけ反射し、海風になびいていて――なんだか絵になるな、と思った。

僕「それは強すぎる仮定なんじゃないかな。確かに企業は売上を最大化するのが理想だと思うけど、実際には需要曲線の形はもっと複雑かもしれないし、そもそも需要曲線がどんな形をしているかわからない。企業が最適化問題の解を選択できているという仮定は、非現実的だと思うけど…」

コノミ「そう、人や企業が最適化問題の解を選択しているというのは、非現実的で大胆な仮定だ。
でも、大胆な仮定を置くからこそ広がる世界がある。――経済学の本質は、その認識論的特質にあると言ってもいい。
大胆な仮定を置くことで、経済現象を予測したり、政策の効果や良し悪しを判断したりすることができる。
それがいつも現実と整合するとは限らないけれど、現実をただ”書き写す”だけではわからないことがたくさんある。だから経済学者は、大胆な仮定を置き、未来を予測し、政策を評価し――そしてときに間違う」

高架下。車の音で声がかき消されるから、ここを通るときはいつも会話が中断される。彼女の目はまっすぐ前を向いていた。次にいったい何を言うんだろう。

コノミ「もちろん、最適化の仮定が強すぎるといって主流派の経済学を批判するグループもある。
それでも、経済学者はときに間違いながらも、大胆な仮定を置いて未来を予測することを続けてきた。

経済学は攻めの学問だ。

現実的に即して毒にも薬にもならない事実を述べることよりも、多少非現実的な仮定を置いてでも政策的含意のある結論を導くことを重視する。

…そのためには、世界の幸福量を評価する基準である”余剰”を導入しなければならない。いつかその話をしよう」

非現実的な仮定でもいい。
現実に即して事実を述べることよりも、政策的含意がある結論を導くことを重視する。
――経済学は攻めの学問だ。

それがいったいどういうことなのか、今の僕には完全にはわからないけれど、なんだかとてもワクワクすることだけは確かだ。

――大胆さという武器は、僕らをどこに連れていってくれるのだろう？