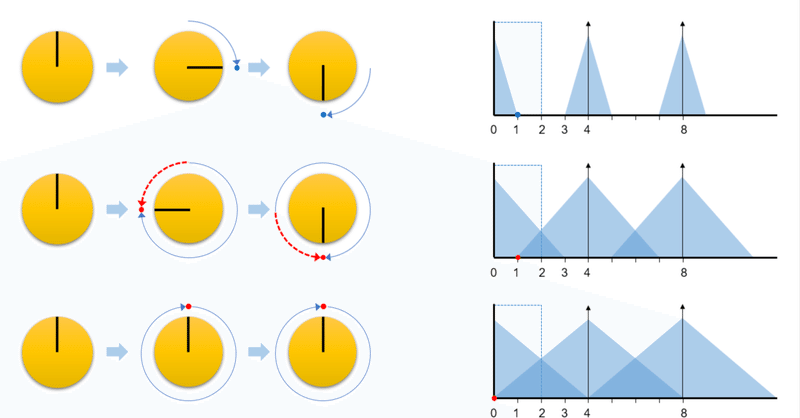
折り返し雑音とは?~なぜ車のホイールは逆回転するのか~デジタルはアナログの近似ではない
電子書籍発売しました!(2023/01/22)
動画・音声リンク付き紹介記事はこちら。
Amazon Kindle 電子書籍「MATLAB で簡単オーディオ プラグイン開発」
スクリプトはどなたでも無料でダウンロードできます。
折り返し雑音(aliasing noise/aliasing artifact/folding noise)
信号処理の経験がない人には耳慣れない言葉かもしれませんが、ほぼ全ての人がその現象を見たことはあるはずです。
TVや映画などで、車などが走り出すときを思い出してください。
車自体のスピードは段々上がっているにもかかわらず、ホイールの回転がゆっくりになったり、止まったり、逆回転しているように見える「アレ」が折り返し雑音です。
ホイールが逆回転する理由
TVや映画は、1秒間に24/30/60/120枚とかの静止画を連続再生して動画として見せています。
その間の画はなく、飛び飛びです。
回転するホイールを、4回/秒観測する場合を考えてみましょう。
まずは1秒間に1回転する場合、観測する度に1/4回転することになります。
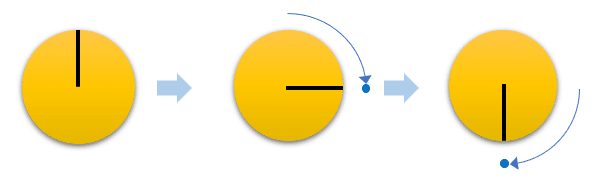
この場合、正しく回転しているように見えます。
これが回転速度が上がり3回転/秒になると、観測する度に3/4回転していることになります。この場合、逆回転の方が変化が少ないので、人の目には逆方向に1回転/秒しているように見えてしまいます。
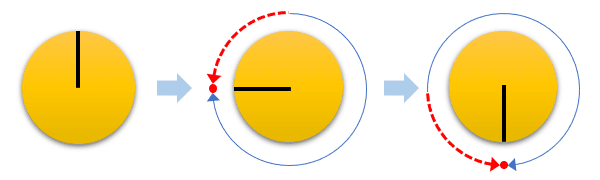
さらに速度が上がり4回転/秒になると、観測間隔と回転スピードが同期するので、人の目には止まっているように見えてしまいます。
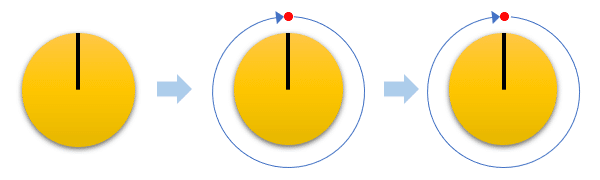
この様な理由で、ホイールの回転がゆっくりになったり、止まったり、逆回転しているように見えるのです。
実際に、時計回りに回転速度を上げている例を示しておきます。

以下、もう少し技術的に見ていきましょう。
フーリエ変換の双対性
デジタル信号処理は数学です。
デジタルは、適当に作ってもなんとなく動いているように見えたりもしますが、逆に言うと、作った通りにしか動きません。正確に作れば正確に動きます。そのため、数学的な考察は重要です。
とはいえ、まずはイメージを持つことが大切ですので、ここでは結果だけを述べます。数学的な話はAppendixを参照してください。
フーリエ変換/逆フーリエ変換により時間軸と周波数軸の変換が行えますが、その性質から、時間軸と周波数軸には以下のような関係性が成り立ちます。
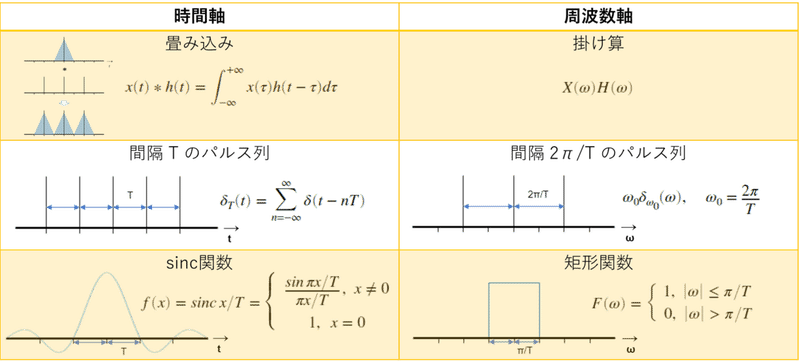
また、時間軸→周波数軸 で成り立つことは 周波数軸→時間軸 でも成り立ちます。(双対性)
標本化(Sampling)
アナログ信号をデジタル信号に変換するための時間方向の離散化を、標本化と言います。(レベル方向の離散化は、量子化と言います)
標本化を行うための標本化パルス列(サンプリング関数)として、一定間隔Tのパルス列を用いるとします。(サンプリング周波数 Fs=1/T )
スペクトルは、音声信号等であれば一般的に高域に行くにしたがってパワーは小さくなるので、ここでは三角形で表します。
標本化は、時間軸で元信号とサンプリング関数を掛け算すればできますね。
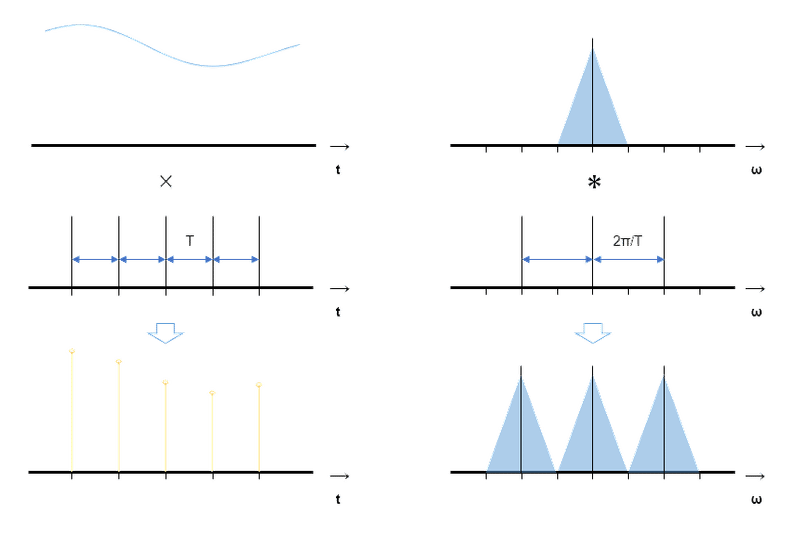
左:時間軸、右:周波数軸
1段目:アナログ元信号
2段目:サンプリング関数
3段目:サンプリング結果(デジタル信号)
周波数軸では、元信号のスペクトルと周波数軸上のサンプリング関数との畳み込みになります。
したがって、デジタル信号にするために離散化を行うと、周波数軸上では元信号のスペクトルのイメージ成分が無限に現れることになります。
この時、元信号のスペクトルが1/(2T)を超えていると、信号成分とイメージ成分が重なってしまいます。(ω=2πf)
先ほどのホイールの例で見てみましょう。
1回転/秒の場合
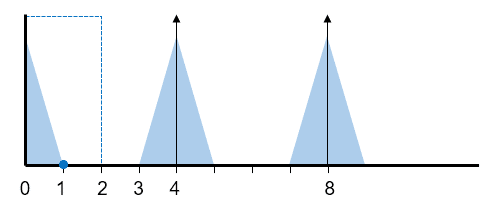
回転速度が上がり、3回転/秒の場合
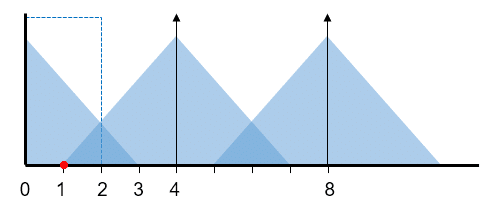
イメージ成分が折り返り、反転して1のところに入ってきます。
元の信号とイメージ成分は見分けが付かないため、これが逆方向に1回転/秒しているように見えています。
さらに速度が上がり、4回転/秒
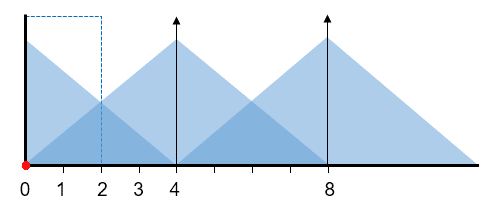
周波数=0 のところに折り返ってくるので、止まっているように見えます。
つまり、サンプリング周波数が4Hzの場合、その半分の2Hz以上になるとイメージ成分と区別が付かなくなると言うことです。よって、点線で囲った2Hz未満が観測される範囲となります。
また、上の一連の図から、元信号のスペクトルがFs/2未満に収まっていればスペクトルが重ならないので、後でその部分を取り出すことができれば、元の信号に戻せることがイメージできるのではないでしょうか。
図で示すと以下のようになります。
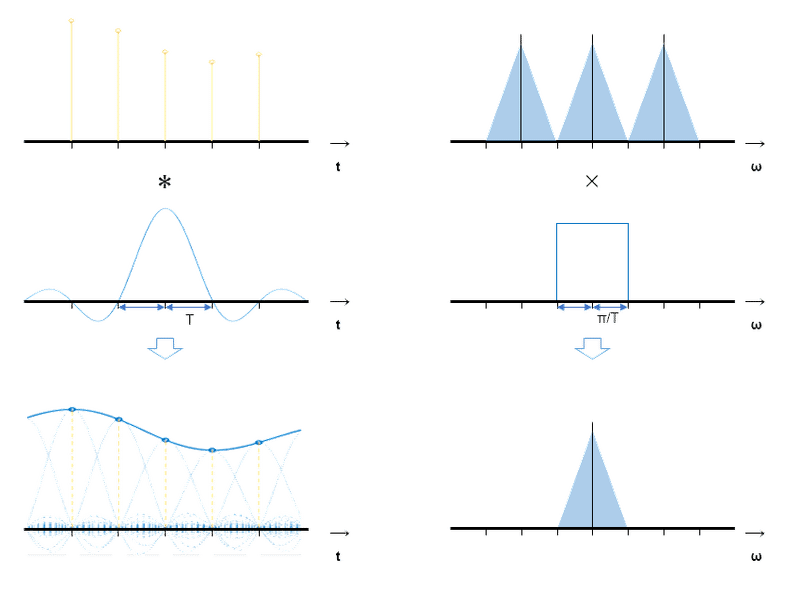
左:時間軸、右:周波数軸
1段目:デジタル信号
2段目:理想LPF(時間軸ではsinc関数)
3段目:復元されたアナログ信号
矩形関数である理想LPF特性の逆フーリエ変換はsinc関数になるので、各サンプル値とsinc関数の畳み込み積分で元信号が復元されます。
これが、標本化定理であり、
「最高周波数(広義には信号帯域)がFs/2未満の信号であれば、サンプリング周波数Fs以上の標本化によって情報の消失なしに離散化できる」、ということを示しています。(Fs=1/T)
アナログ<->デジタル信号の変換で、サンプリング周波数を上げればいくらでも精度が上がりそうに思えるかもしれませんがそうではなく、元信号帯域がある範囲に収まっていれば、その倍を超える周波数でサンプリングを行えば、(原理的には)アナログ信号とデジタル信号は一意に変換できると言うことです。
別の言い方をすると、「デジタル信号はデータが時間的に飛び飛びなので、その間は適当に繋ぐしかなく、元のアナログ信号とは異なる」というのは誤解、ということになります。
間の値は、適当な値でも、ましてや決して直線でもなく、sin(x)/x(の積分)で決まるただ一つの曲線です。
現実的には、理想LPFは無限タップ長となるため完全には作れませんしデバイスの精度等色々と問題もありますが、原理的な問題とは切り離して考える必要があります。
折り返し雑音を見てみよう
この図は、CZP(Circuler Zone Plate)と呼ばれる、x/y軸と周波数変化を一致させたテストパターンです。これを入力画像として用いれば、システムの周波数特性が目で見てすぐ分かります。
目がチカチカするかもしれませんので、
「部屋を明るくしてモニターから離れてご覧下さい」

MATLABで書くとこんな感じ。
N = 200; a = 2;
[x,y] = meshgrid(-N:N);
r = sqrt(abs(x).^2 + abs(y).^2);
czp = sin( (pi * r.^2) / (a * max(r(:))) );
czp = czp(1:N*2,1:N*2);
czp = czp-min(czp(:));
czp = czp/max(czp(:));
imshow(czp)sinの位相項にx/yが入るので^2になります。
最近のオーディオ測定系では、CZPの発展型とも言えるSwept-Sine(旧TSP(Time Stretched Pulse))が用いられることも多いですね。
オフライン測定以外でも、伝達関数を解析的に求めるのが困難な場合等に、Swept-Sineを入力として通せば周波数特性を簡単に求めることもできますし、安定かどうかもすぐ分かります。
では、CZPを縦縞を使って上半分だけサンプリングしてみましょう。
まずはこちら。

このサンプリングパターンを、上のCZPと重ねます。

CZPとサンプリングパターンの周波数が一致した部分(とその整数倍位置)に、折り返しとしてCZPの中心と同じ模様が現れます。
次はもっと細かいパターン。


縦線間隔がサンプリング周波数になりますので、間隔が細かいパターンと重ねると、折り返しも高域に移動します。
(必ず100%表示で見てください)
一応、Simulinkモデル(R2020b)も。
下の図はPhotoshopで、それぞれNearestNeighbor、Bi-Linear、Bi-Quad法を用いて縦横半分に縮小したものです。それぞれのフィルター特性の違いが分かるかと思います。

Appendix
CDのサンプリングレートはなぜ44.1kHz?
なぜ、こんな中途半端な数字なのでしょうか?
これは、ソニーが開発した最初の頃のPCMレコーダーが、ビデオデッキを元に作られたためです。
可聴帯域である~20kHzを記録するには数MHzの(当時としては)広帯域が必要でアナログテープレコーダーに記録することはできず、VCRの記録機構をそのまま流用しました。
回転ヘッドでヘリカルスキャンしながら記録・再生するのですが、アナログTVの水平同期周波数は15.75kHzで、ここに16ビットステレオ3サンプル分の記録が可能でした。
回転ヘッドで記録可能な時間は全体の14/15であったので、
15.75*14/15*3 = 44.1(kHz)
と自動的に決まりました。
これ以外やりようがなかったとも言えるでしょう。
サンプリングレート変換
アナログよりも複雑な処理が正確に安定して行えるのがデジタル信号処理の特徴ですが、苦手な処理の一つにサンプリングレート変換があります。
例えば、CDの44.1kHzデータをDVD等の48kHzに変換する場合を考えてみましょう。
44.1:48 = 147:160
ですから、原理に従えば、
・一旦160倍に補間してデータ数を増やす
・補間フィルター処理を行う
・147個ごとにデータを間引く
という処理を行う必要があります。
イメージ成分を綺麗に取り除くためのフィルターは、24ビット精度を保持しようとすれば、160倍の高い動作周波数上で2~3万タップのFIRが必要となります。
そのため、sin(x)/xではなく他の次数の低い補間関数で代用することも多く、その場合はかなり音質が変わってしまいます。
PC等で作業をしていると、意図せずそういったレート変換が入って音質劣化を起こしている場合も多いので、気を付けましょう。
ビデオとの同期を取るためジッターリデューサーとしての機能を持つ非同期式レートコンバーターもありますが、それはいわば音質を変えることによってジッターを吸収しているわけですから、取り扱いには注意が必要です。
マルチステージフィルターやポリフェーズフィルターを駆使すれば、比較的少ない演算量で原理通りの処理を行い、音質変化のほとんどない変換を行うことは可能です。
20年以上前に実機を開発し、レコーディングエンジニアの方々のブラインドテストでも
「(それまで最も音質変化の少ない方法であった、それぞれ100万円くらいする)D/A->A/Dの組み合わせよりも音質変化が少ない」
との評価でした。
某レコーディングスタジオに無期限貸出ししてたので、実際にそれを使ってたくさんのCDが制作されたと後から聞きましたが(96kHzでレコーディングしてCD化)、どこに行ったのかな、あれ・・?(¬_¬)
デジタルデータが同じなら音も同じ?
デジタルデータが同一なら、音も変わらないのでしょうか?
オカルトチックに?よく議論されていますが、見逃されがちなのが「クロック」の問題です。
デジタルデータのまま音は聞けないので、アナログに変換する必要があります。このときデータ以外に必要になるのが、各データをアナログに変換するタイミングを決定するクロックです。このタイミングが揺らいだりすると、聞こえる音も当然変わってしまいます。
このクロックジッターは電源電圧の変動等の影響を受けます。
「音の良いSD」なんてのもありましたが、わざと読み込み速度を落としたりして、電源電圧変動を抑えているのかもしれませんね。
他にも、直接的ではないノイズの影響もあります。
不快なノイズが聞こえると脳は無意識にそのノイズを消そうとして、最低可聴限界レベルを引き上げます。
高域にノイズが乗っても、全体の可聴限界レベルが上がるため、結果として低域も聞こえにくくなってしまいます。
例えばCDプレイヤーの電源を入れると、モーターが回転して高域ノイズが発生します。通常は注意して聞かないと分からない程度の音量なのですが、脳は敏感に反応してノイズを抑えにかかり、直接関係のない普通の話声の低音も聞こえにくくなったりします。
オーディオは奥が深いですね・・。
数学的補足
本編で説明を飛ばしたところを、数式を使って簡単に説明しておきます。
・フーリエ変換
デジタル信号処理は、フーリエ変換がなければ始まりません。
フーリエ変換/逆フーリエ変換の定義式は以下の通りです。
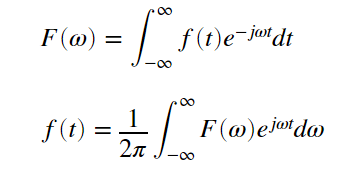
・インパルス応答と伝達関数
時系列信号xを、伝達関数Hのシステムに入力した場合を考えます。
伝達関数 H(ω) は、そのシステムにδ関数(インパルス関数)を入力したときの応答(インパルス応答)のフーリエ変換(ラプラス変換)で表されます。
インパルス応答は、デジタルで考えるとこんなイメージです。
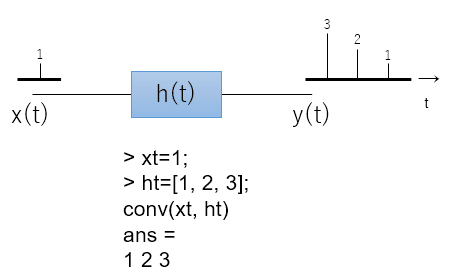
・δ関数
δ関数は超関数の一つです。超関数とは、計算を矛盾なく便利にするために導入された特別な性質を持つ関数のことをいいます。
定義は
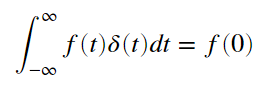
で、以下のように読み替えることができます。
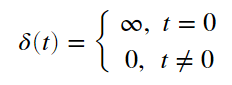
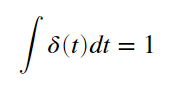
0でのみ値を持ちその値は∞であるが面積は1、という、普通にはあり得ない関数です。あくまでも全区間積分が1であり、t=0でしか値を持たないのですが、δ(0)=1ではないのが超関数たる所以です。(幅が0なので、δ(0)=1を積分したら0になってしまう)
δ関数のフーリエ変換は
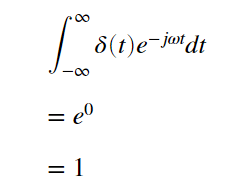
と簡単に計算できますが、"1"は絶対可積分ではないので、普通に計算しようとしたら "1"のフーリエ変換は定義されません。
しかし、δ関数の逆フーリエ変換も同様に1/2πと求まるので、フーリエ変換、逆変換をそれぞれ
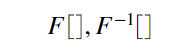
と書くと、δ関数の逆フーリエ変換の両辺をそれぞれフーリエ変換すれば、
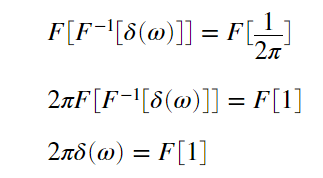
と、1のフーリエ変換が求まります。
・畳み込み(convolution)
一般的なデジタルシステムは、線形で時不変である線形時不変(LTI)システムとして考えます。
インパルス応答 h(t) のLTIシステムに 時系列信号 x(t) を入力した場合の出力 y(t) は
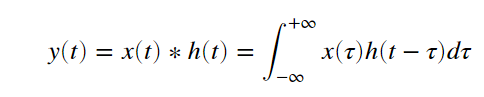
で表され、これを畳み込み(convolution)と呼びます。
畳み込みのデジタルでのイメージはこんな感じ。
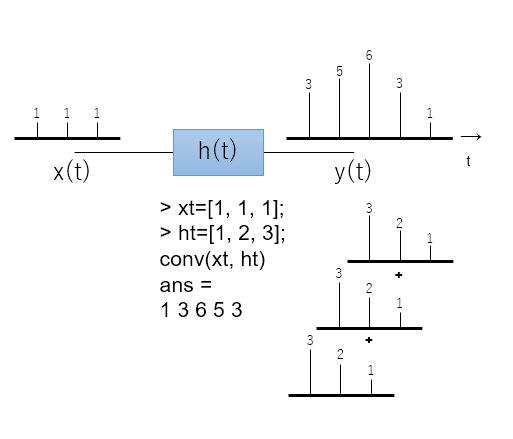
さらに、畳み込みのフーリエ変換を考えます。
畳み込みの定義式は
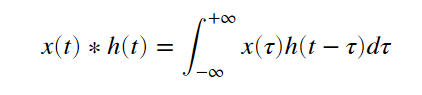
ですのでそのフーリエ変換は、
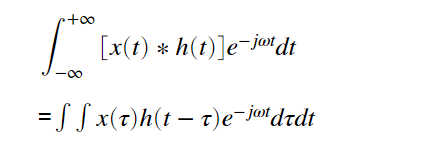
ここで、
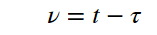
と置くと、
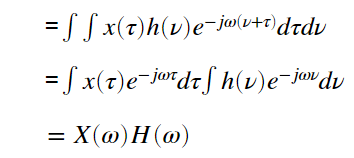
となり、畳み込みのフーリエ変換は、それぞれのフーリエ変換の掛け算となることが分かります。これは逆も成り立ち、掛け算のフーリエ変換はそれぞれのフーリエ変換の畳み込みとなります(双対性)。
システムの出力は、入力時系列信号 x(t) と システムのインパルス応答 h(t) の畳み込み、あるいは入力スペクトル X(ω) とシステムの伝達関数 H(ω) の積で表されるということです。
時間軸と周波数軸はフーリエ変換の関係にあるので、
時間軸での畳み込み = 周波数軸での掛け算
時間軸での掛け算 = 周波数軸での畳み込み
が成り立ちます。
・矩形関数とsinc関数
矩形関数
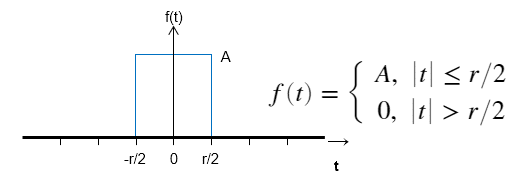
のフーリエ変換は、
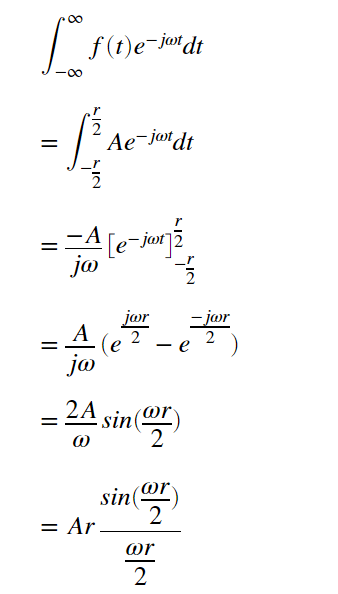
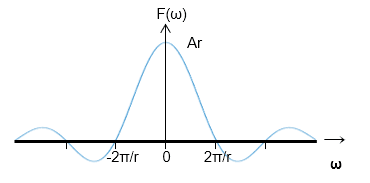
と、
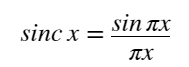
の形になります。
ロピタルの定理により、sinc(0)=1 です。
MATLABとかにはsinc関数があるので、極限値とかは気にせず使うことができます。
・サンプリング関数
標本化パルス列(サンプリング関数、Comb関数)はδ(t)を用いて
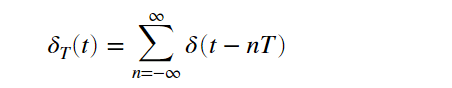
と表されます。
周期Tの関数であるので、フーリエ級数展開を用い
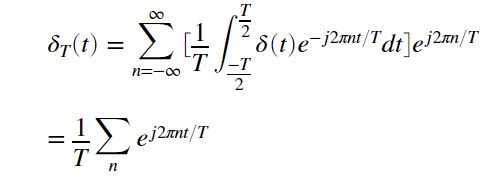
ここで、
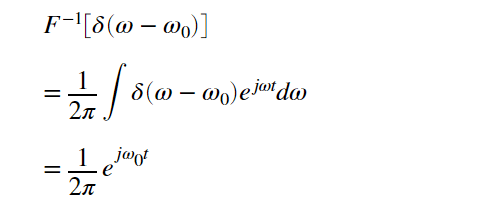
なので
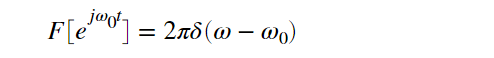
が成り立ちます。
これを使うと、標本化パルス列のフーリエ変換は
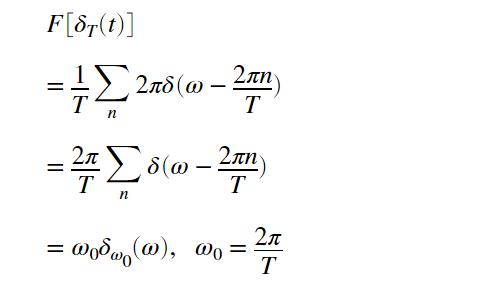
となり、間隔Tのパルス列のフーリエ変換は、間隔2π/Tのパルス列となることが分かります。
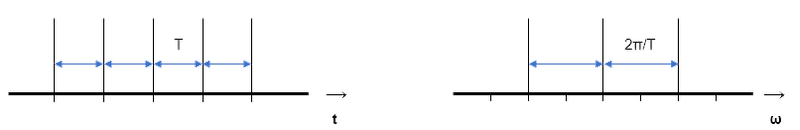
・標本化定理の数式表現
帯域幅 W=Fs/2 未満に制限された信号 f(t) は、サンプル間隔 τ=π/Wのサンプル値 f(n) のみで以下のように再現されます。
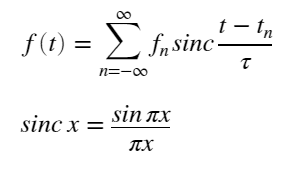
以上、ざっくりした感じですが、一度自分で数式を解いてみると理解が深まる(分かった気になる ←これ重要)と思います。
とは言いつつも、私も数学が得意なわけではないので、間違い等あればご指摘ください。(¬_¬)
では。
この記事が気に入ったらサポートをしてみませんか?
