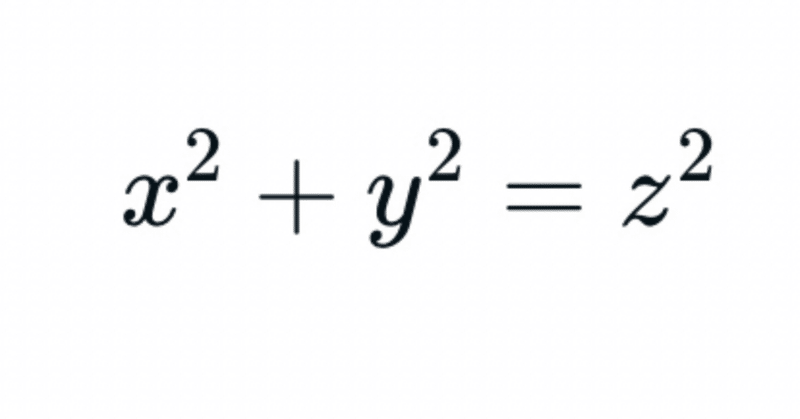
Mathematics short story #5
-------------------------------------------------
$${Published}$$ $${Online}$$ $${First}$$ $${(21/2/2024)}$$
$${Latest}$$ $${additions}$$ $${(21/2/2024)}$$
-------------------------------------------------
数学のどうでもいい小話シリーズ #5
前回・前々回で既約ピタゴラス数の求め方を
$${2}$$通り紹介しました
今回はそんなピタゴラス数の面白い(?)性質を
調べてみたいと思います
面白くないと思った方は我慢😣して下さい
-------------------------------------------------
【おさらい】
原始ピタゴラス数$${(a, b, c)}$$
ピタゴラスの公式
$${(a,b,c)=(m^2-n^2,2mn,m^2+n^2)}$$または$${(2mn, m^2-n^2, m^2+n^2)}$$
$${m > n}$$で$${m, n}$$は互いに素な偶奇の異なる自然数
ブラフマグプタの式
$${(a,b,c)= \biggl(kl,\dfrac{k^2-l^2}{2},\dfrac{k^2+l^2}{2} \biggl)}$$または
$${(a,b,c)= \biggl(\dfrac{k^2-l^2}{2},kl,\dfrac{k^2+l^2}{2} \biggl)}$$
$${k > l}$$で$${k,l}$$は互いに素な奇数
-------------------------------------------------
【面白い性質$${1}$$】
原始ピタゴラス数$${(a, b, c)}$$は
$${(a,b)}$$の一方は$${3}$$の倍数である
$${(a,b)}$$の一方は$${4}$$の倍数である
$${(a,b,c)}$$の一つは$${5}$$の倍数である
つまり$${3}$$数の積$${abc}$$は$${60}$$の倍数になる
ここまではどの本にもよく書かれています
もう一歩前に進んでみましょう
$${(a,b,a-b,a+b)}$$の一つは$${7}$$の倍数である
-------------------------------------------------
【$${3}$$の倍数の証明】
$${(a,b)}$$のどれも$${3}$$の倍数でないとすると、$${a^2,b^2}$$を$${3}$$で割った余りは、必ず$${1}$$となる
したがって、$${a^2+b^2}$$を$${3}$$で割った余りは、$${2}$$となるが、$${a^2+b^2=c^2}$$を$${3}$$で割った余りは$${0}$$か$${1}$$なので、これは矛盾である
したがって$${(a,b)}$$の一方は$${3}$$の倍数である
という事は$${c}$$は$${3}$$の倍数ではない
-------------------------------------------------
【 $${4}$$の倍数の証明】
$${(a,b,c)=(m^2-n^2,2mn,m^2+n^2)}$$
$${m, n}$$は互いに素な偶奇の異なる自然数なので$${2mn}$$が$${4}$$の倍数である
-------------------------------------------------
【$${5}$$の倍数の証明】
$${(a,b,c)}$$のどれも$${5}$$の倍数でないとすると、$${a^2,b^2,c^2}$$を$${5}$$で割った余りは、$${1}$$か$${4}$$となる
したがって、$${a^2+b^2}$$を$${5}$$で割った余りは、$${0}$$か$${2}$$か$${3}$$となるが、これは、$${a^2+b^2=c^2}$$であることに矛盾である
したがって、$${(a,b,c)}$$の一つは$${5}$$の倍数である
-------------------------------------------------
【積$${abc}$$が$${60}$$の倍数の証明】
$${\gcd(a,b,c)=1}$$なので$${3•4•5=60}$$の倍数になる
-------------------------------------------------
【$${7}$$の倍数の証明】
$${(a,b,c)}$$の$${b}$$を偶数とする
自然数を$${7}$$で割った余りは次のパターンになる
全て$${\pmod 7}$$とする
$${(7k)^2 \equiv 0}$$
$${(7k+1)^2 \equiv 1}$$
$${(7k+2)^2 \equiv 4}$$
$${(7k+3)^2 \equiv 2}$$
$${(7k+4)^2 \equiv 2}$$
$${(7k+5)^2 \equiv 4}$$
$${(7k+6)^2 \equiv 1}$$
$${c}$$は$${7}$$の倍数ではない
もし$${7}$$の倍数であれば$${c^2 \equiv 0}$$になるが$${a,b}$$が共に$${7}$$の倍数の時しか成立しない→既約解ではない
次に$${(a,b)}$$が$${7}$$の倍数ではないとする
$${c}$$が奇数なので$${c^2 \equiv 1,2,4}$$
$${c \equiv (1,2,4)}$$となる組合せは
$${(a^2,b^2,c^2) \equiv (1,1,2)}$$
$${(a^2,b^2,c^2) \equiv (2,2,4)}$$
$${(a^2,b^2,c^2) \equiv (4,4,1)}$$
この時どの組合せを選んでも
$${(a^2-b^2) \equiv 0}$$になるので
$${(a-b)(a+b) \equiv 0}$$になる
$${(a,b)=1}$$なので$${(a-b,a+b)=1}$$
つまり
$${(a-b,a+b)}$$の一方は$${7}$$の倍数である
$${a,b}$$の一方が$${7}$$の倍数の時は
他方を$${c \equiv (1,2,4)}$$と同じものを選べば良いし
$${(a-b,a+b) \not\equiv 0}$$となる
$${\rm (Q.E.D.)}$$
-------------------------------------------------
斜辺$${c}$$が$${3}$$では割れない事がわかった
でも$${5,13}$$にはなる…
そのあたりのお話しを次回します😊
-------------------------------------------------
続きは #6 へ
バックナンバー
#1・#2・#3・#4
最後まで見て頂きありがとうございました😊
-------------------------------------------------
この記事が気に入ったらサポートをしてみませんか?
