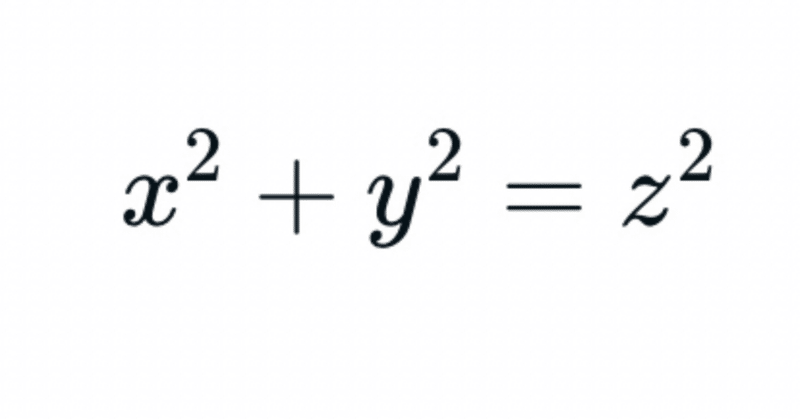
Mathematics short story #6
-------------------------------------------------
$${Published}$$ $${Online}$$ $${First}$$ $${(22/2/2024)}$$
$${Latest}$$ $${additions}$$ $${(22/2/2024)}$$
-------------------------------------------------
数学のどうでもいい小話シリーズ #6
前回に引き続きピタゴラス数の面白い(?)性質を
調べてみたいと思います
面白くないと思った方は我慢😣して下さい
証明はとばしても構いません😊
-------------------------------------------------
【前回までのおさらい】
原始ピタゴラス数$${(a, b, c)}$$の表示方法
ピタゴラスの公式
$${(a,b,c)=(m^2-n^2,2mn,m^2+n^2)}$$
$${m > n}$$で$${m, n}$$は互いに素な偶奇の異なる自然数
ブラフマグプタの式
$${(a,b,c)= \biggl(kl,\dfrac{k^2-l^2}{2},\dfrac{k^2+l^2}{2} \biggl)}$$
$${k > l}$$で$${k,l}$$は互いに素な奇数
$${(a,b)}$$の一方は$${3}$$の倍数
$${(a,b)}$$の一方は$${4}$$の倍数
$${(a,b,c)}$$の一つは$${5}$$の倍数
$${(a,b,a-b,a+b)}$$の一つは$${7}$$の倍数
$${3}$$数の積$${abc}$$は$${60}$$の倍数
-------------------------------------------------
斜辺$${c}$$が$${3,7}$$の倍数ではない事がわかった
でも$${5,13}$$の倍数にはなる…
-------------------------------------------------
【面白い性質$${2}$$】
ピタゴラス数$${(a, b, c)}$$の斜辺$${c}$$
$${\Longleftrightarrow}$$$${c}$$を素因数分解した時に$${\displaystyle p\equiv 1\;(\operatorname {mod} \;4)}$$の素因数を少なくとも$${1}$$つ持つ事である.
-------------------------------------------------
証明する為に下記の【定理1.5】が必要です.
-------------------------------------------------
【定理1.5】(フェルマーの二平方和定理)
奇素数$${p}$$が整数$${x}$$と$${y}$$を用いて、$${\displaystyle p=x^{2}+y^{2}}$$
と表されるのは、$${\displaystyle p\equiv 1{\pmod {4}}.}$$の時に限る.
また逆も成り立つ.この分解は一意的である.
-------------------------------------------------
【定理1.5】を証明する為の若干の準備
-------------------------------------------------
【定義1.5】平方剰余
$${\displaystyle x^{2}\equiv a\;(\operatorname {mod} \;p)}$$を満たす整数$${x}$$が存在する時
$${a}$$は$${p}$$の平方剰余であるといい.
$${\biggl(\dfrac{a}{p} \biggl)=1}$$と表す.
逆に上記の合同式を満たす整数$${x}$$が存在しない時
$${a}$$は$${p}$$の平方剰余でないといい.
$${\biggl(\dfrac{a}{p} \biggl)=-1}$$と表す.
-------------------------------------------------
$${1796}$$年$${4}$$月$${8}$$日
$${\rm Johann~Carl~Friedrich~Gauß}$$
により以下の【定理1.6】が証明された.
(証明は専門書を参照して下さい)
別の機会に投稿すると思いますが今回はパス🙅
-------------------------------------------------
【定理1.6】平方剰余の相互法則
相異なる奇素数$${p,q}$$に対して
$${\displaystyle \left({\frac {p}{q}}\right)\left({\frac {q}{p}}\right)=(-1)^{{\frac {p-1}{2}}\cdot {\frac {q-1}{2}}}.}$$
第$${1}$$補充法則:
$${\displaystyle \left({\frac {-1}{p}}\right)=(-1)^{\frac {p-1}{2}}.}$$
第$${2}$$補充法則:
$${\displaystyle \left({\frac {2}{p}}\right)=(-1)^{\frac {p^{2}-1}{8}}.}$$
また$${p}$$と互いに素な整数$${a,b}$$に対して
$${\displaystyle \left({\frac {ab}{p}}\right)=\left({\frac {a}{p}}\right)\left({\frac {b}{p}}\right)}$$
が成立する.
-------------------------------------------------
ではいよいよ【定理1.5】の証明へ
-------------------------------------------------
[素数についての証明]
平方剰余の相互法則の第$${1}$$補充法則により、
$${\displaystyle p\equiv 1\;(\operatorname {mod} \;4)}$$であれば
$${\displaystyle r^{2}\equiv -1\;(\operatorname {mod} \;p)}$$となる自然数$${r}$$が存在する.
$${\displaystyle 0\leq {x_{i},y_{i}}<{\sqrt {p}}}$$とすると
$${\displaystyle (x_{i},y_{i})}$$の組み合せの個数は$${\displaystyle (\lfloor {\sqrt {p}}\rfloor +1)^{2}>p}$$である.従って$${\displaystyle (x_{1},y_{1})\neq (x_{2},y_{2})}$$で
$${{x_{1}-ry_{1}}\equiv {x_{2}-ry_{2}}\;(\operatorname {mod} \;p)}$$
となるものが存在する.
$${x=|x_{1}-x_{2}|,y=|y_{1}-y_{2}|}$$とすると
$${\displaystyle {\begin{aligned}&{x^{2}}\equiv {r^{2}y^{2}}\equiv {-y^{2}}\;(\operatorname {mod} \;p)\\&{x^{2}+y^{2}}\equiv 0\;(\operatorname {mod} \;p)\end{aligned}}}$$
である.
$${\displaystyle x,y<{\sqrt {p}}}$$であるから
$${0 < x^2+y^2 < 2p}$$であり、故に
$${\displaystyle x^{2}+y^{2}=p}$$である.
[合成数についての証明]
$${\displaystyle p=x^{2}+y^{2},q=x'^{2}+y'^{2}}$$であれば
$${\displaystyle {\begin{aligned}2p&=2(x^{2}+y^{2})=(x-y)^{2}+(x+y)^{2}\\pq&=(x^{2}+y^{2})(x'^{2}+y'^{2})\\&=(xx'-yy')^{2}+(xy'+yx')^{2}\\r^{2}p&=r^{2}(x^{2}+y^{2})=(rx)^{2}+(ry)^{2}\\\end{aligned}}}$$
であるから、十分条件については明らかである.
必要条件については$${\displaystyle A=x^{2}+y^{2}}$$が$${\displaystyle p\equiv 3\;(\operatorname {mod} \;4)}$$の形の
素因数を持つと仮定して矛盾を導く(背理法)
$${\displaystyle p|a}$$であれば$${\displaystyle A=pa=x^{2}+y^{2}}$$と書ける.
ここで$${\displaystyle p|x}$$であれば必然的に$${\displaystyle p|y}$$であり、
$${\displaystyle p^{2}|A}$$であるから両辺を$${\displaystyle p^{2}}$$で除するものとする.
$${\displaystyle p\not |x}$$であれば$${\displaystyle xx^{-1}\equiv 1\;(\operatorname {mod} \;p)}$$となる
$${\displaystyle x^{-1}}$$が存在する.両辺$${\displaystyle (x^{-1})^{2}}$$を乗すると
$${\displaystyle {\begin{aligned}&pa(x^{-1})^{2}=1+(yx^{-1})^{2}\\&0\equiv {1+(yx^{-1})^{2}}\;(\operatorname {mod} \;p)\\&-1\equiv {(yx^{-1})^{2}}\;(\operatorname {mod} \;p)\\\end{aligned}}}$$
となる.しかし、これは
$${\displaystyle -1}$$が$${\displaystyle p\equiv 3\;(\operatorname {mod} \;4)}$$の平方剰余にならないという事実に反する.従って、
$${\displaystyle p\equiv 3\;(\operatorname {mod} \;4)}$$の形の素因数を平方以外の形で持つ合成数が二個の平方数の和で表されることはない.
$${\rm (Q.E.D.)}$$
-------------------------------------------------
ピタゴラス数の斜辺のお話しをしました.
次回は何の話しにしようかな…😊
-------------------------------------------------
続きは #7 へ
バックナンバー
#1・#2・#3・#4・#5
最後まで見て頂きありがとうございました😊
-------------------------------------------------
間違いがあれば教えて頂けますと幸いです🧐
この記事が気に入ったらサポートをしてみませんか?
