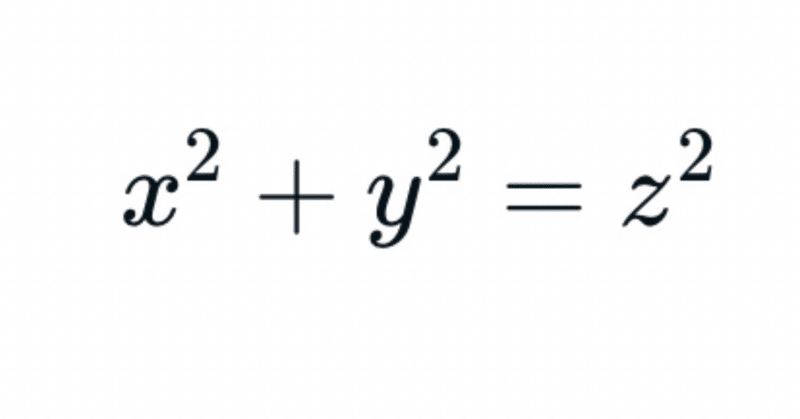
Mathematics short story #4
-------------------------------------------------
$${Published}$$ $${Online}$$ $${First}$$ $${(20/2/2024)}$$
$${Latest}$$ $${additions}$$ $${(20/2/2024)}$$
-------------------------------------------------
数学のどうでもいい小話シリーズ #4
前回は既約ピタゴラス数の求め方を紹介しました
今回はまた別の解の表示を紹介します
結果だけで満足な方は証明をとばして下さい😊
-------------------------------------------------
【定理1.4】既約(原始)ピタゴラス数
$${\rm(primitive~Pythagorean~triple)}$$
$${x^2+y^2=z^2}$$
の既約な整数解$${(a,b,c)}$$は
互いに素な全ての奇数$${k,l}$$を用いて
$${x=kl,y=\dfrac{k^2-l^2}{2} ,z=\dfrac{k^2+l^2}{2}}$$
と表される
これをブラフマグプタの式という
$${\rm (Brahmagupta)}$$
-------------------------------------------------
[証明]
$${x^2+y^2=z^2}$$は、
$${x^2=(z+y)(z-y)}$$と変形できる
ここで、 $${y}$$は偶数、$${x, z}$$は奇数とする
よって、$${u=z+y,v=z-y}$$は共に奇数で
互いに素である
すると、$${x^2=uv}$$となる
したがって、$${u=k^2,v=l^2}$$
となる互いに素な$${k , l}$$が存在する
つまり、
$${x=kl}$$となり
$${y= \dfrac {u-v}{2}= \dfrac {k^2-l^2}{2}}$$
$${z= \dfrac {u+v}{2}= \dfrac {k^2+l^2}{2}}$$
$${k > l}$$
$${\rm (Q.E.D.)}$$
-------------------------------------------------
【まとめ】
原始ピタゴラス数$${(a, b, c)}$$
ピタゴラスの公式
$${(a,b,c)=(m^2-n^2,2mn,m^2+n^2)}$$または$${(2mn, m^2-n^2, m^2+n^2)}$$
$${m > n}$$で$${m, n}$$は互いに素な偶奇の異なる自然数
ブラフマグプタの式
$${(a,b,c)= \biggl(kl,\dfrac{k^2-l^2}{2},\dfrac{k^2+l^2}{2} \biggl)}$$または
$${(a,b,c)= \biggl(\dfrac{k^2-l^2}{2},kl,\dfrac{k^2+l^2}{2} \biggl)}$$
$${k > l}$$で$${k,l}$$は互いに素な奇数
-------------------------------------------------
さてこれで$${2}$$通りの解の表示ができました
次回からはピタゴラス数の面白い🤣性質を
調べていきます
-------------------------------------------------
続きは #5 へ
バックナンバー
#1・#2・#3
最後まで見て頂きありがとうございました😊
-------------------------------------------------
この記事が気に入ったらサポートをしてみませんか?
