対象：理系，文系国立(2次数学利用者，論証出題が多い大学)　

今回は論証です
教科書にもある
$${ax+by=1\ 　(a，b，x，y \ は整数，a \ と\ b \ は互いに素)}$$
についてお話していきましょう
これはベズーの等式($${B\'ezout's \ identity}$$)と呼ばれるもので
教科書では　ユークリッドの互除法の利用　による
手続き的な簡易な説明が載っていたような気がします(数研，今現在は？)
1つの証明は以下のようなものになります

$${a \ と\ b}$$が互いに素ならば，それぞれ何倍かして足せば1になるよ
そして　1が作れるなら，$${n}$$も作れるよ
というものです
自分で思いつくのはちょっと難しい・・・けど，記事を最後まで読めばカンタンになります
そして，互いに素でないときもありました

公約数$${d}$$で割って考えれば①が使えますね

正m/n角形

さて，話は変わって数学の正式な用語かどうかわかりませんが
正$${\dfrac{m}{n}}$$角形　という言葉があります
星形正多角形(regular star polygon)という名前で wiki にはありますね

正多角形というのは　円に内接し
その頂点は円周を$${n}$$等分する点となっています
このとき　辺の長さと弧の長さに着目すると
正3角形　一辺に対する弧の長さが円周の$${\frac{1}{3}}$$
正5角形　一辺に対する弧の長さが円周の$${\frac{1}{5}}$$
というように逆数の関係になっています
すなわち
正$${\frac{5}{2}}$$角形は　一辺に対する弧の長さが円周の$${\frac{2}{5}}$$
ということになっています

正$${\dfrac{m}{n}}$$角形を描くときには
円周を何等分かして(次図では20等分)，ある点をスタートとして
そこから右回り(別に左回りでもよい)に　数個置きに点を結んでいくと書くことができます
スタートを0として右回りに0,1,2,3・・・と番号をふり
例えば 0→7→14→21→28→・・・ のように結んでいくのと同じです
そうすると$${\frac{7}{20}}$$角形ができます

この書き方だと，次のようなばあいもありますね

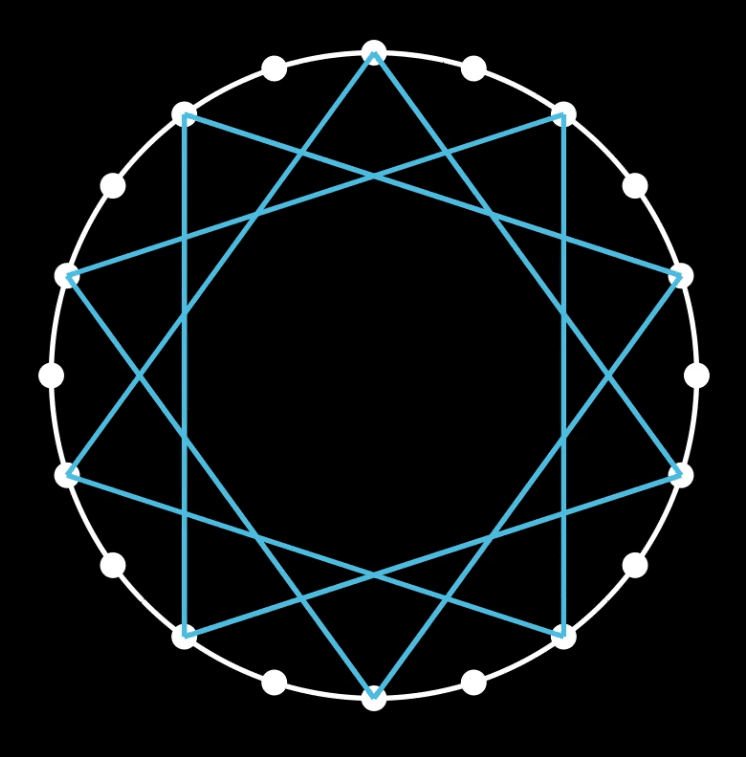
図形的には3種類にわけられます
(ア)普通の正多角形になるもの
(イ)星形正多角形になるが，すべての頂点を経由しないもの
(ウ)すべての頂点を経由する星形正多角形

なぜこのようになるのかはさほど難しくないでしょう
円の$${n}$$等分点と，$${m}$$の倍数を結んでいったとき
(ア)は　$${m \ が\ n \ の約数}$$
(イ)は　$${m \ は\ n \ の約数ではないが，公約数をもつ}$$
(ウ)は　$${m \ と\ n \ は互いに素}$$
となりますね

(ウ)についてちょっと考えてみると
$${m \ と\ n \ は互いに素であるから，最小公倍数は\ mn }$$
　→　元の点にはじめて戻るのは点の番号が$${mn}$$
　→　点の番号は$${(0→)m→2m→・・・→mn(ちょうどm周)}$$
　→　$${n}$$ 個の頂点ができ，途中で同じ点を通過することがない
　→　$${n}$$個の頂点はすべて異なる

のような理解ができます
実は，点にこのように番号をつけていくのは
$${自然数を \ n \ の剰余類　n，n+1，n+2，・・・，n+(n-1)}$$
に分けているのと同じということになります
3進んだ点に着目してみると
この点の番号は，何周もしていくと
$${3→n+3→2n+3→3n+3→・・・}$$
となり，確かに$${n \ で割った余りが3}$$となる自然数になっています
剰余類を図形化したものの1つなんですね

再度　ベズーの等式

この辺りまでくれば，気が付いたひとも多いでしょう
ベズーの等式①は，星形多角形の話に変換すると
$${n\ で割ったときの余りが1(または\ n-1)}$$の点を必ず通るということを述べているので
「全部の点を通るよ」「だから余りが1の点を通るよ」ということを言えばよいのです
これを踏まえてもう一度証明を読み返してみましょう

図形的に一度考え理解できたなら，証明がさほど難しくないように見えてきます
ちなみに(イ)の場合は，ベズーの等式②に対応していますので
考えてみてください

以上　ベズーの等式と正$${\frac{m}{n}}$$角形のお話でした