対象：定期試験以上

今回は　有理関数の積分について学びましょう

有理関数とは　分母と分子が多項式である分数関数のことです
特に　$${\dfrac{(1次以下)/(2次)}$$　について焦点をあてて整理していきます
順を追って基礎からお話しますので　多少長くなります

真分数式化

分母分子が1次式の場合には　分母を1文字$${t}$$で置き換えると積分できる形になります
ただし　2次以上の場合も考えるとやはり「真分数式化」が重要となります

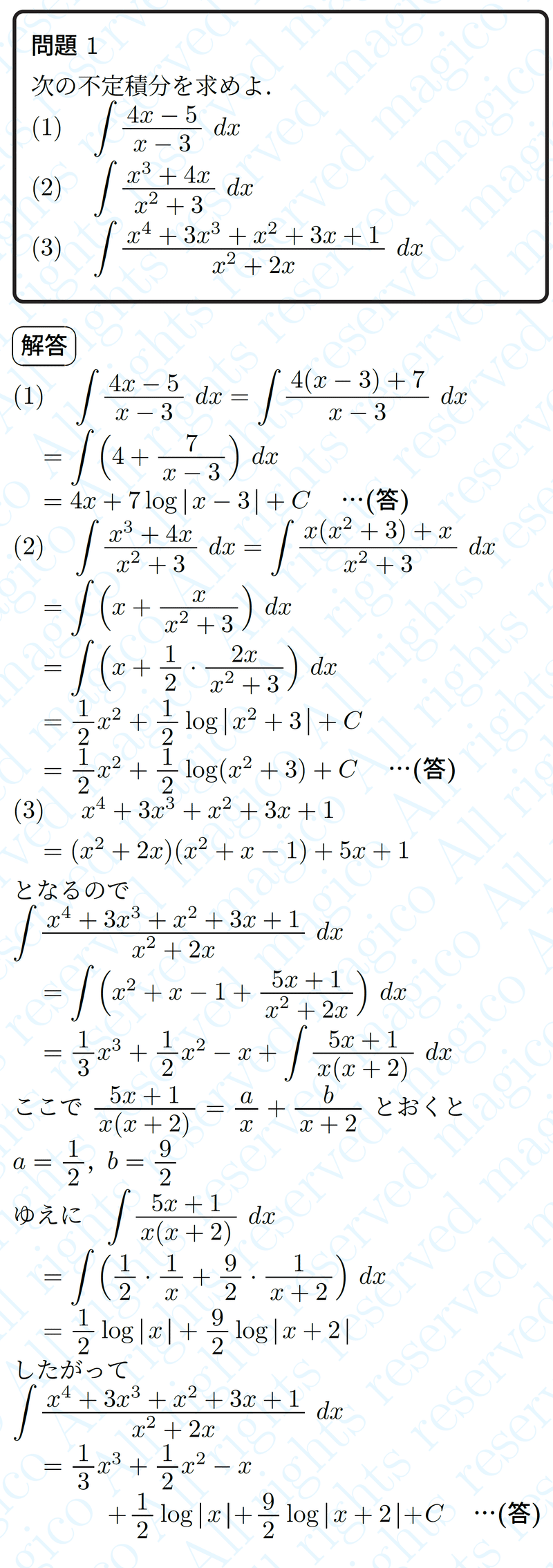
部分分数分解　級数展開と恒等式

さて　$${\dfrac{2次式}{2次式}}$$は真分数式化によって
$${定数+\dfrac{1次以下}{2次式}}$$　とすることができますが
$${\dfrac{1次以下}{2次式}}$$　が　$${\dfrac{f'(x)}{f(x)}}$$　のタイプであれば
対数を用いた　$${\log |f(x)|}$$　となります

一方　$${\dfrac{1次以下}{2次式}}$$　が　$${\dfrac{f'(x)}{f(x)}}$$　のタイプではなかったときは　変形が必要となります

ここでの変形は　2つに分かれ
1つ目は　分母を因数分解　(部分分数分解のため)
2つ目は　分母を平方完成して特殊置換　(因数分解できなかったとき)
となります

まずは分母が因数分解できるときのお話です
基本的な部分分数分解の式がありましたので確認しましょう

3数の場合もありました　数列でも出てきたものですね

3数の場合にはここでは一般化はせず3連続整数の具体例だけにとどめます
後の恒等式の利用を考えればよいからです
ちなみに　数列では(＊)のところでストップしていました
なぜなら　数列での部分分数分解の目的は　項の相殺だったからです
しかし積分での目的は　積分可能な関数に分解することなので
そこからさらに分解します

そして　上の部分分数分解の公式は　いずれも分子が定数の場合に限ります

$${\dfrac{1次式}{2次式}}$$の場合には　その都度計算をするしかありません
部分分数分解の証明と同様の方法でうまく変形できますが
思いつかなかったり　分母が3次のときなどには
数学IIのところで学習した　恒等式を利用します

しかし　そもそもどういう形に分解できるのか　ということを知らないと恒等式が利用できません

いくつか代表的なものを列挙します
分母は$${(x+a)(x+b)}$$などとしていますが$${(ax+b)(cx+d)}$$等の場合でも大丈夫です
また大文字の$${AやB}$$は定数です

知らないと困るという　1つ具体例を紹介します

上の(＊)(＊＊)(＊＊＊)のうち，(＊)(＊＊)は間違っています
つまり，(＊)(＊＊)の形には分解することができないということです(定数$${a}$$や$${b}$$が存在しない)
一方　(＊＊＊)は正しいです($${a，b，c}$$が存在する$$)
正しいものの　積分を考えるとその後さらに分解することになります

したがって　上の例で紹介した通り

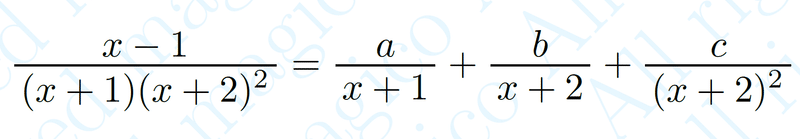
とおいて恒等式により$${a，b，c}$$を求めればよいです

特殊な置換積分の利用

前節の部分分数分解や恒等式の利用による分解は
分母が因数分解できる場合のお話でした
迷子になりそうなのでもう一度書きますが　変形は2つあり
1つ目は　分母を因数分解　(部分分数分解のため)
2つ目は　分母を平方完成して特殊置換　(因数分解できなかったとき)
です
問題では出てきていませんが次のような場合も1つ目です

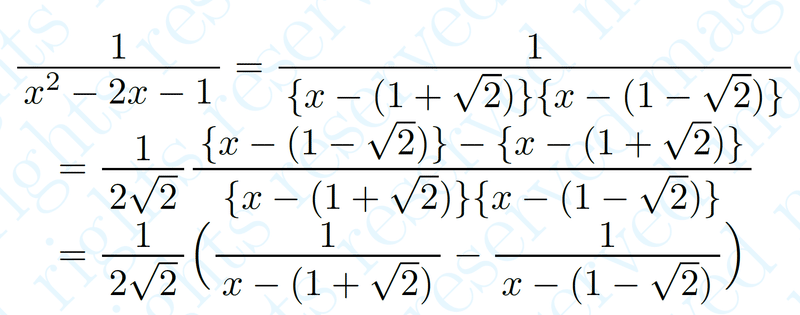
因数分解できるというのは　有理数の範囲ではなく実数の範囲です

そして2次式である分母が実数の範囲で因数分解できない場合には
平方完成によることとなります
この場合には定積分の問題となります

最後にまとめの1問です

ちょっと異なるだけで解法が分かれメンドウなところですね
真分数式化　$${\dfrac{f'(x)}{f(x)}$$かどうか　部分分数分解　特殊置換
という順序でしょうか
比較検討して理解しましょう