対象：定期試験以上

今回は　3次関数の概形　についてのお話です

関数$${f(x)}$$の形を決めるのは　導関数$${f'(x)}$$です
微分をして$${f'(x)}$$の正負の変化を考え増減表を書きますよね
もう少し強調していえば　$${f'(x)}$$のみで　$${f(x)}$$の概形が決まります

このように$${f'(x)}$$の正負の変化がわかれば　$${f(x)}$$の概形が決まるのですが
残念ながら　$${y}$$方向の位置　までは決まりません
この$${y}$$方向の位置は　$${f(x)}$$の定数項で決まります
積分のところで　積分定数$${C}$$が出てきますが　あれです

さて　極値があるかどうか　概形がどうなっているのか　は
$${f'(x)}$$を考えればわかるという話でしたが
次は　$${x}$$軸との交点　すなわち　$${f(x)=0}$$　の解との関係です

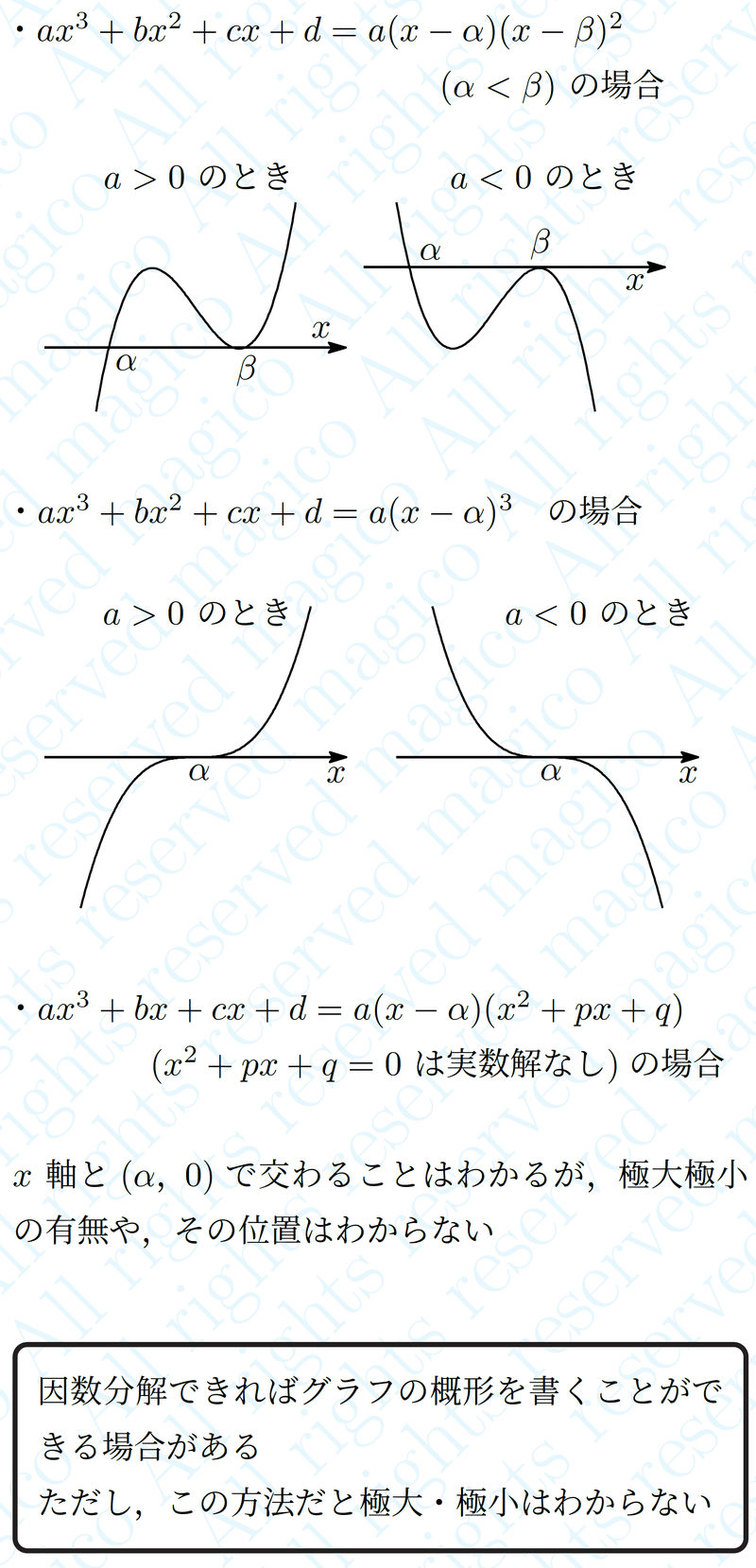
3次の係数$${a}$$の正負と　どのように因数分解できるのか　がわかると
やはり　概形が決まります(決まらない場合もある)
$${x}$$軸との交点の座標がわかれば　概形が決まるというのは
2次関数の場合と　同様ですね($${x}$$軸との交点がわかれば　平方完成せずともグラフがかけました)

ただ　因数分解を利用して概形を考えるときには
極値を与える$${x}$$の値がわからないんです(重解の場合にはわかる)
したがって　極大値極小値の問題ではなく
$${x}$$軸のとの交点が問題となる　3次不等式や定積分などで用います

以上　3次関数の概形　のお話でした