「三角関数」って何に使えるんですか?
こんにちは。ここでは身近に感じやすい理数(数学や物理)・言語(英語)系の記事を書いていこうと思っています。数学系の第2回目は数学の「三角関数」について書いてみます。
どうも三角関数は数学のつまずきやすいポイントになっているようでして、「三角関数が何の役に立つのかわからない」と思い、そのまま数学が苦手になってしまった人もいるかもしれません。ここでは数学の歴史と三角関数の現実的な意味について考えていきます。
もっとも、初めに断っておきますと、学問はそもそも、必ずしも実用性の追求を目的としていません。しかし、突き詰めた先で役に立つ例もあります。例えば虚数は一見何の役にも立ちそうにもありませんが、虚数を拡張して作られる複素数平面(ガウス平面)では二次元ベクトルの計算が簡単にできます。
とはいえ、数学の基礎的な項目のほとんどは必要があって作られてきたもので、三角関数もその例にもれません。そこで今回は、「三角関数は何に使えるのか」の質問に答えるために、そもそも「三角関数はなぜ世の中に出てきたのか」を説明しようと思います。
タレスによるピラミッドの高さの測量
三角関数の歴史は測量から始まります。
測量とは、物の高さや位置を角度を使って間接的に求める方法です。
その最も古い例の一つが、ソクラテス以前の古い時代、紀元前600年頃のエジプトの哲学者であるタレスです。
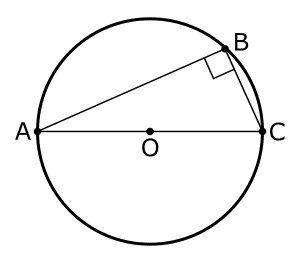
タレスの業績としてもっともよく知られるのは「タレスの定理」で、半円に内接する三角形は直角三角形であるというものです。上の図でいえば、角度Bが必ず90度になります。
ただ、ここでは「三角関数が何の役に立つのか」を説明したかったので、純粋数学の話はしません。測量におけるタレスの業歴を説明すると、それは「ピラミッドの高さを初めて求めたこと」です。
出典:Wikipedia:https://commons.wikimedia.org/wiki/File:Thales_Theorem_6.svg
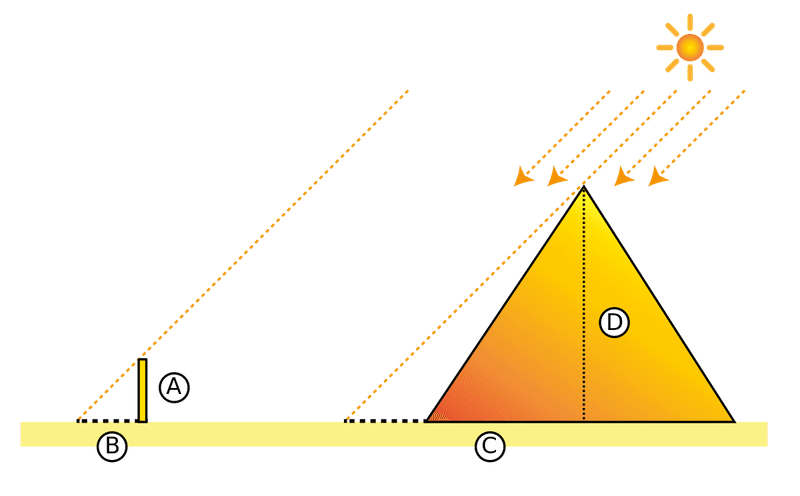
ある晴れの日、タレスはピラミッドの前へ行き、棒Aを地面にまっすぐに立てました。日が昇っていくと、やがて棒の影Bは短くなっていきます。そして、太陽が45°の角度となった時、太陽による影の棒が棒自身の長さと同じになります。このとき、タレスはピラミッドの影の長さCを測りました。このときの影の長さCこそが、ピラミッドの高さDであるわけです。
英語ですがわかりやすいサイトがありましたので、以下にリンクを貼っておきます。太陽の角度を自由に変えることができます。
三角測量
前述のタレスの方法はピラミッドとその影の長さが等しくなるまで、つまり太陽の角度が45度になるまで待ちました。しかし、そのうちに人類は、45度の角度でなくても、三角形の比の長さが分かれば計算できることに気づきます。そこで編み出されたのが三角測量です。
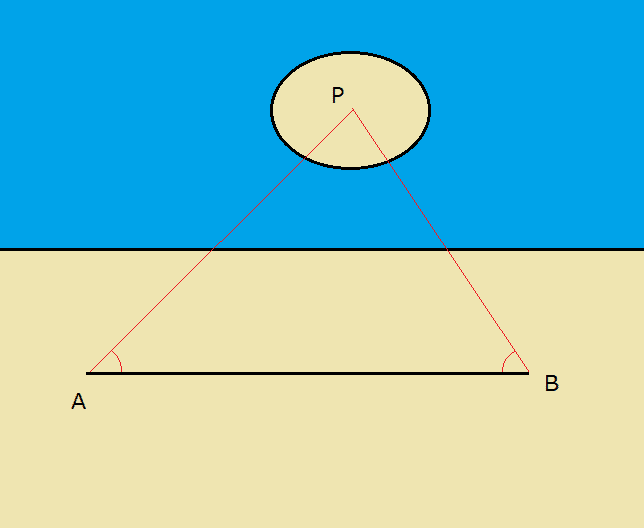
図では島の位置の測量を示している
三角測量とは、ある2地点A、Bの間の距離が明らかなとき、直接距離を測ることのできない点Cについて、地点A、Bからの角度によってその距離を求める方法です。
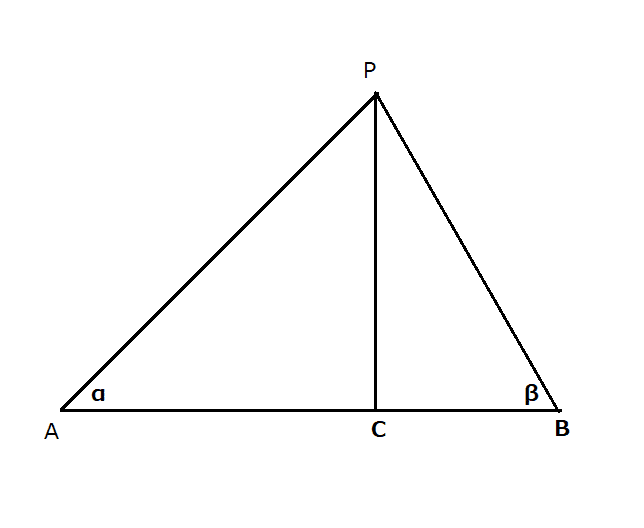
この時、線分ABを既知として点Pの位置を求められればよいわけです。ここで、点Pから線分ABに下した垂線の足をCとします。このとき、「三角比」を考えます。
直角三角形ACPを考えるとき、AC:CP=1:tanα
直角三角形BCPを考えるとき、BC:CP=1:tanβ
となりますから、
$${AB=AC+CB=\frac{CP}{\tan \alpha}+\frac{CP}{\tan \beta}=CP (\frac{1}{\tan \alpha}+\frac{1}{\tan \beta})}$$
$${\Leftrightarrow CP=\frac{AB}{(\frac{1}{\tan \alpha}+\frac{1}{\tan \beta})}=AB(\frac{\tan \alpha \tan \beta}{\tan \alpha+\tan \beta})}$$
としてCPの長さが計算できます。
CPの長さが分かれば、
$${AC=\frac{CP}{\tan \alpha}, CB=\frac{CP}{\tan \beta}}$$
ですから、ACとCBの距離もわかります。
よって、AからCの距離AC、BからCの距離BC、CからPの距離CPが分かるので、ABの距離と点Aと点Bからの角度αとβによって点Pの位置が求められたわけです。これが三角測量です。

三角測量はGPSによる測量が一般的ですが、三角測量も1980年代まで続けられましたので、太古の昔から2000年以上もの間、三角測量は実際に使われ続けてきたことになります。
月の距離の測量
三角測量は地上の測量にとどまりません。古代ギリシャの天文学者ヒッパルコスは月の距離の測定にも挑みました。
日食を使った方法
ヒッパルコスは、ヘレンポントスで同じ日に天頂上付近の日食を観測しました。そこでは皆既日食でしたが、子午線上にあって緯度が6°離れたアレクサンドリアでは5分の4の日食(つまり、5分の1だけずれた日食)でした。

太陽の視直径を0度30分(=0.5°)とすると、アレクサンドリアで見られる月の位置は、ヘレンポントスでの月の位置に対して0.5°×1/5=0.1°ズレていることになります。
月の視直径も0.5°ですから、言い換えれば、ヘレンポントスとアレクサンドリアは、地球の中心から見たときの角度は6°ずれていて、月から見たときの角度(上図のα)は0.1°ずれているということになります。

これを図で考えると、地球の中心をE、月をM、ヘレンポントスをB、アレクサンドリアをA、線分BAと線分MEの交点をCとすると、∠BEA=6°、∠HMA=0.1°となりますから、言い換えれば∠BEC=3°、∠BMC=0.05°となります。
ここから、EBに地球半径R、MBに地球と月の距離Lを用いると、
$${BC=EB\sin 3\degree=MB\sin 0.05 \degree}$$
$${\Leftrightarrow L=MB=EB \frac{\sin 3 \degree}{\sin 0.05 \degree}=R \frac{\sin 3 \degree}{\sin 0.05 \degree}\simeq 60R}$$
となります。
ヒッパルコスの計算では平均で地球半径の77倍という結果が出たようですが、当時としては高い精度であると言えます。
この日食を使った方法については以下のノートも詳しいです。
月食を使った方法
この方法は煩雑ですが、日食を使った計算よりもより正確にヒッパルコスは月までの距離を求めることができました。
結論から言うと、地球-月間の平均距離をLとしたとき、地球の半径をR、地上からの月の視半径の角度をθ、月の公転軌道における「地球の影」の視半径の角度をφとしたとき、
$${L=\frac{R}{\tan \theta + \tan \varphi}}$$
と計算できることを使って、地球-月間の平均距離は地球の半径の59倍であると結論付けました。
実際に地球と月の平均距離は約38万5000kmですから、地球半径6378kmに対して約60倍となるため、きわめて高い精度で計算していたことになります。
(※以下〈月食を用いる方法の説明〉の部分は数学的にハードで煩雑になりますので、答えを知りたいだけの人は飛ばしてもらっても構いません)
〈月食を用いる方法の説明〉
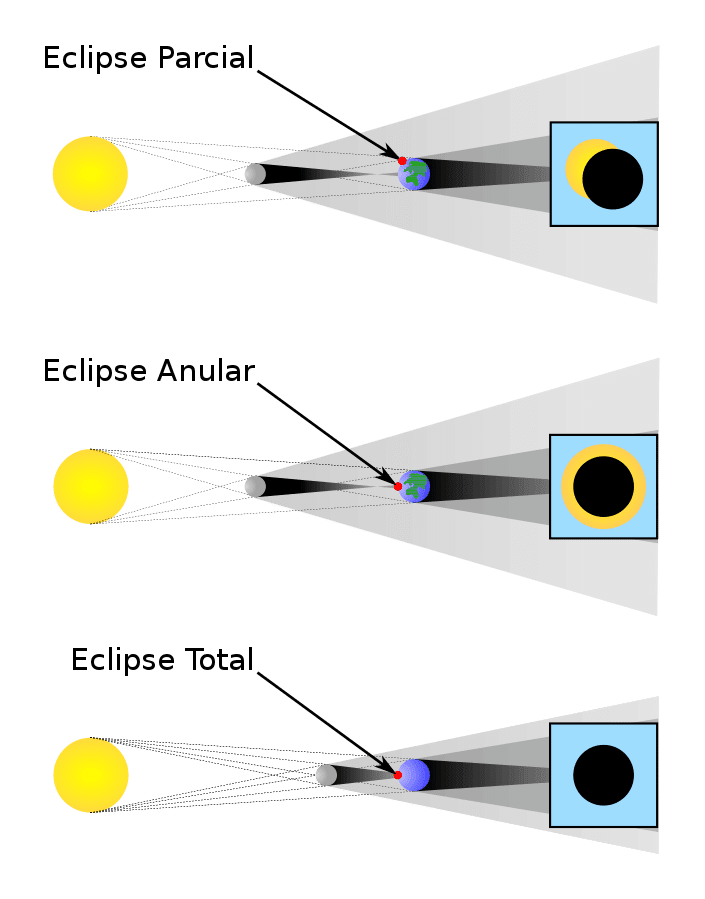
Wikipedia: https://commons.wikimedia.org/wiki/File:Solar_eclipse_3.svg より引用
太陽と月と地球の位置関係を考えます。皆さんは「皆既日食」や「金環日食」をご存じでしょうか。日食は月が太陽を覆うことで起こる現象ですが、月の大きさにより、皆既日食になったり金環日食になったりします。
言い換えると、地球から見たとき、月と太陽の見た目の直径はほぼ同じということです。
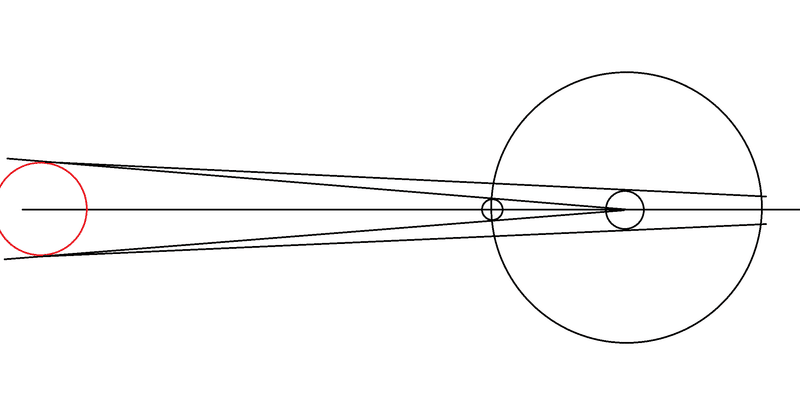
図で書くと上図のようになります。ここでは太陽が地球の近くに書いてありますが、実際ははるか遠方にあります。ここで、ヒッパルコスは太陽は地球より非常に遠い位置にあると考え、太陽は「無限遠方」にあると仮定しました。
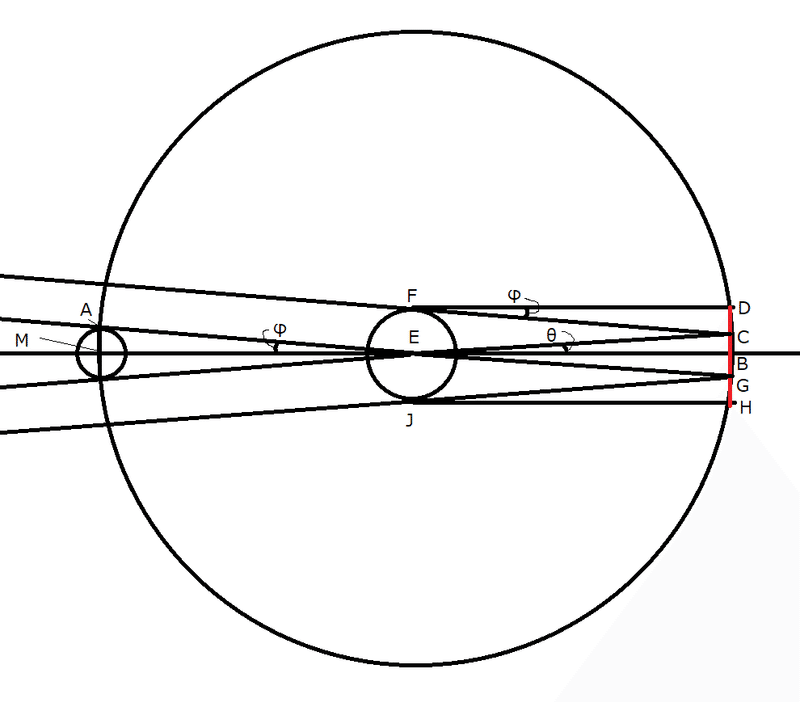
この時、距離MEと距離EBが地球-月間の距離を意味します。太陽は無限遠点にあるので、直線AEと直線FCは平行です。この時、月の公転軌道における地球の影の直径は線分CGに該当します。点C、点B、点Gは直線状にあると仮定します。
直線MEと平行になるように直線CG上に点Dを取って直線FDを考えれば、線分FDと線分BCの長さは等しくなります。点Hも同様に直線CG上に取ります。このとき、二つの角度(φと90°)とその間の長さ(FD=BC)が等しいので、⊿AMEと⊿CDFは合同になります。また、⊿CDFと⊿GHJも合同です。

ヒッパルコスの時代、月食の様子から、月の公転軌道における地球の影の径は、月の見た目の径のおよそ3倍程度であることが知られてしました。
月の半径をおよそ0.25°とすると、これをφとすると、月の公転軌道における地球の影の大きさの半径の角度θは、θ=3φ≒0.75°で表すことができます。
ここまでの情報をもとに、月までの距離ME(=Lとします)を求めてみます。月の半径MAをr、地球の半径EFをRとすると、
$${\tan \varphi = \frac{MA}{ME}=\frac{r}{L}...(1)}$$
また、
$${BC=\frac{1}{2}CG=\frac{1}{2}(DH-DC-GH)=\frac{1}{2}(2R-r-r)=R-r}$$
なので、
$${\tan \theta = \frac{BC}{EB}=\frac{BC}{L}=\frac{R-r}{L}...(2)}$$
(1)(2)から、
$${\tan \theta = \frac{R-r}{L}=\frac{R}{L}-\frac{r}{L}=\frac{R}{L}-\tan \varphi}$$
$${\Leftrightarrow \frac{R}{L}=\tan \theta+\tan \varphi}$$
$${\Leftrightarrow L=\frac{R}{\tan \theta+\tan \varphi}}$$
となります。
これを実際に計算すると、地球-月間の距離Lと地球の半径Rについて、
$${L=\frac{R}{\tan 0.75 \degree+\tan 0.25 \degree}\simeq \frac{R}{0.013091+0.004363}=57R}$$
となり、地球半径の57倍の距離という結果が得られます。ヒッパルコスが具体的にどのような数値を用いて計算したかは知られていないのですが、太陽を無限遠とした場合に地球半径の59倍という結果をヒッパルコスは得ているため、おそらく、月の視野の半径として、φ=14分30秒≒0.241666…度 を用いたと思われます、このとき、
$${L=\frac{R}{\tan 0\degree 43^\prime 30^{\prime\prime} +\tan 0\degree 14^\prime 30^{\prime\prime} }\simeq 59.2690R}$$
となり、ヒッパルコスの計算結果と合致します。
三角比から三角関数へ
測量において使用されたのはあくまで特定の角度の時の直角三角形の比であり、この時点ではまだ三角「関数」ではありませんでした。11世紀にはすでにアラビアのアル・ビールニー(973-1048)が正弦定理を導出していますし、余弦定理は紀元前のエウクレイデス(ユークリッド)の『原論』にその原形があり、16世紀に、前回の記事で文字式の考案者の一人として触れたフランスのヴィエトが余弦定理として確立しています。
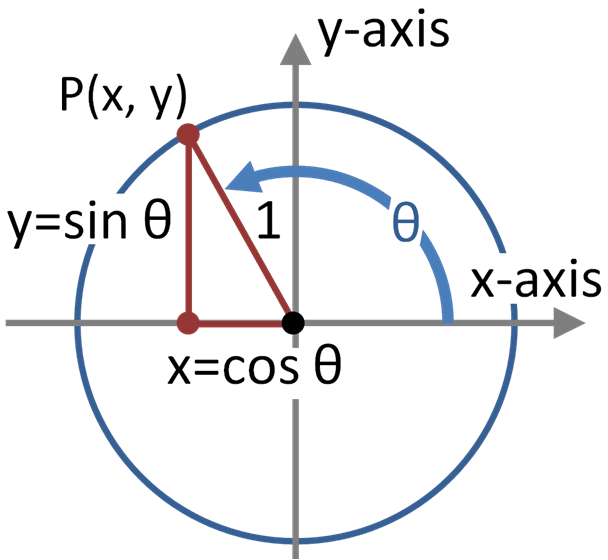
ルネサンス以降のヨーロッパでは三角比の研究が進みます。特に17世紀にデカルトがXY直交座標を考案すると、座標を用いれば三角比を鈍角、つまり角度が90度以上の場合にも三角比を拡張できることがわかります。これが「三角比の拡張」です。ここに、三角関数が生まれたといっても過言ではありません。
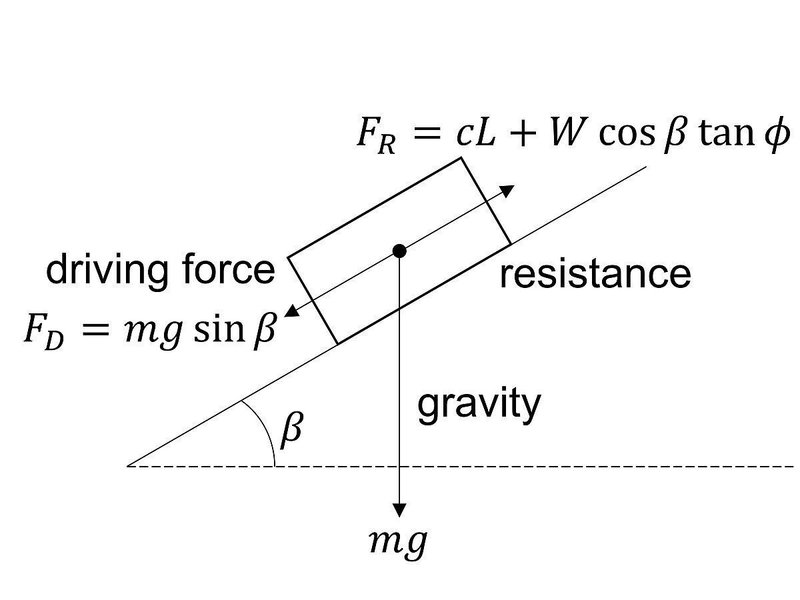
Wikipedia:https://commons.wikimedia.org/wiki/File:Mechanics_of_mass_movement.jpg より
物理学においても三角関数は応用されていきます。物理学習者はよくご存じでしょうが、高校数学で習うニュートン力学では三角関数によって「力の分解」を行います。これによって時間の関数として数式で物体の運動を計算す
ることができます。
表記法も徐々に現代のものに近づき、正弦をsine、余弦をco-sineと呼ぶようになり、17世紀になると、表記法もそれぞれsin、cosで定着していきます。
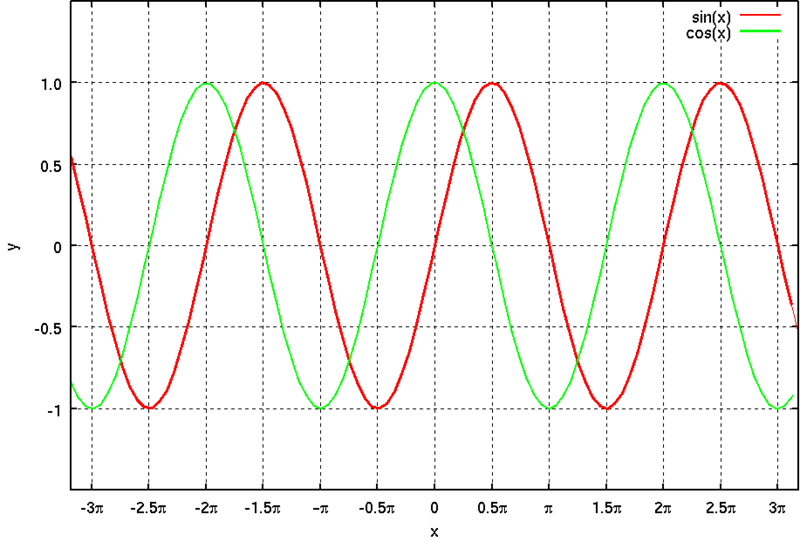
出典:Wikipedia https://commons.m.wikimedia.org/wiki/File:Sin_and_cos.png より
当初は三角比の表として数表でまとめられるのみでしたが、その後も研究が進み、ニュートンやスターリングにより数表の間の数値を計算するための「補完公式」が考案される中で「関数」としての理解が進みます。
最終的にオイラーにより「三角関数」として一般角に対して定義され、ついには虚数を含む数である複素数にまで拡張されることになります。例えば、sinθ=2 というのは高校数学では「解なし」ですが、大学数学では答えが出ます。ここでは説明はしませんが、三角関数はさらに拡張されていき、最終的には、指数関数と三角関数に関するオイラーの公式
$${e^{i \theta}=\cos \theta+i \sin \theta}$$
が発見されることになります。θにπを代入した公式は、「博士の愛した数式」でも紹介されたオイラーの等式
$${e^{i \pi}+1=0}$$
になります。
補足:プログラミングでの円の描写
プログラミングを実用例に入れるかどうか迷ったのですが、プログラミングも入れていいということであれば、円を描写するのに三角関数が必要です。プログラミングとは、人間の言葉と機械の言葉をつなぐ方法です。機械は人間の言葉を直接は理解できないのでプログラム言語を用いますが、プログラム言語とは数学そのものです。詳しく解説します。
そもそも円というのは、
$${x=x_0+R\sin \theta, y=y_0+R\cos \theta}$$
で示される点の軌跡のことです。
これを使った代表的なプログラムの例はアナログ時計の表示です。2022年現在はPythonが最も有名なプログラム言語なので、Pythonの例を紹介します。
このプログラムで三角関数がかかわる部分について解説します。
import math
### 定数
NEEDLE_H = 120 # 長針
NEEDLE_M = 160 # 短針
NEEDLE_S = 150 # 秒針
BASE_AGL = 90 # 基準角度
CENTER = int(WIDTH/2),int(HEIGHT/2)
(中略)
### 角度計算
angle_h = float(BASE_AGL - 30 * now.hour - 0.5 * now.minute) # 時
angle_m = int(BASE_AGL - 6 * now.minute) # 分
angle_s = int(BASE_AGL - 6 * now.second) # 秒
### 針の終端位置
pos_hx = round(math.cos(math.radians(angle_h))*NEEDLE_H) # 時のX座標
pos_hy = round(math.sin(math.radians(angle_h))*NEEDLE_H) # 時のY座標
pos_mx = round(math.cos(math.radians(angle_m))*NEEDLE_M) # 分のX座標
pos_my = round(math.sin(math.radians(angle_m))*NEEDLE_M) # 分のY座標
pos_sx = round(math.cos(math.radians(angle_s))*NEEDLE_S) # 秒のX座標
pos_sy = round(math.sin(math.radians(angle_s))*NEEDLE_S) # 秒のY座標
### 秒針表示
canvas.create_line(CENTER, CENTER[0]+pos_hx, CENTER[1]-pos_hy, width=8)
canvas.create_line(CENTER, CENTER[0]+pos_mx, CENTER[1]-pos_my, width=5)
canvas.create_line(CENTER, CENTER[0]+pos_sx, CENTER[1]-pos_sy, width=2)上記の角度計算はすべて度数法で指定されていますが、数学的には3時方向から逆時計周り(これがプラス方向)に角度を数えていくため、アナログ時計に合わせて、90度(12時方向)から時計周り(マイナス方向)に角度を指定します。数式で示すと、現在時刻tの時をh(t)、分をm(t)、秒をs(t)として、時針の角度をH(t)、分針の角度をM(t)、秒針の角度をS(t)とすれば、時計の針は、時針が1時間に30°かつ1分に0.5°進み、分針は1分に6°進み、秒針は1秒に6°進みますから、
$${H(t)=(90-30h(t)+0.5m(t))\degree}$$
$${M(t)=[90-6m(t)]\degree}$$
$${S(t)=[90-6s(t)]\degree}$$
となります。
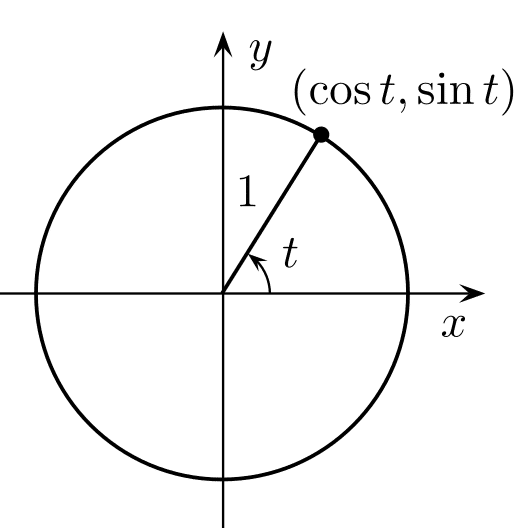
ここで時計の中心"CENTER"を(X0, Y0)と定義します(上のプログラムでは、正方形の画面"canvas"上の中央部分が指定されています)。この時の針の先の位置は、例えば時針では、時計の中心からの長さ"NEEDLE_H"を$$R_H$$とすれば、X座標をX(h)、Y座標をY(h)として、
$${X(h)=X_0+\cos (H(t))\degree \times R_H}$$
$${Y(h)=Y_0+\sin (H(t))\degree \times R_H}$$
と表記されます。中央の点と角度が分かれば、円上の点は三角関数で示すことができるからです。高校で勉強しましたね。分針、秒針の場合も同様です。
このように、プログラミングは数学ですから、三角関数は当然使われます。
まとめ
三角関数は、三角比として古代世界に現れ、「測量」のために使われ、特に三角測量は2000年以上の間、重要な測量の方法として使われ続けてきました。そこから発展して純粋数学においてもルネサンス以降に様々な定理が発見され、物理化学においても発展していきました。
数学的には三角関数は円上の任意の点を表せることから、プログラミングで円と角度の関係を示すときにも三角関数は使われています。
これを読んで三角関数が何に使えるのか、さらに何に発展できるのか、少しでも知ることはできたでしょうか? 興味のある人はぜひ三角関数の学習を進めてみてください。(記事終わり)
この記事が気に入ったらサポートをしてみませんか?
