７.3次方程式②

　一般の 3 次方程式 $${a_3x^3+a_2x^2+a_1x+a_0=0}$$ を考えるのですが，この 3 次方程式は $${x^3+px+q=0}$$ が解ければ十分であることが示せます。
　【注】$${a_3，a_2，a_1，a_0，p，q}$$ はいずれも実数です。
このとこは 3 次関数 $${y=a_3x^3+a_2x^2+a_1x+a_0}$$ のグラフがある点に関して対称になることと関係していますが，これはずっと後の話題なのでここでは割愛します。
とにかく $${x^3+px+q=0}$$ の型の 3 次方程式を解くとよいと飲み込んでください。

　多項式の方程式を解くとき，因数分解することは強力な方法の 1 つなのですが，ここでも因数分解を利用します。
まず，$${a^3+b^3+c^3-3abc}$$ を因数分解しましょう。
$${(a+b)^3=a^3+3a^2b+3ab^2+b^3=a^3+b^3+3ab(a+b)}$$ なので
$${a^3+b^3=(a+b)^3-3ab(a+b)}$$ となります。
よって，

$$
\begin{align*}
a^3+b^3+c^3-3abc &=(a+b)^3-3ab(a+b)+c^3-3abc\\
&=(a+b)^3+c^3-3ab(a+b)-3abc\\
&=(a+b)^3+c^3-3ab(a+b+c)
\end{align*}
$$

です。
ここで $${x^3+y^3=(x+y)(x^2-xy+y^2)}$$ であることから，
$${x=a+b，y=c}$$ とすれば

$$
\begin{align*}
(a+b)^3+c^3 &=\{(a+b)+c\}\{(a+b)^2-(a+b)c+c^2\}\\
&=(a+b+c)(a^2+b^2+c^2+2ab-bc-ca)
\end{align*}
$$

となるので

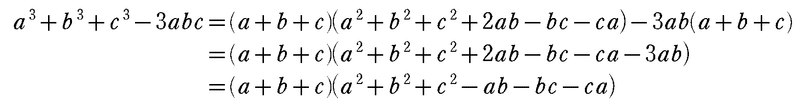
と因数分解できました。

　この因数分解が利用できるように $${x=u+v}$$ とおきます。
すると　$${x^3=(u+v)^3}$$
　　　　$${x^3=u^3+3u^2v+3uv^2+v^3}$$
　　　　$${x^3=u^3+v^3+3uv(u+v)}$$
であり，$${u+v=x}$$ であることに注意して整理すると

$$
x^3-3uvx-u^3-v^3=0
$$

となります。この式と $${x^3+px+q=0}$$ を比べると

$$
p=-3uv，q=-u^3-v^3
$$

であることがわかります。これは後で使う式なので覚えておいてください。

 さて，$${x^3-3uvx-u^3-v^3}$$ に $${a^3+b^3+c^3-3abc}$$ の因数分解を適用するために $${a=x，b=-u，c=-v}$$ と置き換えます。
　$${x^3-3uvx-u^3-v^3=x^3+(-u)^3+(-v)^3-3×x×(-u)×(-v)}$$
ですから

$${(x-u-v)\{x^2+(-u)^2+(-v)^2-x×(-u)-(-u)×(-v)-(-v)×x\}}$$
$${=(x-u-v)(x^2+u^2+v^2+ux-uv+vx)}$$
$${=(x-u-v)\{x^2+(u+v)x+u^2-uv+v^2\}}$$

となります。よって，$${x^3-3uvx-u^3-v^3=0}$$ のとき
$${x-u-v=0}$$ より $${x=u+v}$$（注：これは当然の結果です）
$${x^2+(u+v)x+u^2-uv+v^2=0}$$ は 2 次方程式の解の公式から

$$
\begin{align*}
x &=\cfrac{-(u+v)±\sqrt{(u+v)^2-4(u^2-uv+v^2)}}{2}\\
&=\cfrac{-(u+v)±\sqrt{u^2+2uv+v^2-4u^2+4uv-4v^2}}{2}\\
&=\cfrac{-(u+v)±\sqrt{-3(u-v)^2}}{2}\\
&=\cfrac{-(u+v)±\sqrt{(u-v)^2}\sqrt{3}i}{2}
\end{align*}
$$

となります。
ここで，$${u-v≧0}$$ なら $${\sqrt{(u-v)^2}=u-v}$$，
　　　　$${u-v<0}$$ なら $${\sqrt{(u-v)^2}=-(u-v)}$$
ですが，
$${\sqrt{(u-v)^2}}$$ の前が $${±}$$ なので，符号は気にする必要がなく，
　　$${x=\cfrac{-(u+v)±(u-v)\sqrt{3}i}{2}}$$
とできます。

【注】$${u-v}$$ が虚数の場合も $${(u-v)^2}$$ か $${\{-(u-v)\}^2}$$ かの問題がありますが，実数の場合と同じ理由で，符号は気にする必要がありません。

さらに $${u，v}$$ の係数がはっきりするように変形すると
　　$${x=\cfrac{-1±\sqrt{3}i}{2}u+\cfrac{-1∓\sqrt{3}i}{2}v}$$（複合同順）…（＊）
です。
ここで，$${ω=\cfrac{-1+\sqrt{3}i}{2}}$$ のとき $${ω^2=\cfrac{-1-\sqrt{3}i}{2}}$$ であったことを思い出してください。

【参考】$${ω}$$ は $${x^3=1}$$ の虚数解です。

これを使うと（＊）は $${x=ωu+ω^2v，ω^2u+ωv}$$ と書くことができます。
まとめると，$${x^3-3uvx-u^3-v^3=0}$$ の解は
　$${x=u+v，ωu+ω^2v，ω^2u+ωv}$$
であると求められます。

　この解はもう少しコンパクトに書くことができます。
$${ω}$$ は 3 次方程式 $${x^3=1}$$ の虚数解なので $${ω^3=1}$$ であり，$${ω^0=1}$$ であることを利用すると

$$
x=ω^ku+ω^{3-k}v（k=3，2，1）
$$

となります。
この $${k}$$ を用いた式で
　$${k=3}$$ とすれば $${x=u+v}$$
　$${k=2}$$ とすれば $${x=ω^2u+ωv}$$
　$${k=1}$$ とすれば $${x=ωu+ω^2v}$$
が得られるからです。

　　そして，いよいよ最終段階として $${p，q}$$ と $${u，v}$$ の関係を
$${p=-3uv，q=-u^3-v^3}$$ から導きます。
まず，$${u^3=X，v^3=Y}$$ とおきます。$${u=\sqrt[3]{X}，v=\sqrt[3]{Y}}$$ となります。

【注】ここでは，3 乗して $${X，Y}$$ になる数を $${\sqrt[3]{X}，\sqrt[3]{Y}}$$ と書くことにします。

すると，$${p^3=-27u^3v^3=-27XY}$$ より $${XY=-\cfrac{p^3}{27}=-\left(\cfrac{p}{3}\right)^3}$$ であり
$${q=-X-Y}$$ より $${X+Y=-q}$$
となります。
ここで，$${X，Y}$$ を解とする $${t}$$ に関する 2 次方程式の 1 つは
$${(t-X)(t-Y)=0}$$ より $${t^2-(X+Y)t+XY=0}$$ となるので，$${X，Y}$$ は
2 次方程式 $${t^2+qt-\left(\cfrac{p}{3}\right)^3=0}$$ の解ということになります。
よって，2 次方程式の解の公式を使うと

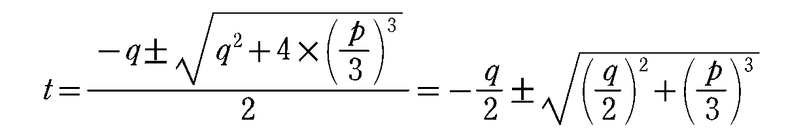
なので，$${X}$$，$${Y}$$ は解の中央の $${+}$$ をとったものか $${-}$$ をとったものかのどちらかです。ところで，$${X+Y}$$ と $${XY}$$ は $${X，Y}$$ について対称な式（$${X，Y}$$ の役割を入れ替えても式の値が変わらない式）になっているので

としても一般性は失われません。
したがって，$${u=\sqrt[3]{X}，v=\sqrt[3]{Y}}$$ から

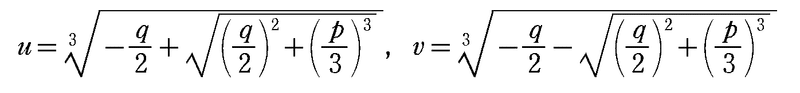
となります。

　よって，3 次方程式 $${x^3+px+q=0}$$ の解は，$${x^3=1}$$ の虚数解 $${ω}$$ を用いて

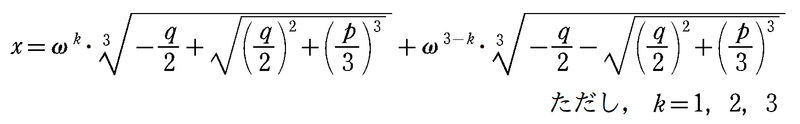
となります。これが 3 次方程式の解の公式です。

【参考】4 次方程式にも解の公式が存在しますが，それを解く過程で 3 次方程式の解の公式が利用されます。5 次方程式以上の高次の方程式には解の公式が存在しないことが証明されていますが，高校数学の範囲をはるかに超える内容です。

練習問題　3 次方程式 $${x^3-15x-4=0}$$ を解け。
　[ヒント]：$${\sqrt[3]{2±11i}=2±i}$$（複合同順）です。

【答】$${x=4，-2±\sqrt{3}}$$