３．1 次関数のグラフ

 有理数と無理数を方程式編で説明しましたが，これらの数を合わせて実数という数の集まりができます。そして，実数は数直線上の点の位置で表現できる数です。
整数は，数直線上に定規の目盛りと同じように等間隔に目盛りをつけ，その目盛りに 0 より右側には正の整数，左側には負の整数を対応づけして表現できます。小学校の頃にも数直線を描くことがあったはずです。

そして，$${\cfrac{整数}{整数}}$$ と書くことができる整数を拡張した数である有理数は，この数直線上の整数と整数の間をさらに等間隔に目盛ることで表現できます。
たとえば $${\cfrac{9}{10}}$$ は，0 と 1 の間を 10 等分して左から順に

$$
\cfrac{1}{10}，\cfrac{2}{10}，\cfrac{3}{10}，・・・，\cfrac{9}{10}
$$

のように目盛ることで表現され，$${\cfrac{6}{5}}$$ なら 1 と 2 の間を 5 等分して 1 のすぐ右の目盛りで表現されます。
（0 と 1 を 5 等分したときの 1 は $${\cfrac{5}{5}}$$ です。）
それでは，無理数はどのように目盛れるでしょうか。
例えば $${\sqrt{2}}$$ は無理数ですが，それを目盛るには一辺の長さが 1 の正方形の対角線と同じ長さのヒモを用意します。するとそのヒモの長さが $${\sqrt{2}}$$ となります。そして，そのヒモの左端を数直線の基準点 $${\mathrm{O}}$$（実数の 0 に対応する点）にあてて，それがたるまないように数直線上に置いたときの右端の位置で $${\sqrt{2}}$$ が目盛れます。

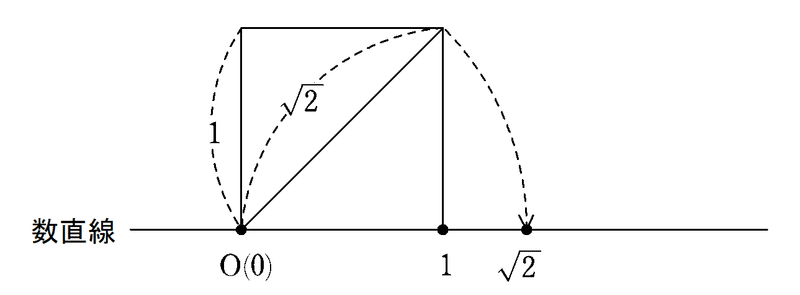
有理数を数直線上で目盛ることは直感的にわかりやすいですが，それとは対照的に，無理数を数直線上で目盛ることは，上述の通りなかなかやっかいです。
しかし，どんな異なる二つの有理数の間にも必ず無理数を見出すことが示せます。残念ながらこのことを説明するには，中学数学の守備範囲を大きく超えなければなりません。ですから今後は，数直線上のどこに目盛りをつけても，必ずそれに対応する実数が見出せると飲み込んでください。

　ところで，本題とは少しずれますが，一辺の長さが 1 の正方形の対角線の長さが $${\sqrt{2}}$$ となることを説明しておきます。

図の様な正方形 $${\mathrm{ABCD}}$$ において△$${\mathrm{ABC}}$$ は正方形 $${\mathrm{ABCD}}$$ を半分にした三角形なので，その面積は

$$
1×1×\cfrac{1}{2}=\cfrac{1}{2}
$$

となります。
正方形の対角線は長さが等しく各々の中点で垂直に交わるので，その点を $${\mathrm{H}}$$ としたとき $${\mathrm{BH}=\cfrac{1}{2}\mathrm{AC}}$$ であり，$${\mathrm{AC}⊥\mathrm{BH}}$$ です。
いま $${\mathrm{AC}=x}$$ とおくと △$${\mathrm{ABC}}$$ の面積は

$$
\cfrac{1}{2}×\mathrm{AC}×\mathrm{BH}=\cfrac{1}{4}x^2
$$

となります。
したがって，$${\cfrac{1}{4}x^2=\cfrac{1}{2}}$$
　　$${x^2=2}$$
　　$${x=±\sqrt{2}}$$
です。
もちろん，$${x>0}$$ ですから $${x=\mathrm{AC}=\sqrt{2}}$$ となります。
説明は終わり。

　次に平面上の点の位置について，どう表現できるのか見てみましょう。
今度は一つの直線上だけでなく，縦と横の面上の広がりをもった中での点の位置になります。それにはまず，基準点 $${\mathrm{O}}$$（実数の 0 に対応する点）を通る，2 本の直交する直線を引きます。この直交する 2 つの直線でつくられる平面が座標平面です。この座標平面上で，ある点の位置を表すには，横軸上での値と，縦軸上での値の 2 つの値を与えて指定します。そして 2 つの値を

(横軸の値，縦軸の値)

のように，カッコの中でカンマで区切って書き表します。
それでは，具体的に $${(3，5)}$$ の点の位置を指定してみましょう。横の数直線上（普通，水平に引いた直線で，これを $${x}$$ 軸といい右向きを正とします。）で，実数 $${3}$$ を目盛り，縦の数直線上（先の $${x}$$ 軸に垂直に引いた直線で，これを $${y}$$ 軸といい上向きを正とします。）で，実数 $${5}$$ を目盛ります。そして，それぞれの実数から，互いの軸に平行に線を引いて，その交わったところが点 $${(3，5)}$$ の位置となります。

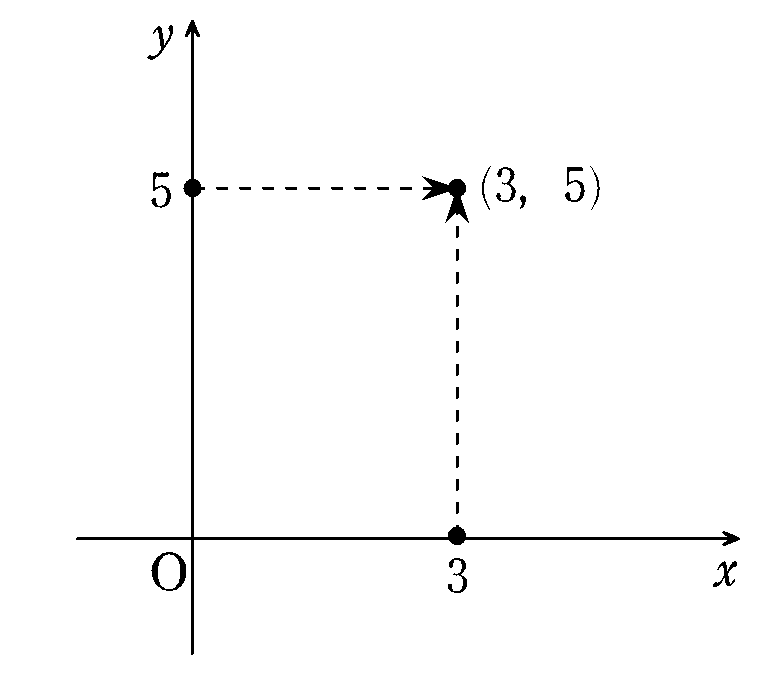
一般に，座標平面上に点 $${\mathrm{A}}$$ $${(a，b)}$$ と与えたとき，$${a}$$ を点 $${\mathrm{A}}$$ の $${x}$$ 座標，$${b}$$ を点$${\mathrm{A}}$$ の $${y}$$ 座標といいます。

　それでは，$${x}$$ についての 1 次関数である $${y=2x}$$ を座標平面上で表すことを考えてみましょう。
（$${y=2x}$$ を座標平面上であらわしたものを，$${y=2x}$$ のグラフといいます。）
まず，$${y=2x}$$ の $${x}$$ に具体的な数値を代入して，それに対応する $${y}$$ の値を表に書いてみます。

この表の $${x}$$，$${y}$$ を点 $${(x，y)}$$ として座標平面上にとってみると下の図１のようになります。

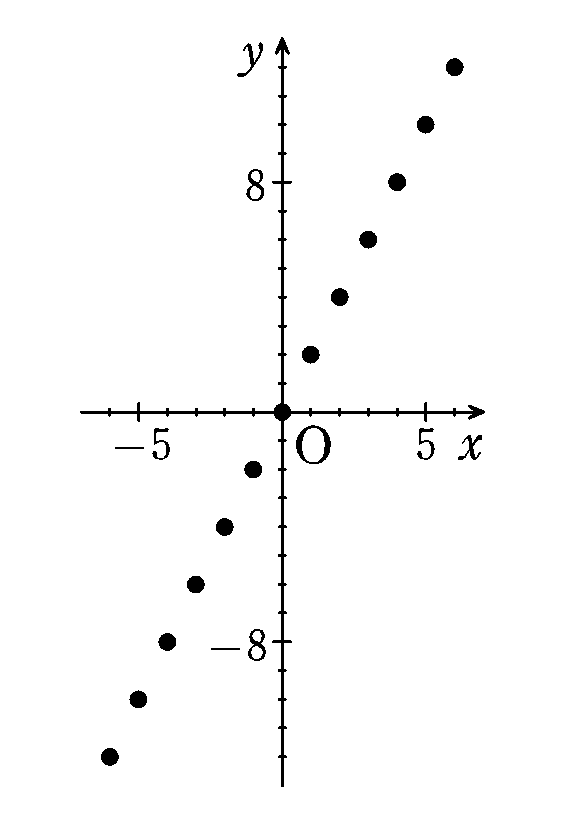
そして，これらの点の間を $${y=2x}$$ を満たす点 $${(x，y)}$$ で埋めていくと図２のようになり，1 次関数 $${y=2x}$$ のグラフの完成です。

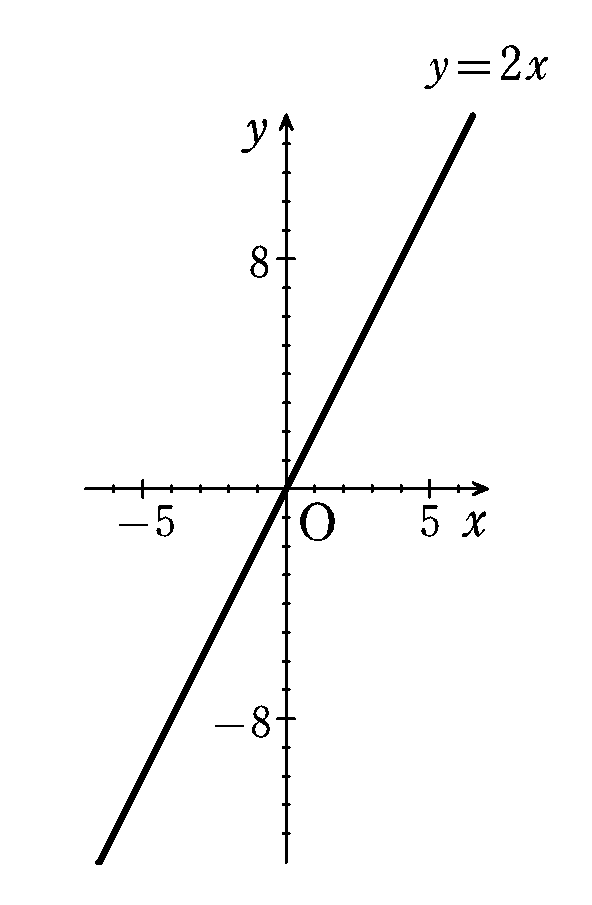
　一般に，$${y=ax}$$ のグラフは原点を通る直線となり，$${a}$$ をこの直線の傾きといいます。そしてグラフは，$${a>0}$$ のときは右上がりの，$${a<0}$$ のときは右下がりの直線になります。

　それでは，いよいよ 1 次関数 $${y=ax+b}$$ のグラフの番です。
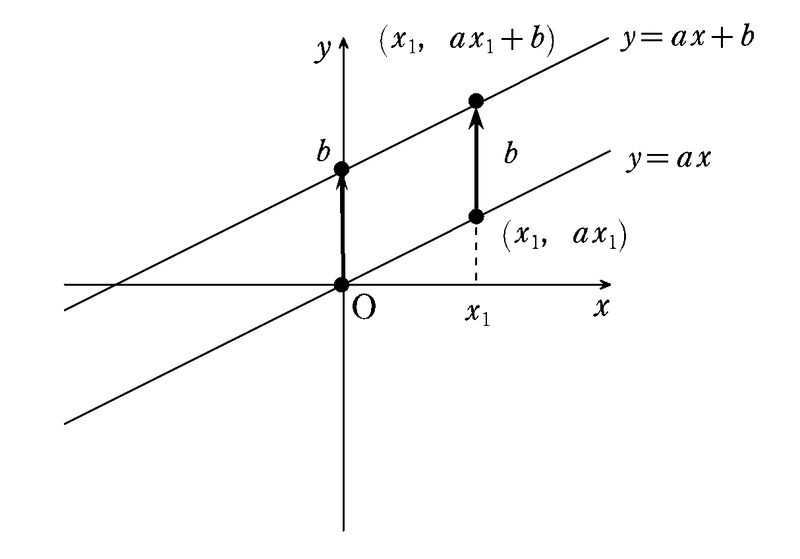
$${y=ax}$$ のグラフは原点を通る直線になるでしたが，この直線上に点 $${(x_1，ax_1)}$$ をとります。そして，この点を $${y}$$ 軸に平行に $${b}$$ だけ移動させます。このことを点 $${(x_1，ax_1)}$$ を $${y}$$ 軸方向に $${b}$$ だけ平行移動する，といいます。この移動させた点の座標は $${(x_1，ax_1+b)}$$ となり，これが $${y=ax+b}$$ のグラフ上にあることは $${y=ax+b}$$ で $${x=x_1}$$ とすると $${y=ax_1+b}$$ となることから明らかです。
ところで，$${x_1}$$ は任意にとれるので，結局 $${y=ax+b}$$ のグラフは $${y=ax}$$ のグラフを $${b}$$ だけ引き上げた（$${b<0}$$ なら引き下げた）ものになります。このことを $${y=ax+b}$$ のグラフは $${y=ax}$$ のグラフを $${y}$$ 軸方向に $${b}$$ だけ平行移動したものである，といいます。また，$${y=ax}$$ 上の点である原点 $${(0，0)}$$ は平行移動によって $${y=ax+b}$$ のグラフ上の点 $${(0，b)}$$ に移動しますが，この $${b}$$ をグラフの切片といいます( $${y}$$ 切片ともいう)。まとめると $${y=ax+b}$$ のグラフは傾きが $${a}$$，切片が $${b}$$ の直線である，となります。

練習問題　1 次関数 $${y=-\cfrac{1}{2}x+3}$$ のグラフの傾き，切片を言え。

【答】傾きは $${-\cfrac{1}{2}}$$，切片は $${3}$$