
仮説検定を学ぶ
この章の目的
人間社会の活動によって出現し複雑に変動する事象は、運動方程式を計算して出てくる答えのように精密な予測をすることはできません.
しかし推測統計学という強力な技術の蓄積のおかげで事象の背後にある母集団の特徴を理解する道が開かれています.
この章では後続の時系列分析や機械学習に取り組むために必要となる統計学の知識を確認していこうと思います.特に確率の道具立てのところは,あれってどうなってたかな?と振り返ることがよくあるので補足資料もつくって情報の整理を厚くしたつもりです.
1. 母集団とは何ですか?
本稿が想定する「母集団(Population)」は、物理や工学の世界と同じく調査や実験を通じて答えを得ることができる対象です.ただし自然現象のように根本がランダムな事象というよりも集団の要素の数が相当に大きくなおかつ観測や調査方法の制約のためランダム性があるように扱うことができる、という類の対象を考えています.
一般に母集団の要素の数が膨大になれば調査や実験の対象を一定数以下に限定せざるを得ません.この限定の仕方に人為的,作為的な偏りが生じないように抽出された部分集団のことを無作為抽出標本(以下では簡単に「標本」)と呼びます.標本のとりうる値全体が「標本空間」です.そして標本を得るための調査や実験のことを本稿では「試行」と呼ぶことにします.
母集団からn個の要素を観測する試行があったとしましょう.その要素が示す量が実数だとすれば標本空間は$${ \R^n}$$です.試行対象の要素のとりうる値はひとつの分布にしたがうという前提をおき,これを「母集団分布」といいます.「ひとつの分布」とわざわざいう理由は,観測対象の要素が二つの変量をもっている場合,二変量を規定する分布がひとつ存在している,という考え方をするからです.
母集団の特徴を要約した定量的数値が「母数(Modulus)」です.あるいは一般に母集団の特徴を決める量として「母集団のパラメータ」という言葉もよく使われます.母集団分布の平均や分散は代表的な母数です.そして標本に対しても同様に特徴を要約した定量的数値を考えることができ,これを「統計量(Statistic)」といいます.
1.1. 確率変数
標本の無作為性は標本,さらには標本を集めた集合である標本空間Ωの部分集合の出現確率によって特徴づけられます.出現確率が定義された標本空間の部分集合のことを「事象(Event)」といいます.標本は根源事象と呼ばれることもあります.「確率変数(Random variable)」とは根源事象(標本)に対してその出現確率を対応づけた関数のことです.統計量を母集団分布に従う確率変数として扱うことには確率論の様々な知識を活用できるメリットがあります.
標本は独立同分布の確率変数の列$${X = (X_1,X_2,..,X_n )}$$であるとします.このため試行により実際に得られた値$${( x_1,x_2,..,x_n )}$$を標本とは区別する意味でXの「実現値」とか「観測データ」と呼ぶことがあります.標本の算術平均(以後標本平均あるいは単に平均と呼ぶ)$${\quad \overline{X}=(X_1+X_2+..+X_n)/n \quad}$$は統計量であり,$${\quad \overline{x}=(x_1+x_2+..+x_n)/n \quad}$$は$${\overline{X}}$$の実現値です.一般に母数や母集団の特徴を決めるパラメータを直接計測することは困難です.なので,正しいと思われる「統計モデル」をもとに統計量からそれらの値を推定する試みが仮説検定の大きな目的であると言えます.統計モデルという用語は時系列分析や機械学習への応用では「予測モデル」と言われることもあるようです.
(注)
ここでは標本という言葉から始めて次に確率変数を持ち出しましたが、現代的な確率の定義では、出現確率Pを定義できる事象の集まり$${\mathscr{F}}$$と根源事象の集まり$${ \Omega}$$を考え三点セット{$${\Omega,\mathscr{F},P}$$}を確率空間とよぶところからスタートします.そしてその空間の上で確率変数の概念を定義する流れになっています.ではあるのですが確率変数という言葉から浮かぶ常識的なイメージ,つまり「観測するたびに不規則に値が変動する量」という理解でも本稿ではあまり問題なさそうなので数学的に精密な説明は省きます.しっかりした説明を知りたい場合は確率論に関する教科書・文献は数多くあるので参照ください.参考書をここではひとつだけ「参考1」をあげておきました.確率の意味からはじまってファイナンス数理まで適度なページ数に収まっていて読み物としてもてうれしい.
一変量の確率変数
確率変数Xが離散的な場合(例えばサイコロの目の数),値xをとる確率を関数として定めることで確率変数の性質は決まります.この関数を$${f_X}$$と書き「確率関数(あるいは確率質量関数,probability mass function,pmf)」と呼びます.Xが従う「確率分布」は確率関数により以下のように表現できます.
$$
\begin{aligned}
P(a \le X \le b) = \sum_{a \le x \le b}f _ X(x)
\end{aligned}
$$
なお$${\hspace{0.2em} P(X \le b)\hspace{0.2em}}$$,つまりXがb以下のとなる確率を慣習的に「(累積)確率分布関数(cumulative cistribution function , cdf)」と呼ぶことが多いので少し紛らわしい感じがしますね.
累積分布関数の逆関数、つまり確率 pを与えたときに, $${\hspace{0.2em} P(X \le b)\hspace{0.2em}=p}$$ となる確率変数の値 b を返す関数のことをパーセントポイント関数(the Percent-Point Function,ppf)と呼びます.この関数は分位関数(quantile function)あるいは逆累積分布関数(inverse cumulative distribution function,icdf)とも呼ばれ統計分析では頻出するようです. 分位数については「補足説明 分位数」にも少しまとめておきました.
一方,連続的な確率変数X(例えば身長や体重)に対しては,一点の出現確率はゼロになってしまうので代わりに区間の確率を積分形式で定めることで確率変数の性質は決まります.この被積分関数を$${f_X}$$と書き「確率密度関数( probability density function , pdf)」と呼びます.確率密度関数を使うと,Xが従う「確率分布」は以下のように表現できます.
$$
\begin{aligned}
P(a \le X \le b) = \int_a^bf_X(\omega)d\omega
\end{aligned}
$$
多変量の確率変数
サイコロとコインを同時に複数回投げる試行のように,標本の各要素を種類の異なる確率変数からなるベクトルとみなしたい場合があります.その場合標本の要素$${\mathbb{X_t}= ( X_{1t},..,X_{nt} )}$$の「同時確率」(複数の変数の値を同時に決める意味で同時確率という)を与える確率質量関数$${f_X(x_1,..,x_n)}$$によって性質は決まります.以後標本要素を区別する添え字は誤解の恐れが少ない場合は省略します.$${\mathbb{X}}$$が従う確率分布は,
$${A = A_1 \times..\times A_n:=\lbrace (a_1,..,a_n) \mid a_1 \in A_1,..,a_N \in A_n \rbrace}$$
を事象とすると以下のように表されます.
$$
\begin{aligned}
P(\mathbb{X} \in A) = \sum_{ x _ 1 \in A _ 1}...\sum_{x _ n \in A_ n }f _ X( x _ 1,..,x _ n) \end{aligned}
$$
なお以後$${\lbrace \mathbb{X} \in A \rbrace}$$を$${\lbrace X_{1} \in A_1,..,X_{n} \in A_n \rbrace}$$のように表すこともあります.
一つの変数$${X_i}$$のみの確率分布をみるために他の変数について総和することを周辺化と呼び,その結果の分布を$${ X_i }$$の「周辺分布」と呼びます.
$$
\begin{aligned}
P(X_1 \in A_1) = \sum_{x_1 \in A_1}\sum_{x_2 \in \R}..\sum_{x_n \in \R}f_X(x_1,..,x_n)
\end{aligned}
$$
工場ラインを流れる部品のサイズと重量を測定する試行のように標本要素が連続値の確率変数となる場合は,標本要素$${\mathbb{X_t}= ( X_1,...,X_n )}$$の同時確率密度関数$${f_X(x_1,..,x_n)}$$によって性質は決まります.$${\mathbb{X_t}}$$が従う確率分布は,Aを事象とすると以下のように表されます.
$$
\begin{aligned}
P(\mathbb{X} \in A) = \int_{x_1 \in A_1}..\int_{x_n \in A_n}f_X(x_1,..,x_n)dx_1..dx_n
\end{aligned}
$$
離散変数と同様周辺化,周辺分布を定義します.
$$
\begin{aligned}
P(X_1 \in A_1) = \int_{x_1 \in A_1}\iint_{\R \times .. \times \R}f_X(x_1,..,x_n)dx_1..dx_n \end{aligned}
$$
条件付確率
確率変数X,確率変数Yとするとき,$${Y \in B}$$のもとで$${X \in A}$$となる「条件付確率」は (同時確率 ÷ 周辺確率)として定義されます.
$$
\begin{aligned}
P( X \in A | Y \in B) \hspace{0.5em} := \hspace{0.5em} \frac { P(X \in A , Y \in B)} {P(Y \in B)}
\end{aligned}
$$
確率変数に関する基本的な定義
確率変数に対しては頻出する重要な量がいくつかあるので以下に定義を書いておきます.
(注)$${\hspace{0.3em}\coloneqq \hspace{0.3em}}$$は定義を意味する等号ですが,以降誤解の恐れがない場合には普通の等号を使う場合もあります.
【一変量確率変数】
確率変数 X は平均 $${\mu}$$ の確率分布 P に従うとします.
$$
\begin{aligned}
\text{期待値} E(X) & \coloneqq \sum_{x\in R:P(x)>0}P(x) \text{離散確率変数の場合} \newline
\text{分散} V(X) & \coloneqq E((X-\mu)^2) \coloneqq \sum_{x\in R:P(x)>0}(x-\mu)^2P(x) \text{離散確率変数の場合} \newline
\text{期待値} E(X) & \coloneqq \int_{-\infty}^{+\infty}xf_X(x)dx \text{連続確率変数の場合} \newline
\text{分散} V(X) & \coloneqq E((X-\mu)^2) \coloneqq \int_{-\infty}^{+\infty}(x-\mu)^2f_{X}(x)dx \text{連続確率変数の場合} \newline
\end{aligned}
$$
【多変量確率変数】
変量数が2以上の場合の定義も同様なので二変量の場合を記述します.
確率変数のペア$${\mathbb{X} = (X,Y)}$$の各要素は平均 $${(\mu_X,\mu_Y)}$$ の同時確率分布 P に従うとします.
$$
\begin{aligned}
\text{期待値ベクトル} E(\mathbb{X}) &\coloneqq (E(X),E(Y))^T \newline
\text{分散ベクトル} V(\mathbb{X}) &\coloneqq (V(X),V(Y))^T \newline
\text{共分散行列} Cov(\mathbb{X},\mathbb{Y}) & \coloneqq E((X-\mu _ X)(Y-\mu _ Y)) \newline
& \coloneqq \begin{pmatrix}
V(X) & Cov(X,Y) \newline
Cov(Y,X) & V(Y)
\end{pmatrix} \newline
\text{相関係数} \rho_{XY} & \coloneqq \frac{Cov(X,Y)}{\sqrt{V(X)}\sqrt{V(Y)}} \newline
Cov(X,Y)\text{(離散型の共分散):} \newline
Cov(X,Y) & \coloneqq \sum_{x\in R:P(x)>0}\sum_{y\in R:P(y)>0}(x-\mu_X)(y-\mu_Y)P(x,y) \newline
Cov(X,Y)\text{(連続型の共分散):} \newline:
Cov(X,Y) & \coloneqq \iint_{-\infty}^{+\infty}(x-\mu_X)(y-\mu_Y)f_{XY}(x,y)dxdy
\end{aligned}
$$
確率変数 X,Y が従う同時確率分布を P とします.
$$
\begin{aligned}
\quad E(Y|X \in A)\hspace{0.2em} := \hspace{0.2em}\sum_b b P(Y=b \mid X \in A)
\end{aligned}
$$
役に立つ知識
確率変数に関して知っておくと後々確率に関わる計算や定理をフォローするときに役立つ基本知識を解説無しにあげておきます.詳しくは確率の教科書を参照してください.
- 互いに独立の確率変数X,Yに対して
$$
\begin{aligned}
E(XY) = E(X)E(Y) \newline
V(X+Y) = V(X) + V(Y)
\end{aligned}
$$
- 確率変数Xに対して
$$
\begin{aligned}
V(X) = E(X^2) - E(X)^2
\end{aligned}
$$
- 確率変数列$${X_n,Y_n}$$に対して
$$
\begin{aligned}
X _ n \rightarrow _ {P} X,Y _ n \rightarrow _ {P} Y \text{ならば} \quad X _ n + Y _ n \rightarrow _ {P} X+Y \newline
X _ n \rightarrow _ {P} X,Y _ n \rightarrow _ {P} Y \text{ならば} \quad X _ n Y _ n \rightarrow _ {P} XY \end{aligned} \newline
X _ n \rightarrow _ {P} X,Y _ n \rightarrow _ {P} Y,Y \neq 0 \text{ならば} \quad X _ n / Y _ n \rightarrow _ {P} X / Y
$$
- (連続写像定理)確率変数列$${X_n}$$,連続関数$${g()}$$に対して,
$$
\begin{aligned}
X_n \rightarrow_{P} X \text{ならば} \quad g(X_n) \rightarrow_{P} g(X)
\end{aligned}
$$
- 条件付き期待値に関して
$$
\begin{aligned}
E(Y) \hspace{0.2em}= \hspace{0.2em} \sum_{a\in A}E(\hspace{0.2em}Y\hspace{0.2em}|\hspace{0.2em}X = a \hspace{0.2em} )\hspace{0.2em}P(X = a )
\end{aligned}
$$
1.2. 大数の法則と中心極限定理
標本 $${X = ( X_1,X_2,..,X_n ) }$$ の各要素は独立同分布の確率変数でありその平均 $${\bar{X}=(X_1+...+X_n)/n}$$ もまた確率変数です.標本平均 $${\bar{X}}$$ の期待値 $${E[\overline{X}]}$$を$${\mu}$$,標本分散の期待値 $${V[\bar{X}]}$$ を $${\sigma^2}$$ としましょう.
「大数の弱法則」(以後単に「大数の法則」とよぶ)は標本サイズ n が大きくなるにつれて標本平均 $${\bar{X}}$$ の値と期待値 $${\mu}$$ の差が極微になる確率が 1 に近づくという法則です.式で表すと,
$$
\begin{aligned}
\lim_{n \to \infty} P(∣\overline{X}-\mu∣ < \epsilon) = 1 \quad \epsilon\ は正の任意の数
\end{aligned}
$$
あるいは用語的な表現では,$${\bar{X}}$$は$${\mu}$$へ「確率収束」する,と言い以下のように表します.(別記事:「補足説明 確率・統計」)
$$
\begin{aligned}
\bar{X} \quad \rightarrow_P \quad \mu
\end{aligned}
$$
$${\bar{X}}$$ のように正規分布に確率収束する分布に従う確率変数は「漸近正規性」を有すると表現されます.
$${\bar{X}}$$ がしたがう分布は母集団の性質にかかわらず正規分布 $${N(\mu,\sigma^2/n)}$$ へ近づいていくという非常に重要な性質があります.これは数学的に証明することができ古くから「中心極限定理」として知られています.標準化されたスケールで表すと
$$
\begin{aligned}
Z = \frac{\overline{X}-\mu}{\sigma / \sqrt{n}}\quad とおいたとき
\end{aligned}
$$
$$
\begin{aligned}
\lim_{n \to \infty} P(Z < z) = \int_{-\infty}^{z}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} dx
\end{aligned}
$$
あるいは用語的な表現では,$${Z}$$ は N(0,1) へ「分布収束」する,と言い以下のように表します.
$$
\begin{aligned}
Z \quad \rightarrow_d \quad N(0,1)
\end{aligned}
$$
元の集団が正規分布に従っていてもいなくても,標本サイズ(標本の要素数のこと)n が大きくなるにつれ標本平均の分布が正規分布に近づいていていくという事実はきわめて有用です.
2. 「推定」というややこしい作業
2.1. 一致性,不偏性,有効性
「推定(estimation)」とは,統計量をもとに,正しいと考えられる統計モデルに基づいて母集団のパラメータ値を推測する試みです.標本から推定されたパラメータ値を「推定量(estimator)」とよびます.すでに定義がトートロジーになっていて居心地が悪いけれどがこのまま進めましょう.技術用語にしては硬さに欠けるこの言葉を有用にするために、推定という行為の良し悪しを評価する手段が必要となります.それが表題に現れる三つのキーワードです.
標本サイズが増大するにつれて推定量が真のパラメータに収束することを「統計的推定の一致性」といい,そのような推定量を「一致推定量(consitent estimator)」と呼称します.前述のように母集団と標本の性質から大数の法則が成立するので標本平均 $${\bar{X}}$$ は母平均の一致推定量です.一致性が無い、とはすなわち真の値に収束しない推定です.そのような量が役に立つとは思えません.したがって推定に用いる統計量を採用する前提として一致性は必須の要件といえるでしょう.
標本平均はその期待値が母平均と一致しています.このように母集団の真のパラメータ値と標本の推定量の期待値が一致する場合,これを「不偏推定量(unbiased estimator)」と呼びます.また,母集団の真のパラメータ値と推定量の差異を「バイアス」と呼びます.
一方,標本分散 $${V( X ) = \frac{1}{n}\sum_i^n(X-\overline{X})^2}$$ は一致推定量ですが,その期待値を計算してみると $${\frac{(n-1)}{n}\sigma^2}$$ となります.これは n→∞ で母分散に収束するものの,不偏推定量にはなっていません(参考:「補足説明 確率・統計」の 5.不偏性を持つ標本分散の定義).このように,不偏推定量にはなっていないが標本サイズが大きくなるにつれ推定量の期待値が母集団の真のパラメータに収束する場合その推定量は「漸近不偏性」を有するといいます.
まとめると,標本サイズを n,z を母集団のパラメータ,$${\hat{Z}}$$ をその推定量としたとき以下の定義が重要です.
一致推定量:$${ n \rightarrow \infty \text{のとき} \hat{Z} \rightarrow_P z }$$ (確率収束)が成り立つ
不偏推定量:$${ E[\hat{Z}] = z }$$ が成り立つ
漸近普遍性:$${ n \rightarrow \infty \text{のとき} E[\hat{Z}] \rightarrow z }$$ が成り立つ
不偏推定量は分析のために非常に有用な性質ですが,不偏推定量Aに対して期待値ゼロの統計量Yを足したA+Bも不偏推定量になります.つまり,ひとつの母数に対してユニークに不偏推定量が決まるわけではない点注意が必要です.ある母数に対して複数の不偏推定量があったときに,選択の指針になるのが「有効性(efficiency)」という概念です.有効性の尺度としては分散の大小を見ると良いといわれます.なおefficiencyは「効率性」と訳されることもあります.
不偏推定量Xの有効性が良い := 分散V[X]が小さい
上述した標本平均は母平均に対する最小の不偏推定量になっていることを証明できます.このような不偏推定量を「一様最小分散不偏推定量(Uniformly Minimum Variance Unbiased Estimator,UMVUE)」,あるいは簡単に「有効推定量」と呼びます.有効推定量が存在する場合の下限値も知られています.
クラメール-ラオ(Cramér-Rao)の不等式
母集団のパラメータ$${ \theta }$$に対する不偏推定量を$${ \hat{\theta} }$$とするとき,フィッシャー情報量J(Θ)との間に以下の関係が成り立ちます.
$$
V[\hat{\theta}] \quad \ge \quad \frac{1}{J(\theta)}
$$
ここでは下限が存在するという事実だけを記載しておきます.フィッシャー情報量など詳細は統計学の教科書を参照してください.
漸近不偏性を有する推定量の分散がクラメール-ラオの下限値に収束するとき「漸近有効性」を有するといいます.すなわち,
$$
n \rightarrow \infty \text{のとき} V[\hat{\theta}] \quad \rightarrow \quad \frac{1}{J(\theta)}
$$
漸近不偏性があれば大きな標本サイズでの推定の信頼性が高まると言えます.漸近有効性があれば大きな標本サイズでより小さな分散を得ることができます(つまり,より精度の高い推定ができる).推定量の漸近性はそのような有用性を主張しています.
ここまで書いただけでも推定の実務は作業対象のデータに応じて考慮する点が多々あって相当にややこしい印象を受けます.
よく使われる統計モデル
推定を実践し母集団の特徴を把握するためには数学的な手法を適用しやすい統計モデルを用意する必要があります.
よく使われる統計モデルには以下の種類があり,後述する点推定や区間推定,それぞれの目的に合った使われ方がされています.
- 線形回帰モデル:
線形回帰モデルでは,目的変数(予測対象)を説明変数(特徴量,観測データ)の線形結合としてモデル化するものです.
一般的な線形回帰モデルの統計モデル(=予測式)は次のように表現されます:
予測値 = $${ β_0 + β_1 * X_1 + β_2 * X_2 + ... + β_n * X_n + \epsilon }$$
ここで,$${β_0, β_1, β_2, ..}$$.は回帰係数で,$${X1, X2, ...}$$は説明変数,$${\epsilon}$$は誤差項.
- 時系列モデル:
時系列モデルでは,過去の観測値から未来の値を予測します.例えば,自己回帰モデル(ARモデル)では,過去のデータの線形結合として未来の値を予測します.
- 決定木モデル:
決定木モデルは,木構造を用いてデータを分割し,各葉ノードで予測値を生成します.
各葉ノードでの予測値は,そのノードに属する訓練データポイントの平均値または多数決などの方法で決定されます.
- ニューラルネットワークモデル:
ニューラルネットワークは多層のニューロンから成るモデルで,非線形関数を用いて予測値を生成します.
ニューラルネットワークの予測値は,入力データがネットワークを通過した結果として出力されます.
2.2. 点推定
「点推定(Point Estimation)」は,母集団のパラメータに対して単一の値(真の値)を推定する方法です.一般的な点推定方法には,最尤推定や最小二乗推定などがあります.以下主要な推定手法と具体的な使用例を見ていきましょう.
最小二乗法推定
最小二乗法推定(Ordinary Least Squares Estimation, OLSEあるいは単にLSE)は,観測データである実現値とモデルの予測値との誤差の二乗和を最小化するパラメータを母集団のパラメータの推定値とする手法です.幅広い予測モデルへ適用できるポピュラーな手法です.以下に線形回帰モデルを例とし,モデル式の切片と回帰係数を母集団のパラメータと考え最小二乗法により推定するプログラムをstatsmodelsのサンプルコードを紹介します.
#
# stat_estim_ols1.py
# テスト生成データを使い線形回帰モデルに対して最小二乗法推定を行う
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
import japanize_matplotlib
# サンプルデータ生成
np.random.seed(9876789)
X0 = np.random.normal(0, 0.9, size=100) # 正規分布に従った数値を観測データとして100個生成
y = 2 * X0 + 5 + np.random.randn(100) # 真の直線が傾き2,切片5になるよう係数を調整
# 線形回帰モデルクラス(OLS:Ordinary Least Squares)による最小二乗法推定
X = sm.add_constant(X0) # 説明変数として定数項を第0列に挿入
res = sm.OLS(y, X).fit() # 予測を実行
print(res.summary()) # パラメータ推定結果の表示
# 予測直線のパラメータを取得
intercept, slope = res.params
# プロット用のデータ
x_values = np.linspace(-3, 3, 100) # プロット用のX値(-2から2まで)
y_predicted = intercept + slope * x_values # 予測直線の式
Y = 2 * np.linspace(-3, 3, 100) + 5 # 真の直線の式
# プロット
plt.scatter(X[:, 1], y, label='観測データ') # サンプルデータ点の散布図
plt.plot(x_values, Y, color='blue', label='真の直線') # 真の直線
plt.plot(x_values, y_predicted, color='red', label='予測直線') # 予測直線
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title('線形回帰')
plt.show()
データをチャート化する

これを実行したときの処理結果レポート
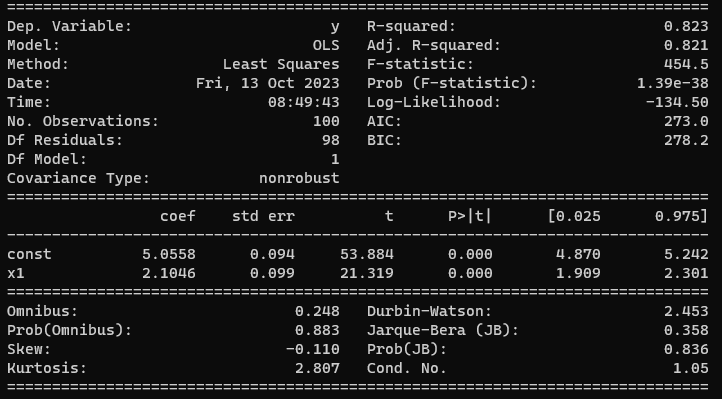
レポートの各項目の意味については別記事「データを準備する」のなかで説明をつけているので参照ください.
最小二乗法推定が特別であること
回帰モデルにおける最小二乗法推定が非常によい性質を持っていることが知られています.これについては別記事「回帰を活用する」のなかで補足しようと思います.
最尤推定法
母集団分布の形$${f(x;θ)}$$はわかっているけれどパラメータ $${\theta}$$ は不明であるようなケースにおいて,標本の統計量から $${ \theta }$$ を推定したいと考えたとします.f が正規分布ならば $${ \theta }$$ として平均 $${ \mu }$$ や分散 $${ \sigma^2 }$$ を想像してください.「最尤推定法(Maximum Likelihood Estimation, MLE)」では,試行により標本 $${ X=(X1,...,X_n) }$$ が観測されたとしたとき,その標本を得る確率 $${ L( \theta ) }$$ を定義しこれがが最大となる $${ \theta }$$ を母数の推定値と考えます.これを「最尤推定値」(=もっともらしい推定値)と呼称します.式で表すと
$$
\begin{aligned}
\theta_{MLE}=argmax_\theta L(\theta)
\end{aligned}
$$
ここで
$${ argmax_\theta A(\theta)}$$: Aを$${ \theta}$$の関数としたとき値が最大になる$${ \theta }$$のこと
母集団のパラメータが一つではなく複数の場合は多変量関数$${ L(\theta_1,...,\theta_m) }$$に対して同様に考えます.点推定は計算が比較的容易であり,1つの値を得ることができるため直感的です.ただし,推定の不確実性についての情報を提供しないので,不確実性の度合いを知りたい場合は後述の区間推定を使うことになります.
最尤推定量は,かなり一般的な仮定のもとで一致性,漸近的正規性 そして漸近的有効性を有することが証明されている,という記述をどこかのサイトで見ました.一方,最尤推定が有効である条件や制約についての記事もあります(最尤推定はいつなら大丈夫?(渡辺澄夫/東京工業大学)).詳細は推測統計学の教科書を参照してください.
最尤推定法の基本的なステップを示します:
尤度関数の設定: まず,観測データが得られる確率を示す $${ \theta }$$ の関数を定義し,これを「尤度関数(Likelihood Function)」と呼びます.この関数は,与えられたパラメータに対して,観測データが生成される確率を与えるものであるため母集団の分布関数の積として構成することができます.観測データを $${x=(x_1,...,x_n) }$$ とすると
$$
\begin{aligned}
L(\theta) = f(x_1;θ)f(x_2;θ)...f(x_n;θ) = \prod_{i=1}^{n}f(x_i;θ)
\end{aligned}
$$
例えば$${ \ f\ }$$が正規分布の場合には
$$
\begin{aligned}
L(\mu,\sigma^2)= \frac{1}{\sqrt{2\pi\sigma^2}}\exp(-\frac{\sum_{i=1}^n(x_i-\mu)^2}{2\sigma^2})
\end{aligned}
$$
対数尤度関数への変換: 尤度関数を対数変換して計算を簡単にし,数値的な見通しをよくします.このステップにより,母集団分布関数の積が対数和に変換されます.
$$
\begin{aligned}
\log L(\mu,\sigma^2) = -\frac{n}{2}\log( 2\pi ) -\frac{n}{2}\log( \sigma^2 ) -\frac{1}{2\sigma^2}\sum_{i=1}^n(x_i-\mu)^2
\end{aligned}
$$
argmaxの計算: 対数尤度関数を最大化するパラメータ $${ \theta }$$ の値を見つける.
このためには微分や勾配降下法などの最適化アルゴリズムを活用します.最尤推定では,尤度関数の対数尤度をパラメータ(上記例はμと$${ σ^2 }$$)について偏微分し,それをゼロと等置した方程式を解くことになります.
実際に $${log L }$$ に対して $${\mu}$$ に関する偏微分方程式を解いてみると $${\mu}$$ の最尤推定値 $${\hat{\mu}}$$ は観測データの平均に一致することがわかります.
$$
\begin{aligned}
\frac{\partial }{\partial \mu}\log (L(\mu,\sigma^2)) &= 0 \newline
\end{aligned}
$$
$${ \mu }$$に関する定数項は消えるので
$$
\begin{aligned}
-\frac{1}{\sigma^2}\sum_{i=1}^n(x_i-\mu) &= 0 \end{aligned}
$$
これを変形すると
$$
\begin{aligned}
\mu = \frac{1}{n}\sum_{i=1}^n(x_i)
\end{aligned}
$$
同じように$${ \sigma^2 }$$に関して計算すると$${ \sigma^2 }$$の最尤推定値$${ \hat{\sigma^2} }$$は観測データの分散に一致することがわかります.
$$
\begin{aligned}
\frac{\partial }{\partial \sigma^2}\log (L(\mu,\sigma^2)) &= 0 \newline
\end{aligned}
$$
$${ \log(p) }$$の微分が1/pであることを思い出すと
$$
\begin{aligned}
-\frac{n}{2}\frac{1}{\sigma^2}+\frac{1}{(\sigma^2)^2}\sum_{i=1}^n(x_i-\mu) &= 0
\end{aligned}
$$
これを変形すると
$$
\begin{aligned}
\sigma^2 = \frac{1}{n}\sum_{i=1}^n(x_i-\mu)^2
\end{aligned}
$$
推定されたパラメータの利用: 最尤推定法によって得られたパラメータの値を使用して,統計モデルの予測,推論,モデル適合度の評価などを行います.
科学技術計算用ライブラリscipyを使って実際に最尤推定を行ってみましょう.まずscipyをインストールします.
pip install scipy以下はscipyに含まれる正規分布確率密度関数を最適値としてを求める関数を使ったサンプルコードです.
# stat_estim_mle1.py
# 正規分布の平均を最尤推定する
#
import numpy as np
from scipy.stats import norm
from scipy.optimize import minimize
# サンプルデータ生成
np.random.seed(0)
data = np.random.normal(loc=5, scale=2, size=100)
# 尤度関数から対数尤度関数へ変換
def negative_log_likelihood(params, data):
mu = params[0] # 推定したい平均
# norm.pdf 確率密度関数
# loc 平均値 scale 標準偏差
likelihood = norm.pdf(data, loc=mu,scale=1)
log_likelihood = np.log(likelihood)
return -np.sum(log_likelihood)
# 最適化を用いて最尤推定を行う
initial_guess = [0.0] # 初期値
result = minimize(negative_log_likelihood, initial_guess, args=(data,))
mu_mle = result.x[0] # 最尤推定された平均
print(f"ランダム生成したサンプルデータの平均値: {5} 最尤推定された平均: {mu_mle:.2f}")
最尤推定量は良い性質を持つ?
まず尤度関数に関わる重要な統計量である「十分統計量」,そして十分統計量に関する重要な定理を示します.
- 十分統計量の定義
標本Xの統計量T(X)の実現値tのもとでXが実現値Xを得る条件付確率$${\hspace{0.2em} P(X=x\mid T(X)=t,\hspace{0.2em}\theta )\hspace{0.2em}}$$がθに依存しない時,そしてその時に限り,T(X) は母数$${ \theta }$$の「十分統計量(Sufficient Statistic)」であるという.
$$
十分統計量とは \Longleftrightarrow P(X=x\mid T(X)=t,\hspace{0.1em}\theta )=P(X=x\mid T(X)=t)
$$
十分統計量は観測データからパラメータ θ を推定するために必要な情報を保持しており,他の情報を追加で利用する必要がないことを示すものです.
- 因子分解定理
X の確率密度関数(離散的な場合には確率質量関数)をf(x ;θ) (これは尤度関数に等しい)とすると,ある関数 g と h が次の関係にある場合,かつその場合に限り,T はθ に対して十分である:
$$
{\displaystyle f(x,\theta )=h(x)\,g(T(x),\theta )}
$$
十分統計量 T(X) が与えられた場合,その条件付確率分布 P(X|T) はパラメータ θ に関する情報をすべて含むため,T(X) 自体から尤度関数をつくることでパラメータ θ を推定することができます.これはT(X) に関する条件付確率分布の特性を利用して推定する方法です.
$$
\begin{aligned}
\theta_{MLE}=argmax_\theta L_T(\theta;x) = argmax_\theta \hspace{0.2em} h(x)\,g(T(x),\theta )
\end{aligned}
$$
ベイズ推定法(Bayesian Estimation)
最尤推定法をはじめこれまでに述べた推定法は「頻度主義」という前提にたっています.頻度主義の立場では母集団の特徴を定めるパラメータはある定められた値をもち,観測データは確率的に変動すると考えます.推定値は観測データの統計量から導出される(最小二乗法推定),あるいは観測データがあらわれる確率を最大化するパラメータとして算出されます(最尤推定法).
これに対してベイズ推定法は,逆に母集団のパラメータは確率的にしか値を知ることができない不可知性(Uncertainty),不確実性をもったものと考えます.そして今パラメータに対してもっている不確実性をパラメータの「事前分布」として表現し,これを新しい観測値によってアップデートすることでパラメータの不確実性を減じていくというアプローチをとります.このアップデートされた分布をパラメータの「事後分布」と呼びます.ポイントは事前分布をどのように定めるのかとアップデートの方法です.
これまで分布と名のつく用語がいくつも出てきたましたが,事前分布とは母集団の分布関数とは異なる概念でありパラメータ自体の分布を決定する確率分布であることを再度強調しておきます.
事前分布の決定手法:
事前分布を適切に決定することは,ベイズ推定の結果に大きな影響を与えるため,慎重に手法を選択する必要があります.以下に事前分布を決定する一般的な手法を示します.
事前知識の利用:
事前分布をパラメータについての既存の知識や信念に基づいて設定する手法です.例えばドメインの専門知識や関連する研究から得られた情報を利用して,事前分布を決定します.
注)この決め方は,確率=頻度で慣らされた頭にはとっつきにくい感じがしますね.非情報事前分布(Non-Informative Prior):
特定の情報を反映しない分布を利用する手法.例えば,一様分布はわかりやすい例です.経験的ベイズ法(Empirical Bayes):
過去のデータからパラメータの事前分布を決める手法です.対象となる統計モデルに対する尤度関数を選択します.そして最尤推定法により観測データから事前分布のパラメータを推定します.事前分布は通常は特定の確率分布(例: ベータ分布,指数分布)を仮定し,その分布のパラメータを観測データから推定します.感度分析:
ベイズ推定では事前分布に対する感度分析を行うことが一般的です.事前分布のパラメータを変化させて結果の感受性を評価し,選択した事前分布が結果にどれだけ影響を与えるかを調べる手法です.
事前分布のアップデート:
ベイズの更新式は,ベイズの定理に基づいて尤度関数と事前分布から事後分布を計算する式であり,次のように表されます:
$$
事後分布 \ =\ 尤度関数 \ × \ 事前分布 \ / \ 正規化定数
$$
これを式で書くと以下のように表現できます:
$$
\begin{aligned}
P(θ∣x)= \frac{P(x∣θ)⋅P(θ)}{P(x)}
\end{aligned}
$$
ここで,各項の意味は以下の通り:
$${P(θ∣x)}$$ : 事後分布(Posterior),パラメータθ の条件付き確率分布で,新しい知識(やデータ)xにより更新された分布です.
$${P(x∣θ)}$$: 尤度関数(Likelihood),パラメータθ のもとでデータx が得られる確率を表します.これは実際の観測データに対するモデルの適合度を示します.
$${P(θ)}$$: 事前分布(Prior),パラメータθ についての不確実性を表す新しい知識(やデータ)により更新する前の確率分布です.
$${P(x)}$$: 正規化定数(Normalization Constant),事後分布を確率密度として正確に表現するための正規化定数です.通常は尤度関数と事前分布の積を全パラメータ空間にわたって積分することによって求められる(周辺化:marginalize)ことから「周辺尤度(marginal likelihood)」とも呼ばれます.
MAP推定法により事後分布の統計量をえる
MAP(Maximum A Posteriori)推定法は,計算量の問題で事後分布自体を求めることが難しい場合,かわりに事後分布内で最も確率密度が高い(最も尤もらしい)パラメータの値を求める手法です.
MAP推定値は単一の点推定であり,尤もらしいパラメータの値を提供します.これは事後分布の「ピーク」に対応するものです.MAP推定値は事後分布から得られる一つの統計値であり,パラメータの不確実性を考慮する点推定の手法といえます.
MAP推定値を以下の式で表します:
$$
\begin{aligned}
\theta_{MAP}=argmax_\theta P(\theta∣x)
\end{aligned}
$$
ここで,各記号の意味は次の通り:
$${ \theta_{MAP} }$$: MAP推定されたパラメータの値
$${ \theta }$$: 推定したいパラメータ
x: 観測データ
$${ P(θ∣x)}$$: パラメータ$${ \theta }$$の事後分布
右辺をベイズの更新式で置き換えたとき正規化定数の部分は$${ \theta }$$に依存していないので事後分布のargmaxは尤度関数×事前分布のargmaxに等しい.
$$
\begin{aligned}
argmax_\theta P(θ∣x)&= argmax_\theta \frac{P(x∣θ)⋅P(θ)}{P(x)}
\end{aligned}
$$
$$
\begin{aligned}
&= argmax_\theta P(x∣θ)⋅P(θ)
\end{aligned}
$$
例えば事前分布が $${\theta}$$ によらないものを考えれた場合には(例えば一様分布),これは最尤推定そのものです.この式の形から一般的には尤度関数に対する事前分布をうまく決めることがポイントになることがわかります.
うまい決め方のひとつとして「共役事前分布」をあげておきます.
これは尤度関数と事後分布が同じ関数の形になるように事前分布を決める方法です.
例えば母集団の分布関数が正規分布 $${N(\mu,\sigma^2)}$$ であった場合事前分布を以下 $${N(0,\sigma^2)}$$ として定義します.
$$
\begin{aligned}
P(\mu) = \frac{1}{\sqrt{2\pi\sigma_0^2}}\exp(-\frac{\mu^2}{2\sigma_0^2})
\end{aligned}
$$
これから方程式 $${ \frac{ d P(x∣\mu)⋅P(\mu) }{ d\mu } = 0 }$$ をとくと簡単な微分計算と式変形により $${ \mu }$$ のMAP推定値を得ことができます.
$$
\begin{aligned}
\mu_{MAP} \ =\ argmax_\theta P(\mu∣x) \ =\ \mu \ =\ \frac{\sigma_0^2}{n\sigma_0^2+\sigma^2}\sum_i^nx_i
\end{aligned}
$$
正規分布のように解析的な計算によりMAP推定値を得ることができる分布としては他にポアソン分布,ベルヌーイ分布,指数分布などがあります.
事後分布の計算1 解析的に求められるパターン
(省略)
その他の事後分布の計算方法 マルコフ連鎖モンテカルロ法(MCMC)
機械学習や予測でよく使われるこの手法については別記事で補足します.
2.3. 区間推定
不確実性の認識と信頼度:
母集団のパラメータは確定した真の値をもつという前提は点推定と共通しつつ,区間推定(Interval Estimation)では,我々が行う統計的推定行為には不確かさがあるという前提にたちます.その不確かさを測る指標として「信頼度(信頼水準)」を事前に設定します.95%や99%などの値がよく使われるようです.推定対象パラメータを $${ Param }$$,信頼度を95%に設定したとしましょう.このとき $${ |Param|<v }$$ で決まる幅2vの区間に95%の確率で真のパラメータを発見できる,と判定した場合この区間のことを「信頼区間」と呼びます.信頼区間を決定することを一般に区間推定と呼びます.
信頼区間の計算:
以下に主要な区間推定の方法を示します.
Zスコアによる推定:
Zスコアは,正規分布に従う観測データ$${X}$$が母集団の平均からどれだけ標準偏差の数値分離れているかを理解しやすいよう変換したものです.
$$
\begin{aligned}
Z = \frac{X-\mu}{\sigma}
\end{aligned}
$$
ここでX は観測データ,μ は母集団の平均,σ は母集団の標準偏差です.
標本平均 $${ \bar{X} }$$ もまた正規分布に従い,そのZスコアは以下の式となります.
$$
\begin{aligned}
Z = \frac{\overline{X}-\mu}{\sigma/\sqrt{n}}
\end{aligned}
$$
この式の分母に現れる量を「標準誤差(Standard Error, SE)」といいます.
$$
\begin{aligned}
SE = \frac{\sigma}{\sqrt{n}}
\end{aligned}
$$
観測データ $${X}$$ が正規分布に従わない場合であっても中心極限定理が示すように標本平均の Z スコアは n が十分大きければ近似的に正規分布に従います.そこで信頼度を α,これを実現する区間幅を $${ z_{conf} }$$ とすると,信頼区間の定義から
$$
P(-z_{conf} \ \le\ \frac{\overline{X}-\mu}{SE} \ \le\ +z_{conf}) \ =\ \alpha
$$
P の括弧内の論理式は以下と同値
$$
P(\bar{X}-z_{conf}\cdot SE \ \le\ \mu \ \le\ \bar{X}+z_{conf}\cdot SE) \ =\ \alpha
$$
つまり信頼区間の推定値は標本平均からずれの下限,上限として以下のように求められます.
下限 = $${ \bar{X}-z_{conf} \cdot SE }$$
上限 = $${ \bar{X}+z_{conf} \cdot SE }$$
具体的な数値は公開されているZ分布表(例:産総研のZ分布表)を利用することで容易に信頼区間の推定値を得ることができます.

上図で左側の赤丸はZスコアの小数点1位までの数字が「1.9」であることを示しています.上方の赤丸は小数点2位の数字が「6」であることを示しています.1.9の横軸と6の縦軸の交点の数字「0.024998」が信頼度を表します.すなわちZ<=1.96となる確率が約2.5%であることを示すものです.信頼度の設定を正あるいは負どちらかに限定することを片側推定といい,正負両方設定した場合を両側推定と呼ぶ習慣があるので信頼度5%での両側推定の信頼区間は|Z|<=1.96ということになります.
言葉の使い方
信頼度95%の信頼区間は |Z| <= 1.96 である.
|Z| <= 2 であるとき 「Zは2シグマ以下である」という.信頼度95.45%の信頼区間を示す.
Tスコアによる推定:
Z スコアによる推定は母分散が既知であることを前提としています.また n が小さくなるほど推定の誤差は増えていきます.T スコアによる推定はこのような Z スコアが適用できないケースにも対応できるため実務ではよく使われます.
T スコアの背後にある考え方は,母集団の平均に関する統計的な推定を行う際に,標本サイズの大きさが小さい場合に生じる不確かさ(標本誤差)を補正することです.
不明な母分散 $${\sigma^2}$$ の代わりとなる量が必要となります.答えは「標本不偏分散」$${s^2}$$ と呼ばれる確率変数を定義し置き換えることです.標本不偏分散の平方根は「標本標準偏差」と呼ばれることがあります.少し紛らわしい言葉の使い方のように感じますね.
$$
\begin{aligned}
s := \sqrt{ \frac{1}{n-1}\sum_i^n(x_i-\overline{X})^2 }
\end{aligned}
$$
日次の株価 $${P_t}$$ からなる時系列から算出した標本標準偏差は株価分析の世界ではボリンジャーバンドとしてよく知られています.また,対数株価変動率 $${ X_t = \ln ( \frac{ P_t }{P_ {t-1} } ) }$$ に対する標本標準偏差はヒストリカルボラタリティと呼ばれ,株価の値動きの大きさを示す指標として使われています.
$$
\begin{aligned}
H_v := \sqrt { \frac{1}{n-1}\sum _ { i = t - n } ^ t ( X _ i - \overline{X})^2 }
\end{aligned}
$$
標準誤差の式が $${\sigma/\sqrt{n}}$$ であったのでこれを置き換えるのであれば式 $${\sum_i^n(x_i-\overline{X})^2/n}$$(標本分散と呼ばれる確率変数)を使ったほうが自然のようにも思えますが,これはうまくいきません.実際にこの確率変数の期待値を計算してみると得られるのは,$${(n-1)\sigma^2/n}$$ という母数 $${\sigma^2}$$ よりも小さな数字であり不偏性が損なわれているからです.そこで上記のように定義しておけば,$${E[s^2]}$$は$${ \sigma^2}$$に一致する不偏推定量となっていることが少し計算するとわかります.
標本標準偏差($${s/\sqrt{n}}$$)によりZスコア式を修正した結果が以下の T スコアです.
$$
\begin{aligned}
T = \frac{\overline{X}-\mu}{s/\sqrt{n}}
\end{aligned}
$$
ここで $${ \bar{X}}$$ は標本の平均,μ は母集団の平均,s は標本標準偏差(=標本不偏分散の平方根),n は標本サイズ.
Tスコアが従うT分布の信頼区間の推定値は標本平均からずれの下限,上限として以下のように求められます.信頼度をα,これを実現する区間幅を $${t_{conf}}$$ として,
下限 = $${\bar{X}-t_{conf}\cdot s/\sqrt{n}}$$
上限 = $${\bar{X}+t_{conf}\cdot s/\sqrt{n}}$$

上図は比較のため T 分布の自由度1,2のグラフと標準正規分布のグラフをexcelを使って書いてみたものです.T分布はT.DIST関数,正規分布はNORM.DIST関数で計算したものを散布図で容易にグラフ化にできます.自由度は標本サイズ(=標本あたりの観測データ数)から1を引いた数として定義されるため,自由度1のグラフは標本サイズ=2のときに適用されます.
信頼度 α を決める(例えば95%)と,T分布表(参考:産総研のT分布表)から信頼区間を確認することができます.T分布の密度関数の式形は少し複雑なので割愛します.考案者(ゴセット)がどのような過程でT分布を発見したのか筆者は調べていませんが本稿の目的には T 分布の公式を知らなくてもよさそうなのでこれ以上立ち入らないことにします.
参考
3. 統計的に有意とはどういうことですか?
統計の世界ではある命題の真偽を判定するために計画された実験や調査があったとして,その命題を肯定する結果が偶然に出現したとは考えにくい場合,命題が真であると考え「統計的に有意な」結果が得られたと言明します.ここに出てきた「偶然に出現したとは考えにくい」を判定する基準を数値化し「有意水準(significance_level)」あるいは「危険率」と呼称します.これを指すのにしばしば記号 α が用いられます.有意水準は実験や調査の内容に応じて決められるべき数値ですが,以下のようなとらえ方がよく行われているようです.
5%以下の出現率 → 小さい
1%以下の出現率 → 非常に小さい
0.1%以下の出現率 → 極端に小さい
「100%正しい」、も「100%間違っている」も無い世界で真偽を定義するアイデアとして、便宜的な感じがしつつも便利には違いないと思います.
帰無仮説
目的とする母集団の特徴を知るということを統計の手法では真偽を判定できる命題の形で表現します.例えば仮説した統計モデルの正しさを検証する等,真偽を証明したい命題に対して,その命題が偽であると仮定することを「帰無仮説(Null Hypothesis)」を設定すると表現します.そして試行から得られたデータをもとに帰無仮説を肯定する結果が出現する確率を計算します.それがあらかじめ定めた有意水準(例えば5%)以下であれば,帰無仮説を棄却(否定)します.つまり帰無仮説の反対を主張するもともとの命題(「対立仮説」と呼ばれる)が真であると判定します.
少し言い換えると帰無仮説は対象とする命題が偶然に成立することはさほど珍しいことではないと主張します.しかしその前提で計算してみると極めて稀にしか成立しない命題であることが判明したとします.するともっともらしい結論とは,帰無仮説は誤りであり対象とする命題が成り立つことは偶然ではなく必然だろうとする判断です.
まわりくどい感じもするのですが,「仮説」が正しくないことを証明するためには反例がひとつでも見つかればOKなので,背理法に従ったこの考え方は合理的であるといえます.ただし帰無仮説が棄却されなかった場合何がわかったのかというと,「対立仮説が正しいとはいえない」であって「対立仮説は誤っている」ではない,ということに注意が必要です.
このようにして得られた試行結果をもとに帰無仮説が真であることを証明する作業を「検定(Test)」と呼称します.具体的な手順として帰無仮説を証明するための定量的指標をまず定めます.これを「検定統計量(test statistic)」とよびます.帰無仮説が成立すると仮定したうえで標本に対する検定統計量を算出し,その出現確率が有意水準を下回るのであれば,帰無仮説を棄却する.そうでなければ対立仮説を受容します.
3.1. 帰無仮説を使って超能力の存在を証明したい!
参考2の「推計学のすすめ」という本に記載されていた題材がおもしろっかたのでこれを補強して帰無仮説を説明してみましょう.
唐突だけれどサイコロ投げという行為を通じて「超能力は存在する」という命題をたてその真偽を判定したいと私は考えました.これを証明するための実験としてサイコロを1000回振って念じて偶数を出現させる試行を行おうと思います.
母集団は無限に続くサイコロ投げ,標本は一定回数投げて出た目の集合とする.帰無仮説(H0)は「超能力は存在しない」,対立仮説(H1)は「超能力は存在する」.有意水準を5%と設定します.
検定統計量は,念じて偶数を出現させた回数(例えば,偶数の出現回数)を用います.帰無仮説の下では超能力が存在しないと仮定されているため,偶数が出現する確率は通常のサイコロの確率(1/2)と同じであると仮定します.
検定のステップ:
サイコロを1000回振る試行を実行し,偶数が出現する回数を検定統計量と決め記録する.
試行で得られた検定統計量の値を与える確率を算出し有意水準と比較する.
計算した確率が有意水準以下であれば帰無仮説を棄却し「超能力は存在する」と判定する.そうでない場合ば「超能力が存在するとはいえない」と判定する
試行の結果:
偶数の出現数 → 542
奇数の出現数 → 458
帰無仮説の判定:
均等に目が出るサイコロを振ったときに指定回数k以上の偶数が出る確率は2項分布を使って求めることができます.
$$
\begin{aligned}
P(X \ge k) = 1- \sum_{i=0}^{k-1}
\left( \begin{array}{c}
n \newline
i \newline
\end{array} \right)
\cdot p^i \cdot (1-p)^{n-i}
\end{aligned}
$$
$${P(X \ge k)}$$ は,k回以上成功(偶数が出る回数)する確率.
n は1回の試行に含まれる標本数(この試行では1000).
k は成功回数(=542).
p は1回の試行で成功する確率(偶数が出る確率)で,1/2.
$${ \left( \begin{array}{c} n \\ k \end{array} \right) }$$ はn回中k回成功する組み合わせの数 $${_nC_k= \frac{n!}{k!(n-k)!} }$$であり二項係数と呼びます.
ExcelのBINOM.DIST関数あるいはscipyのbinom.cdf関数など,二項分布の確率分布関数をサポートするツールで計算すると約0.358%を得ます.これは有意水準5%をかなり下回るので偶数の目が出た回数542回は偶然に出現するとは考えられず,結論として帰無仮説は棄却され,「超能力は存在する」と推定ます.有意水準との比較に使われた $${P(X \ge k)}$$ を p 値と呼びます.
蛇足ですが有意水準に対応する偶数出現数を計算すると526という数字が出ます.この程度のばらつきは何回か試行するとなんとなく容易に出現しそうな気もするのですが実際にはありえないほどレアということです.
手法の一般化,Z検定:
上述したExcelのBINOM.DIST関数が二項分布をどういうアルゴリズムで出力しているのか筆者は知りませんが,一般に検定統計量が現実的な時間では計算できない場合もあるでしょう.そのような場合であっても中心極限定理が成り立つ条件さえ満たせていれば検定統計量が従う分布として正規分布を使うことができます.二項分布の場合では,分布の期待値E,分散Vはそれぞれnp,np(1-p) であること,さらに二項分布は標本サイズnが大きい場合期待値np,分散np(1-p)の正規分布の確率密度関数へ近似することが古くからド・モアブル=ラプラスの極限定理として知られています.
$$
\begin{aligned}
X \quad \sim \quad \frac{1}{\sqrt{2\pi np(1-p)}}\exp(-\frac{(k-np)^2}{2np(1-p)})
\end{aligned}
$$
したがって二項分布に従う統計量をXとしたとき標本サイズが大きければ
$$
\begin{aligned}
Z \quad = \quad \frac{X-np}{\sqrt{np(1-p)}}
\end{aligned}
$$
は近似的に標準正規分布に従います.この式と標準正規分布表をつかって前述のP(X>=k)を算出してみると0.40%というけっこう近い値が出てきます.離散分布の2項分布を連続分布の正規分布で近似する際に現る差異を補正するために定数0.5を上記Zの定義式分子に加えることを連続補正といいます.連続補正によりZの定義式分子をX+0.5-npで置き換えると近似はもっと良くなり約0.362%という値がでてきます.
平均と分散があらかじめわかっている正規分布に従うZスコアを統計量として使用する検定手法はZ検定と呼ばれます.この事例では母集団(=サイコロを振って出た目の列)の平均と分散が既知であったためうまい具合にZ検定を適用することができました.$${\bar{X}}$$ を標本平均,$${\mu}$$ を母集団の平均,n を標本サイズ,$${\sigma}$$ を母集団の標準偏差(分散の平方根のこと)としたときのZスコアを再掲します
$$
\begin{aligned}
Z \quad = \quad \frac{\overline{X}-\mu}{\sigma / \sqrt{n}}
\end{aligned}
$$
Z検定の適用シーン
「Z検定(Z-test)」は,特に母集団の平均や比率に関する仮説を検定するために広く使用される手法です.以下に,Z検定がよく使われる適用シーンをいくつか示しておきます.
標本平均の母集団平均との比較(1標本の検定):
単一の標本から得られた平均値$${ \mu }$$が,ある既知の母集団平均$${ \mu_0 }$$と統計的に異なるかどうかを判定するためにZ検定を利用できます.例えば,ある製品の平均寿命が既知の平均寿命と等しいかどうかを検証する場合です.$${ \mu - \mu_0=0 }$$ を帰無仮説とし,これが棄却される結果を得たならば標本の平均と母集団の平均には有意差があると判定できます.母集団の平均の比較(2標本の検定):
Z検定は,2つの独立した標本それぞれの平均値 $${ \mu_0,\mu_1 }$$ が統計的に異なるかどうかを判定するためにも利用できます.例えば,新しい薬の治療効果を評価するために,治療群と対照群の平均体温を比較する場合です.$${ \mu_0-\mu_1=0 }$$ を帰無仮説とし,これが棄却される結果を得たならば二つの母集団の平均には有意差があると判定できます.母集団の比率の比較:
カテゴリカルデータの比率を比較する場合,Z検定は非常に有用です.例えば,2つの異なる広告キャンペーンのクリック率を比較して,どちらが優れているかを判断する場合などに適用できるでしょう.大規模なサンプルサイズの場合:
母集団が正規分布にしたがっていないとしてもサンプルサイズが十分に大きい場合,中心極限定理に基づいてZ検定を適用することができます.十分に大きいの目安はn=30とされているようです.
母集団の分散が既知でないとき,T検定:
残念ながら現実の応用場面では母集団の平均,分散が既知であることはまれです.そのため母集団の分布は正規分布であるが平均,分散は不明であるという前提での検定手法が一般によく用いられる「T 検定」です.T 検定では前出のT スコアを検定統計量として使用する手法です.
$$
\begin{aligned}
T \quad = \quad \frac{\overline{X}-\mu}{S / \sqrt{n}}
\end{aligned}
$$
ここで $${S^2}$$ は標本不偏分散.
T検定の適用シーンはZ検定と同様です.
1標本検定の場合は母集団の平均 $${\mu_0}$$ は既知として,$${\mu - \mu_0=0}$$ を帰無仮説として設定します.これが棄却された場合標本の平均と母集団の平均には有意差があると判定できます.
2標本検定の場合は,ふたつの母集団の平均の差を検定します.母集団の平均の値自体は問わず,分散は不明という前提となります.Z検定のときと同じく標本平均の差 $${\mu_0 - \mu_1=0}$$ を帰無仮説とし,これが棄却される結果を得たならば母集団の平均には有意差があると判定できます.
棄却域とP値:
「棄却域(Rejection Region)」とは,帰無仮説が成立すると仮定した場合に,検定統計量の出現確率が有意水準と同じか下回る領域を意味します(下図の黄色でハッチした部分).棄却域に入らない領域を信頼区間と呼びます.棄却域と信頼区間の境界の検定統計量の値を「臨界値(critical value)」とよびます.
「P 値(P-value)」は,帰無仮説が成立すると仮定した場合,標本から計算した検定統計量の出現確率以下になる領域に検定統計量が入る確率を示す数値です.従ってP 値が有意水準以下となる場合には帰無仮説は棄却されます.一方P値が有意水準以上の場合,帰無仮説は棄却されません.
棄却域として分布の右側あるいは左側の一方だけを使う検定を片側検定といい,両方使う場合を両側検定といいます.両側検定では有意水準を5%とした場合右側,左側それぞれ2.5%の有意水準として計算します.

3.2. 仮説検定のなかで現れる誤りのパターン
仮説検定では命題の真偽が便宜的であるだけに,帰無仮説 $${H_0}$$ を判定した結果偽であるとし棄却した場合であっても実際のところは真であったという場合が当然起こりえます.この判定と真実の関係は以下の混同行列と呼ばれる四象限の表で表すことができます.この行列表現は機械学習におけるクラス分類モデル(分類アルゴリズム)の予測結果と実際のクラス(正解ラベル)との一致や不一致を表現する際にも頻出する重要な概念です.
検定の適用シーンによってはよく使われる用語がありますので表に付記しました.例えば感染症の陽性を検出する機器による検査を想定し「($${H_0}$$)検査機器は無効であり,正確な結果を提供しない」を帰無仮説とし,「($${H_1}$$)検査機器は有効である」を対立仮説とする検定を想定すると理解しやすいと思います.

表中4つの主要な要素が含まれます:
帰無仮説を棄却する:
真陽性(True Positive, TP):対立仮説が正しいと検定し,真実も対立仮説が正しかった.
偽陽性(False Positive, FP):対立仮説が正しいと検定したが,真実は対立仮説が誤っていた.
帰無仮説を棄却しない:
真陰性(True Negative, TN):帰無仮説が正しいと検定し,真実も帰無仮説が正しかった.
偽陰性(False Negative, FN):帰無仮説が正しいと検定したが,真実は帰無仮説が誤っていた.
試行により得られた観測データの構成比率は検定の性能を評価する指標となります.以下は主要な指標です.
正解率(Accuracy):真の陽性,真の陰性が正しく判定された観測データの割合
$$
\begin{aligned}
Accuracy = \frac{TP + TN} {TP + TN + FP + FN}
\end{aligned}
$$
適合率(精度)(Precision):陽性と判定された観測データのうち,真は陽性である割合
$$
\begin{aligned}
Precision = \frac{TP} {TP + FP}
\end{aligned}
$$
再現率(感度)(Recall):真は陽性の観測データのなかで,正しく陽性と判定された割合
$$
\begin{aligned}
Recall = \frac{TP} {TP + FN}
\end{aligned}
$$
F1スコア(F1 Score):適合率と再現率の調和平均で,対立仮説のバランスを示す指標.
$$
\begin{aligned}
F1-score = 2 * (適合率 * 再現率) / (適合率 + 再現率)
\end{aligned}
$$
第一種過誤と第二種過誤は表中トレードオフの位置になっているため同時に減らすことはできません.統計の標準的な考え方では検定の誤りを減らすためにはまず適合率(精度)を向上させ第一種の過誤となる確率 α(有意水準)を一定以下にすることを優先します.そのたうえで再現率(感度)を向上させることで第二種の過誤となる確率βを減らす検討をすることが一般的のようです.1-β は検出力とも呼ばれます.ただし重要な指標は検定の目的によって決めるべきものであるため必ずしもこの指針が絶対というわけではありません.実際,新型インフルエンザ流行が激しかった頃の報道を思い出すと真の陽性を見逃さないために検査機器の感度の高さ(第二種過誤を減らすこと)が求められていたように思います.
次に株価予測モデルの有効性を検定する作業を考えてみましょう.有効な株価モデルとは「上昇すると予測した株価が実際に上昇する」,上昇的中率が高いモデルであると考えることにします.「($${H_0}$$)予測モデルは無効であり,正確な結果を提供しない」を帰無仮説とし,「($${H_1}$$)予測モデルは有効である」を対立仮説とする検定を想定ましょう.上昇予測数に対する上昇的中数の割合の分布を測定し検証した結果帰無仮説が棄却されたなら予測モデルは有効だ!と判定する,という流れです.下表でいえば観測データのなかで (TP + FP) に占める TP の割合が非常に高い場合が予測モデルが有効である考える根拠になると言えます.筆者はロスカット発生を恐れる性分なのでこの予測モデルで重視したいのは,実際には値下がりする株を値上がりすると予測する誤りが少ないことです.そうすると第一種の過誤を減らす指標として偽陽性率 (False Positive Rate, FPR) FP / ( FP + TN ) の低減を指標として予測モデルを改良していくことが目的に合っていると結論できます.

参考資料 確率・統計 補足説明集
この章の参考文献とリンク
前の章 データを準備する
この記事が気に入ったらサポートをしてみませんか?
