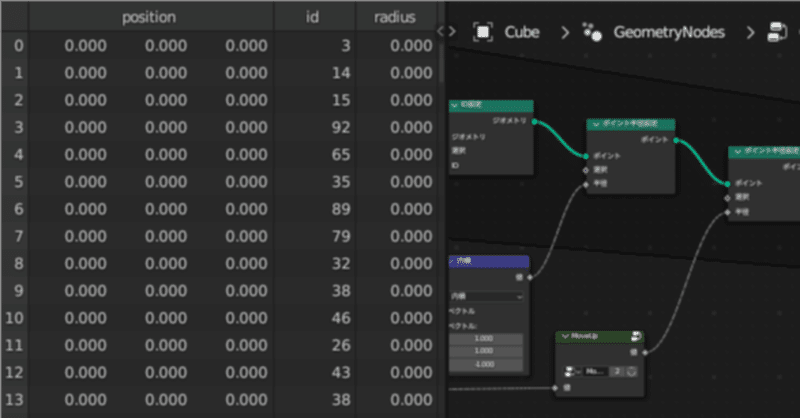
BlenderのGeometryNodesで円周率10000桁を計算する
GeometryNodes、大抵何でもできるので、円周率ぐらいサクッと計算できるだろってことで、やってみました。
BlenderのGeometryNodesで円周率10000桁計算しました#Blender #b3d #geometrynodes pic.twitter.com/CQ8xCYaQcx
— Melville (@MelvilleTw) April 8, 2023
準備
今回はBlenderの2023年4月現在アルファ版となっている機能を使用します。
Geometry Nodes Simulation という機能で、専用のブランチで開発が進められていますが、定期的にビルドされており、以下のページからダウンロード可能です。
ダウンロードして展開し、フォルダ中にあるアプリを立ち上げるとアルファ版Blenderを起動することができます。
実装
逆正接関数 arctan
円周率を求める方法は様々考案されていますが、今回は逆正接関数 $${ \arctan x}$$ を用いた方法を採用します。
逆正接関数 $${ \arctan x}$$ は正接関数 $${ \tan x}$$ の逆関数であり、その定義より次の式が成り立つことがわかります。
$$
\arctan 1 = \frac{ \pi }{ 4 }
$$
すなわち、単に $${ \arctan 1}$$を4倍するだけでも円周率の計算が可能です。
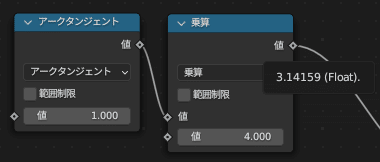
GeometryNodesの計算は float (32bit浮動小数点数) で行われるため、この時点ではだいたい7桁の精度で円周率が求まります。
しかし、今回は10000桁計算させたいので、色々と工夫が必要になります。
テイラー展開
上では「アークタンジェント」という便利なノードを使ったのですが、これに頼れるのは最初の7~8桁だけです。
10000桁計算させるためには自前で $${ \arctan}$$ の値を求めなければなりません。
$${ \arctan x}$$ は次のように"展開"できることが知られています。
$$
\arctan x = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \frac{x^9}{9} + …
$$
$${ x = 1}$$ を代入すると、
$$
\arctan 1 = 1- \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} + …
$$
のように奇数の逆数を交互に引いたり足したりすることで $${ \arctan 1}$$ が求まることを意味します。(これはライプニッツの公式と呼ばれています)
円周率はこの4倍なので、分子を全部4にして足せば円周率が求まることになります。
$$
\pi = 4\arctan 1 = 4- \frac{4}{3} + \frac{4}{5} - \frac{4}{7} + \frac{4}{9} + …
$$
しかし、これは収束が遅いです。
実際にやってみると、4/17まで足しても3.25237…となので、数桁求めるだけでも相当項を増やす必要があることが推察されます。

Geometry Nodes Simulation
ここで Geometry Nodes Simulation が大活躍します。
このノードを使うと、ひとつ前のフレームの計算結果を現在のフレームに持ち込むことが可能になります。

フレーム数の回数実行されるイメージ
GeometryNodesは繰り返し処理が苦手なのですが、つまるところこのノードを使うと簡単に繰り返し処理が実装可能です。
具体的には次のようにノードを構築し、Blenderの再生ボタンを押すことで終了フレームに達するまでの間、奇数の逆数を引いたり足したりし続けることができます。

実際にやってみると、次のようになります。

(ちなみにこれは重要な小ネタですが、
再生中にスプレッドシートのスクロールバーの少し左にマウスカーソルをあてるとリアルタイムに値が更新されるのが確認できて便利です。)
500個項を足してようやく3桁求まるというのはだいぶ遅いのです。
もっと効率的な公式があります。
arctan を分解する(マチンの公式)
$${\arctan}$$ を"分解"すると一般的に高速化が期待できます。
$${\tan}$$ の加法定理より、$${ab = n^2+1}$$を満たす整数$${a, b}$$を用いて次のような分解が可能です。
$$
\arctan \frac1n = \arctan \frac1{n+a} + \arctan \frac1{n+b}
$$
例えば$${n = 1}$$のとき、$${a = 1, b=2}$$を用いれば、
$$
\arctan 1 = \arctan \frac1{2} + \arctan \frac1{3}
$$
ですし、$${n = 2}$$のとき、$${a = 1, b=5}$$を用いれば、
$$
\arctan \frac{1}{2} = \arctan \frac1{3} + \arctan \frac1{7}
$$
のように分解でき、つまり
$$
\arctan 1 = \arctan \frac1{3} + \arctan \frac1{7}
$$
も成り立ちます。
このようにして $${\arctan 1}$$ の分解を無数に考えることができます。
この方法を用いてパズルのように様々な分解を考えることができ、この中でも特に有名なものは次のような分解です。
$$
\arctan 1 = 4 \arctan \frac1{5} - \arctan \frac1{239}
$$
これはマチンの公式と呼ばれています。
$${\arctan x}$$のテイラー展開が
$$
\arctan x = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \frac{x^9}{9} + …
$$
であることを思い出し、$${x}$$に$${\frac{1}{5}}$$と$${\frac{1}{239}}$$を代入すると、
$$
\arctan \frac{1}{5} = \frac{1}{5} - \frac{1}{3 \cdot 5^3 } + \frac{1}{5 \cdot 5^5 } - \frac{1}{7 \cdot 5^7 } + \frac{1}{9 \cdot 5^9 } + …
$$
$$
\arctan \frac{1}{239} = \frac{1}{239} - \frac{1}{3 \cdot 239^3 } + \frac{1}{5 \cdot 239^5 } - \frac{1}{7 \cdot 239^7 } + \frac{1}{9 \cdot 239^9 } + …
$$
がわかります。
試しに2項ずつ計算すると、この時点で「3.14」まで求まっています。

先程と同様に Simulation を組むと次のようになります。


これで公式が有効そうであることは確認できたのですが、結局floatで計算しているので精度の問題はまだ解決していません。
多倍長固定小数点数演算
10000桁求めるにあたって、ポイント半径1つに結果を格納するのは、情報量的に足りません。
そこで、ポイントを複数(例えば2000個)用意して、それぞれのポイントに5桁ずつ値を格納していい感じに計算すれば良さそうです。
しかしここで、GeometryNodesは整数の演算ができないという非常に重大な問題があります。
符号なし32bit整数であれば、0 から 4,294,967,295 までの値が扱えるのに対し、32bit浮動小数点数は指数部にもbitが割かれているため実質的にまともに整数が扱える範囲は 0 から 16,77,7,215 までです。
この範囲を超えないように意識しながら設計する必要があります。
結論から言うとポイント1つに対して2桁を割り当てて計算し、ポイントを5000個と追加で少し(例えば5005個)用意するというのが今回10000桁求める上で最適です。
例えばこの方法を使ってポイント5個を使って「3」を表すと次のようになります。

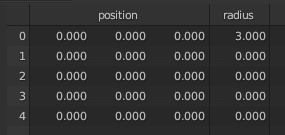
2桁ずつ読むことにすると、これは「3. 00 00 00 00」と読める。
値の表示方法を確立したので、いよいよ本格的な実装に入っていきます。
割り算の実装
今回の試みの最大の難関がここです。
ここでは筆算でやる操作を愚直に実装します。
(そんなに特殊なことはしていないので詳しい説明は割愛します)
まずは簡単な例としてポイント5個を作成して3を7で割る例を示します。


結果は次のようになります。

結果は 0.42857142 となり、うまく計算できていることが確認できます。
この実装ではDivideをポイントの個数分並べる必要があります。
つまり1000個のポイントを作るとしたら何も工夫しない場合1000個ノードを接続する必要があり、これは現実的ではありません。
割り算だけであればSimulationノードを使う手段も考えられますが、Simulation内で割り算を使用したいため、Simulationを使わずに実装する必要があります。
これはグループをいくつか繋いだものをさらにグループ化することを多重に行うことで、必要最小限の作業で実現することができます。
例えば次のような接続で256個分接続したことになります。

これで割り算が実装できたので、Simulation Input/Outputで挟み込むことにより、毎フレーム7で割り続ける処理が実現できます。


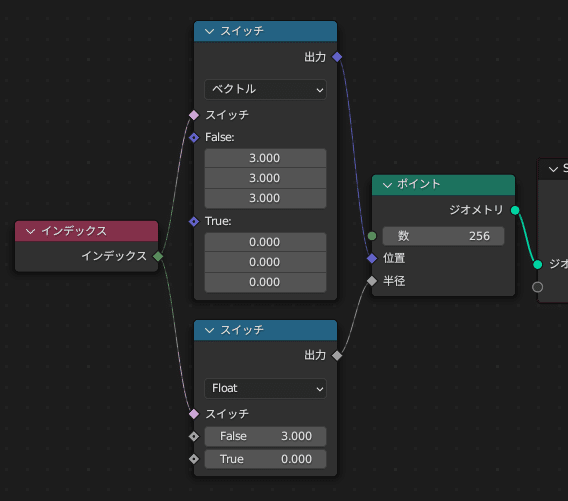
複数の割り算を同時に行う
ポイントは半径だけでなく位置も属性として利用可能なので、位置とポイント半径を同時に処理すれば4つの割り算を一気に行うことができ、後々これが効果的にはたらきます。


マチンの公式の実装
割り算も実装できたので、マチンの公式を実装します。
公式を改めて再掲します。
$$
\pi=4\arctan 1 = 16 \arctan \frac1{5} - 4 \arctan \frac1{239}
$$
またここで、
$$
\arctan \frac{1}{5} = \frac{1}{5} - \frac{1}{3 \cdot 5^3 } + \frac{1}{5 \cdot 5^5 } - \frac{1}{7 \cdot 5^7 } + \frac{1}{9 \cdot 5^9 } + …
$$
$$
\arctan \frac{1}{239} = \frac{1}{239} - \frac{1}{3 \cdot 239^3 } + \frac{1}{5 \cdot 239^5 } - \frac{1}{7 \cdot 239^7 } + \frac{1}{9 \cdot 239^9 } + …
$$
です。これを行うのは、次の処理を適切な順序で行えば良いです。
位置 X : 初期値を20(=4*5)とし、毎フレーム25(=5²)で割り続ける
位置 Y : 初期値を956(=4*239)とし、毎フレーム57121(=239²)で割り続ける
位置 Z : 未使用
半径 : 現在の値を(フレーム数*2-3)で割ったものをIDに足したあと、偶数フレームでは-4X+Y、奇数フレームでは4X-Yの値に置き換えておく
ID : 適切に繰り上がり/繰り下がり処理を行う
計算用に位置と半径を使用したかったので結果はIDで表すようにしました。
これを実装したものがこちらです。

また、Divideノードの割る数も、位置は(25, 57121, 1)、半径はフレーム*2-3に変更しています。


これでばっちり、うまくいきました!
最後の10桁は9833673187になっており、

円周率の値を公開しているページなどを参照して確かめると最後の3桁以外はあっていそうです。

最後の3桁が間違っているのは、ポイントが有限個であり計算に使う桁を途中で打ち切っていることで本来行われるべきだった繰り上がり/繰り下がり処理が行われないことによる誤差の蓄積だと考えられます。
これは求めたい桁数より少し多めに計算することで事実上解決できます。
オーバーフローに注意!
先に述べたように、Geometry Nodesではfloatを使用して計算している都合上、計算途中で16,777,215を超える値が現れると正確な計算ができなくなります。
今回の実装でボトルネックとなるのは「積和算」ノードです。

まず、ベクトル演算の方ですが、直前にある「ラップ」ノードの出力は最大で57,120の値、「位置」ノードの出力は最大99の値をとる可能性があります。
すなわち、積和算ノードは最大で5,712,099(=57,120*100+99)の値をとり、これは16,777,215よりも小さいため、セーフです。
しかしもし、2桁ずつではなく3桁ずつ処理していた場合は最大で57,120,999(=57,120*1000+999)の値をとることになり、これは16,777,216を超えてしまうためアウトです。
今回円周率を2桁ずつ計算していたのはこれが理由です。
また、数式ノードの方の積和算にも十分注意する必要があります。直前にある「ラップ」ノードの出力は最大でフレーム数*2-4であり、「半径」ノードの最大値は396(=99*4)です。
すなわち、おおよそフレーム数が16,777,215の200分の1、つまり約8.3万フレームを超えるともう正確な計算ができません。
これはより多くの桁数を計算しようとした際に踏む可能性があります。
具体的には今回の目標である10000桁のための計算であればセーフですが、もっと桁数が多くなるとアウトである可能性がでてきます。
こちらは収束が速ければ速いほどオーバーフローまで余裕ができることになります。
収束は、使用している$${\arctan}$$の引数の分母のうち最も小さい値が大きいほど高速です。
例えば今回の分母は5と239なので、ボトルネックなのは5です。5がもっと大きい値であればもっと収束が速まります。
しかしその上で、先程述べたベクトルの方のオーバーフローにも注意する必要があり、つまりこれがオーバーフローしないギリギリを狙いつつ、分母の最小値をなるべく大きくしたいです。
ガウスの公式
今回、$${\arctan}$$の計算を三次元ベクトルを用いて計算していますが、Zの値は今のところ未使用でした。
つまり$${\arctan}$$項はもうひとつ分増える余裕があります。
$${\arctan}$$の分解を適切に行い、3項に分けつつ、分母の最小値を5より多くすることができるでしょうか?
結論から言うと、この条件のもと探索すると以下の式(ガウスの公式)が最適であることがわかります。
$$
\arctan 1 = 12 \arctan \frac1{18} + 8 \arctan \frac1{57} - 5 \arctan \frac1{239}
$$
分母の最小値は18であり、マチンの公式の5よりも大きく、有利です。
10000桁求める
では、満を持してポイント数を5005に増やし、Divideグループも5000以上のものを増やして円周率を10000桁求めていきます。
実行する場合は、数十分~数時間程度処理に時間がかかる可能性があることに注意してください。
参考までに筆者の環境(CPU : Ryzen 7 7700X)では22分22秒かかりました。


うまくいっていそうです。よかった。
おわりに
円周率はなかなかいい感じの題材ですね。
ここで紹介したものよりもっと高速なアルゴリズムは存在するので、ぜひ皆さんもチャレンジしてみてください。
GeometryNodesで変なもの作るのはこれ以外にもいくつかやっています。
この記事が面白いと思ったら、きっと他の記事も面白いと思ってもらえると思うので、是非どうぞ
参考文献
円周率.jp
円周率の値そのものや、arctan系公式について、かなり参考になりました。
超高速!多倍長整数の計算手法
多倍長な演算に関して、かなり参考になりました。
arctan 関係式一覧
効率的な公式を見つけるのに、かなり参考になりました。
この記事が気に入ったらサポートをしてみませんか?
