私たちの視覚には、目の構造ばかりではなく脳の働きも関わっているらしい。それで、いろいろな錯視が起こるという。
下図は最も単純なもので、同じ長さのA,Bでも、「B（上下）が長く見える」という錯視の例である。

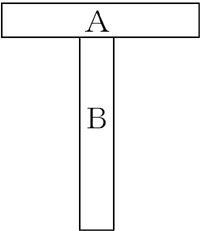
＜錯視ではないが・・・＞
 ここでは「錯視」ではないが、視覚が陥りやすい傾向性について考える。
それは、形を捉える時に「面積や体積に重点が置かれる」ということで、「輪郭線の長さ」は軽視されがちである、ということである。
私たちは「山」を見る時に、稜線の美しさに感動しつつも、その山の「ボリューム」に圧倒されることが多い。そして、「ボリューム」の中身は形であり、面積や体積に還元される。
 
手元に見える正方形や円、球などの図形では、「周の長さ」、「面積」、「体積」の大きさに優劣はなく、同等に扱われる。
ところが、場合によって、視覚が「周の長さ」を軽視することがある。
「周の長さ」を少なく見積もるのである。
それで、実際に計算をしてみて驚く。
それから、図形を見直すと「ストンと納得」したりする。

＜周の長さ＞
例えば、次図は一辺が十センチの正方形の中に三個の正方形が描かれている。この三個の正方形の「周の長さの和」はいくらになるのか。

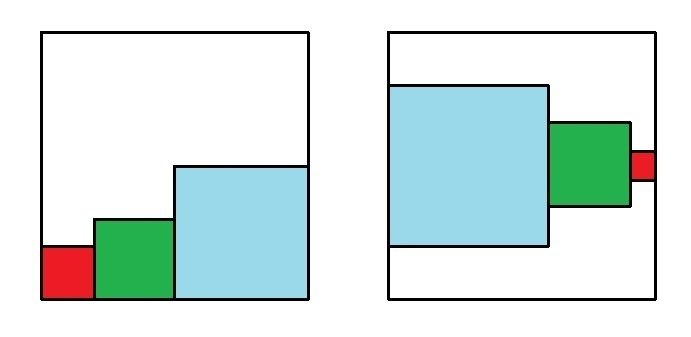
三個の正方形が合体した図形は、大きな正方形の一部分を占めているに過ぎない。大きな正方形より、面積は少ないのだから「周の長さ」も少ないはず！と脳は考えるらしい。
 
ところが、赤、緑、青の正方形の一片の長さを、それぞれ「２、３、５」として計算をしてみるとよい。
外側の大きな正方形の「周の長さ」に等しいことが分かる。
 
同様なことは「円周」でも起こる。
一辺が十センチの正方形に内接する円の周の長さは「10π」であり、正方形の周より小さい。その割合は「π/4≒0.785」である。

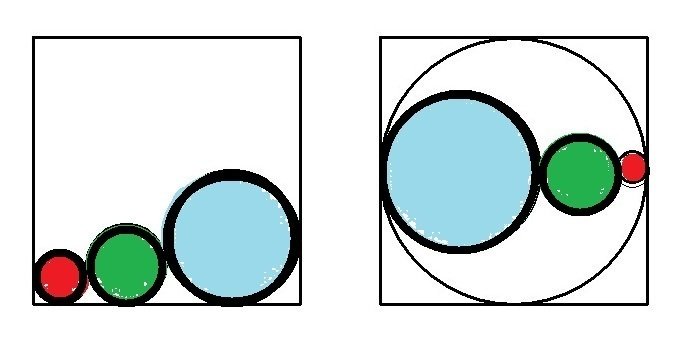
さて、赤、緑、青の円周の和はいくらになるだろうか。
それぞれの直径を「２、３、５」として計算すると「10π」になることは明らかである。

＜空から地上を観る視覚＞
視覚は机上の平面図形において、いつも正常で正確とは限らない。まして、地図のような平面図形を地上絵として風景に重ねる場合はなおさらである。
 
ところで、ヒトの想像力には限りがない。そして、その想像力は五感が感じたものとして表現される。
例えば、音楽家にとっては聴覚が中心になる。しかし、全ての想像力は視覚に関連しているように思う。音楽家の想像力も音で表現された後には「花が咲き春のような」などと視覚的に解説される。
 
今では、ドローンやヘリコプター、衛星が私たちの視覚を「空から地上を観る」ことができるように広げてくれる。
しかし、ドローンやヘリコプター、衛星が無い遠い時代から私たちの視覚は想像力によって限りなく広がっていた。「ナスカの地上絵」は分かり易い証拠である。

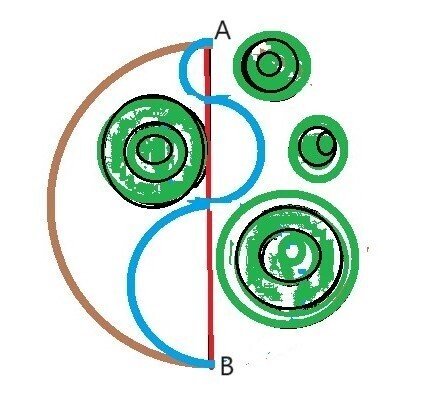
私たちが空から地上を観た時の風景を模式的に示すと上図のようになる。
Ａ点は水源地であり、Ｂ点は河口地である。
ＡからＢまでの直線距離は十キロメートルである。
緑色の二重円、三重円は山であり、ＡからＢまでの陸路は迂回するために茶色の半円となる。
陸路は「5π」キロメートルとなる。
この時、水源地Ａから河口地Ｂまでの青色の河川の長さはいくらになるのか。

＜想像力が視覚を広げる＞
想像力には限りがない。前述の「赤、緑、青の三個の円周の和」が外側の円周の長さに等しい、という平面図形の事実は、「無数の大小の円周の和」に広がり、実際の風景の中にまで広がる。

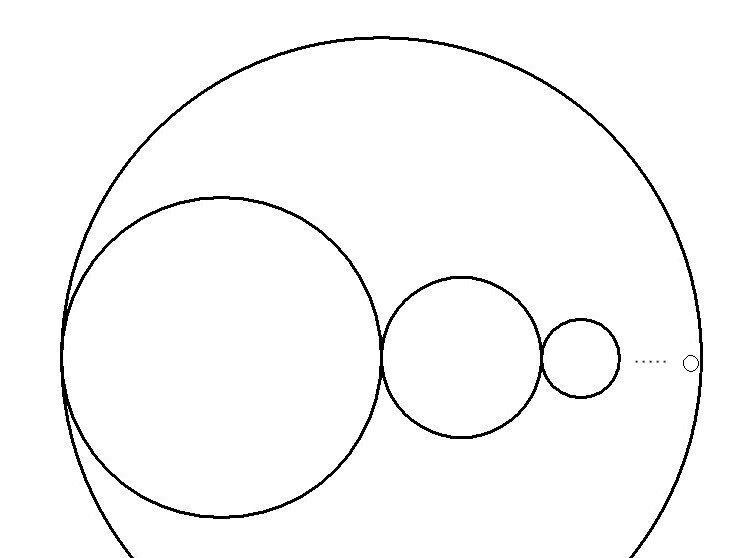
半径が「１」「１／２」「１／４」「１／８」・・・と無限に続く円の連鎖の直径の合計は「２」であり、無限個の円周和は外側の半径１の円周の長さに等しいことになる。（下の無限級数の和は「２」である。）

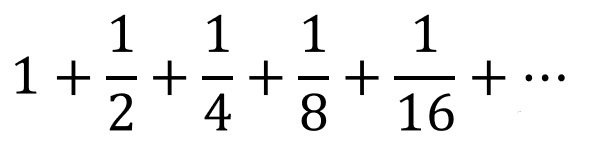
＜ステルムの定理＞
 また、ケンブリッジ大学の地球科学者ハンス・ヘンリック・ステルムは「河川の長さ」について次のような主張をする。
→「水源地から河口までの直線距離を直径とする円周の半分にほぼ等しい」
 
このことを「カオス理論」と観測によって証明したという。
「カオス理論」という言葉は、１９６１年に気象学者エドワード・ローレンツ（１９１７～２００８）が論文で用いたことに始まるという。
そして、「カオス」の特徴は「初期条件に大きく依存する現象」だという。
 
まずは、ステルムの主張に基づいて「多摩川の長さ」について検証してみたい。

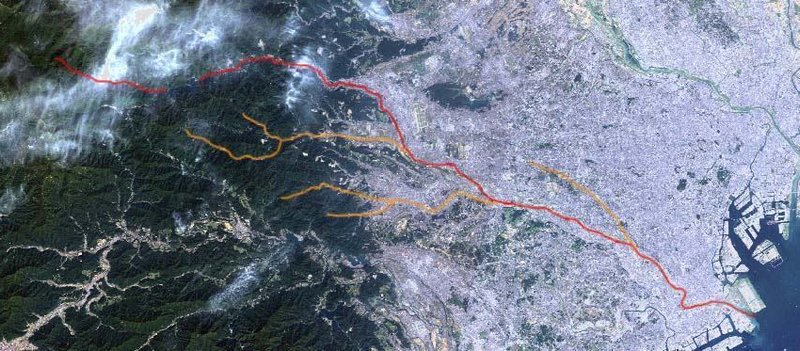
 多摩川は「笠取山（１９５３ｍ）」を水源地として、川崎浮島町付近が河口となる。それで、「Google Earth Pro」を用いて直線距離を測定してみる。
結果は「約９０km」である。（上図は多摩川の衛星写真）

ステルムの主張に従えば、多摩川の長さは「90×π÷2＝141.3km」ということになる。 
この長さは国土地理院の資料によれば「多摩川：138km」であるから、かなりの妥当性があることになる。
 
筆者は多摩川以外の河川についてもステルムの主張を検証している。
その結果として、河川が長ければ長いほどステルムの主張には妥当性が高い印象を得ている。
 
なお、「π÷2≒1.57」を直線距離に掛けることで河川の長さが求められることになるので、この「1.57」を「ステルムの河川定数」と呼ぶことにする。
 
＜初期条件に依存＞
宮城県に鳴瀬川という一級河川がある。水源地は「船形山（１５００ｍ）」で、野蒜海岸が河口となる。
直線距離を測定してみると「約54km」である。
それで、「河川定数」を掛けると、鳴瀬川の長さは「84.78km」と予想される。
国土地理院の資料によれば「鳴瀬川：89km」である。誤差は「5%」未満に収まるのではないか。

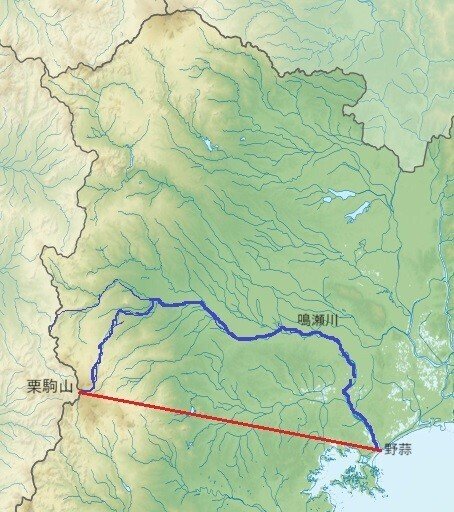
「誤差」は「初期条件に大きく左右されるカオス」の特徴でもある。
船形山からの一滴は河口の「東」には向かわず、「北」に向かって流れている。そして、小石の間を流れ、岩を超え、低地をさがして半円弧を描くように迂回しながら河口に向かっている。

＜フラクタル（自己相似）＞
 ところで、ステルムの主張は「カオス理論」に関係するばかりではない。「円の中の小さい円」や「正方形の中の小さい正方形」は「自己相似図」であり「フラクタル理論」の領域にも属している。
もう一度、「自己相似図」に戻って「自然」や「美」について考えることにする。

＜正三角形のフラクタル図＞
 まずは、「正三角形」について、外側の正三角形の周長と同じになる下図のような小さな「三個の正三角形」の図から描いてみる。

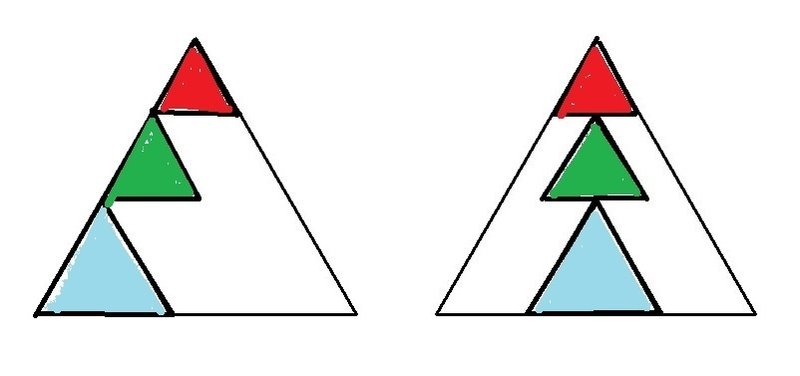
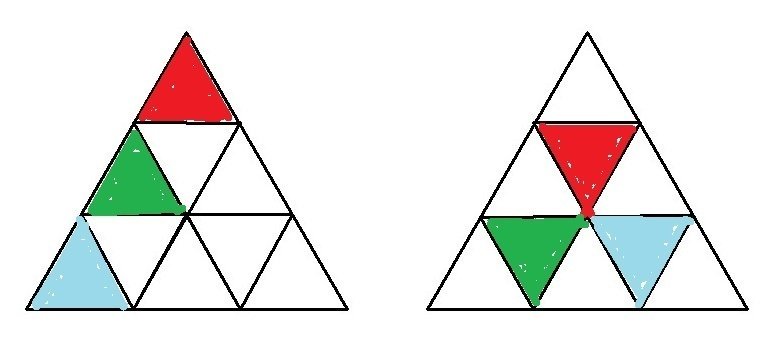
＜コッホ雪片＞
 次に、「コッホ雪片」と呼ばれる「自己相似図」を紹介する。
下図は正三角形の各辺を三等分して、点線で示した中央部分を「六十度回転」したのが黒太線分で、赤い線分を新たに加えたものである。

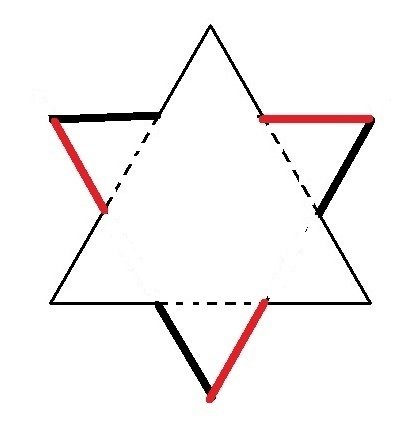
この変形によって、正三角形は星形になり、「自己相似性」が増したことになる。

最初の正三角形の一辺の長さを「１」とすると、「周長」は「３」である。それが、この変形によって、「周長は４」になる。
（三本の赤い線分の合計は「１」である。）
面積も最初の「√3/4」より「1/3」だけ増加する。
 
スウェーデンの数学者、ヘルゲ・フォン・コッホ（１８７０～１９２４）は、正三角形から始める「このような変形」を限りなく続けることで不思議なフラクタル図形を示した。

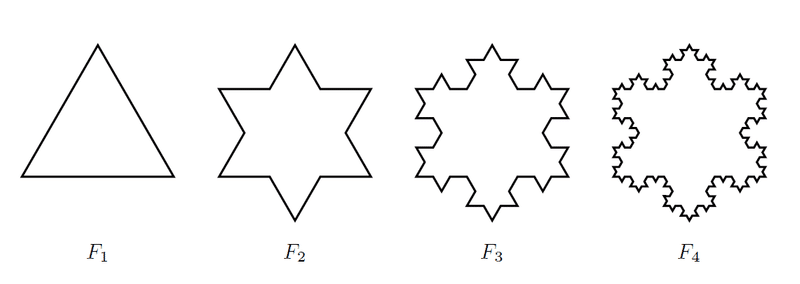
この図形は自然界にある美しい雪の結晶に似ている。
なお、このフラクタル図形の「周長は無限」で、面積は有限な「2√3/5」である。
私たちの視覚はどこまで納得し、追えるだろうか。