この記事はSmaart v.8 UserGuide Chapter1の一部を和訳したものです。
FIRフィルタの記事の基本事項を補完しつつ，基本的な知識の解説のために記載しています。

Chapter1:Fundamental Concepts and Terminology

用途にもよりますが，Smaartの運用に際して，幅広いシステム測定のコンセプトとプロオーディオを理解することが必要です。そのすべてを網羅することは本書の対象外ですが，この章ではSmaart v.8の操作とその応用を理解する上で大きな助けとなる，いくつかの重要な概念を紹介します。これらの概念や，音響測定およびサウンドシステムエンジニアリングに関するその他のトピックの知識を深めたい方は，原著171ページの「付録A：規格と参考文献」にある参考文献リストを参照してください。

Time and Frequency Domain Analysis(時間領域，周波数領域解析)

Smaartを活用するためには，時間領域解析と周波数領域解析の長所と違いについて理解することが重要です。信号やシステム応答を解析するプロセスにおいて，複数の視点から解析することは非常に有効です。Smaartの各主要動作モード(リアルタイムモードおよびインパルス応答モード)には，時間領域と周波数領域の両方の測定および解析機能が含まれています。

グラフや信号の"領域"とは独立した変数のことで，通常はグラフの横軸に表示されます。例えば，音声波形は時間領域の信号であり，信号のアナログ電圧またはデジタル振幅が時間と共に変化します。この場合，時間が独立変数となるので，通常，波形グラフの（横）X軸に時間，（縦）Y軸に振幅が表示されます。

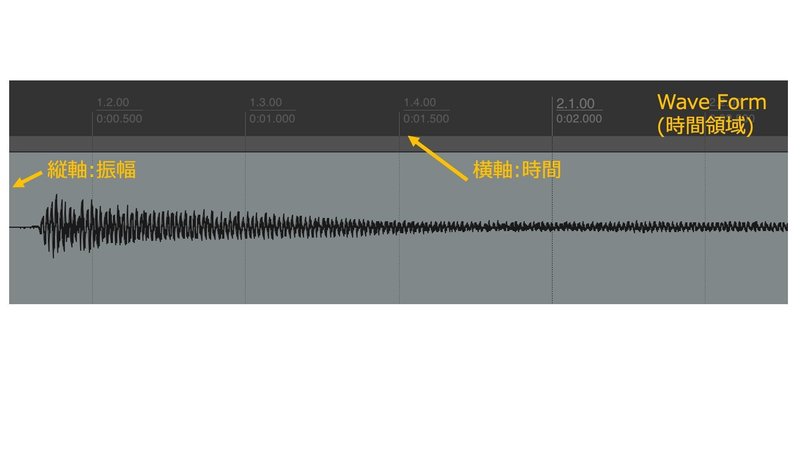
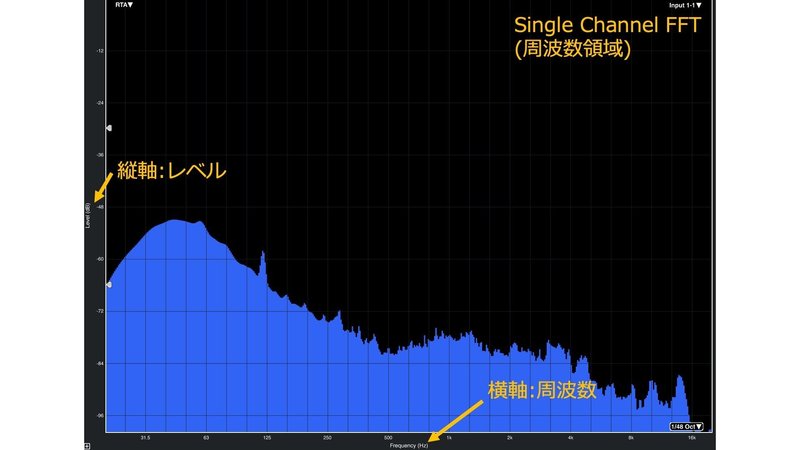
一方周波数領域のグラフでは，通常，X軸に周波数，Y軸にマグニチュードをとります。

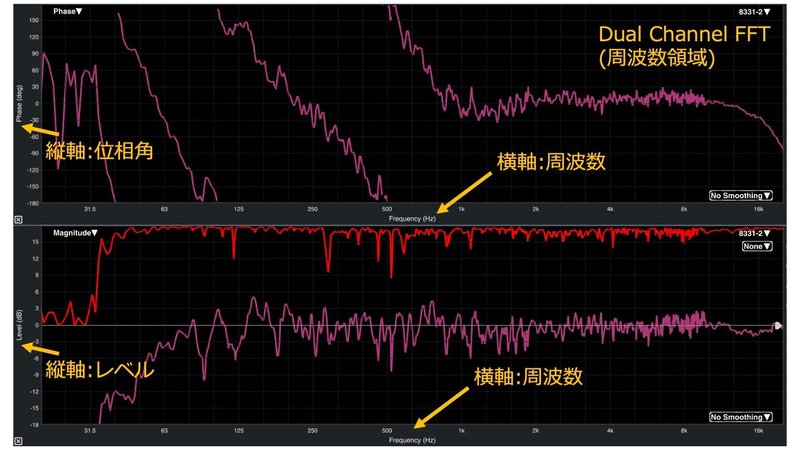
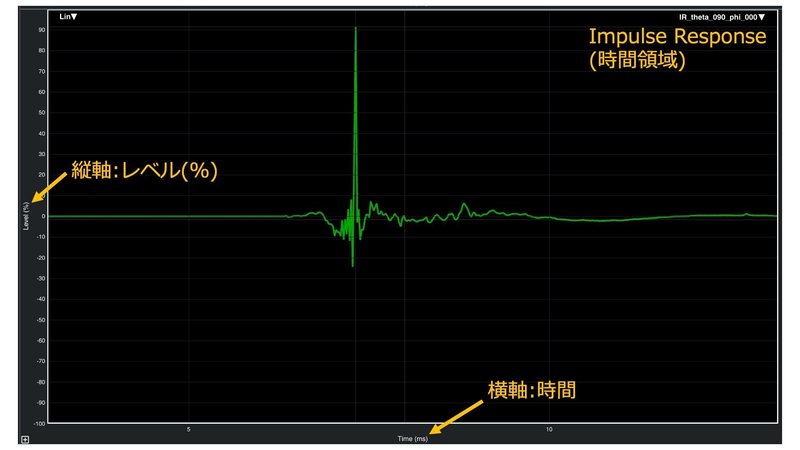
ただし、スペクトログラフは例外で，時間と周波数の2つの独立した変数があるので，その状況に応じて最も理にかなった方向に配置します。

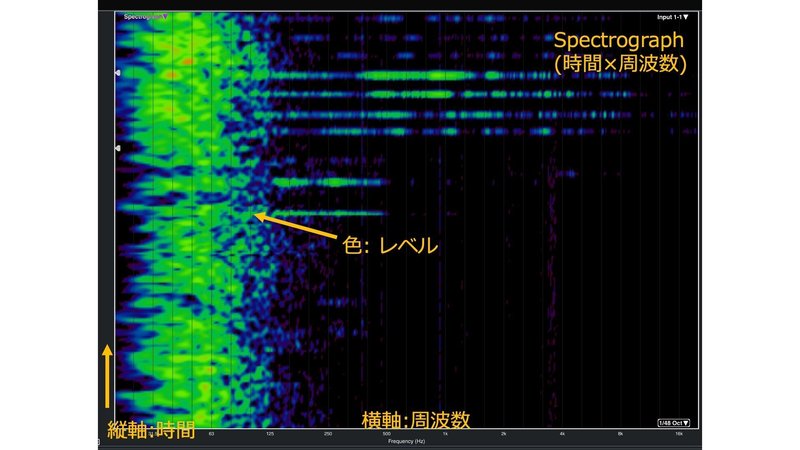
レコーディング用途では，音声信号の時間領域グラフはサウンドエディターにとって重要な波形表示となります。一方音響工学や室内音響学では，システムの応答(インパルス応答)を時間領域で見ることにより，システムの遅延や，問題となりうる反射音や残響がわかります。

信号の周波数領域分析では，そのスペクトルを見ることができます。これは明らかに音色の分析やフィードバックしている周波数を探す際に非常に有用です。システム応答(伝達関数または周波数応答)の周波数領域表示は，システムの振幅特性と周波数ごとの時間/位相特性について有用な情報を提供します。

原著内 Fig.1はシステムの応答を調べるために，時間領域と周波数領域の両方の表示を利用することの利点を示す非常に良い例です。周波数応答測定では,
振幅特性でディップやピークを持つ応答が描かれています(右下)。しかしこれは問題が可視化されているのみで，実際の原因は別にありそれはここからは見えません。リップルの原因は，システム応答の時間領域表示でインパルス応答を見ることで直接音以後の顕著な反射が原因とわかります。反射は直接音が何らかの表面で跳ね返された後，時間的に遅れて到着するものです。同じ信号(相関のある信号)2つが時間差(一定時間以内)をもって到来したものを周波数領域で見ると，コムフィルタ(櫛形フィルタ)になります。

Fourier Transforms(フーリエ変換)

フーリエ変換は19世紀のフランスの数学者であり物理学者であるJean-Baptiste Joseph Fourierにちなんで名付けられたもので，音声や音楽などの複雑な信号は，振幅と位相の関係が異なる正弦波から構築できる，あるいは正弦波に分解できるという考え*に基づいています。フーリエ変換は時間領域の信号のスペクトル構成を見るためにオーディオ分析に広く使用されています。逆フーリエ変換はスペクトルデータから時間領域の信号を再構成**します。

フーリエ変換にはいくつかの種類がありますが，Smaartで扱うのは離散フーリエ変換（DFT）で，有限長の時間領域の信号に対して機能します。一般によく言われる高速フーリエ変換（FFT）は，DFTをより効率的に計算する方法を指し，最も一般的には，分析する信号のブロックが4096($${4K = 2^{12}}$$)，8192($${8K=2^{13}}$$)，16384($${16K=2^{14}}$$)...など，2の冪乗($${2^n}$$)のサンプル長であることを必要とします。(実はこれに限らず高速に実行が可能です。)すべてのFFTはDFTに基づくものであり計算結果は同一のものが得られますが，すべてのDFTが高速であるとは限りません。

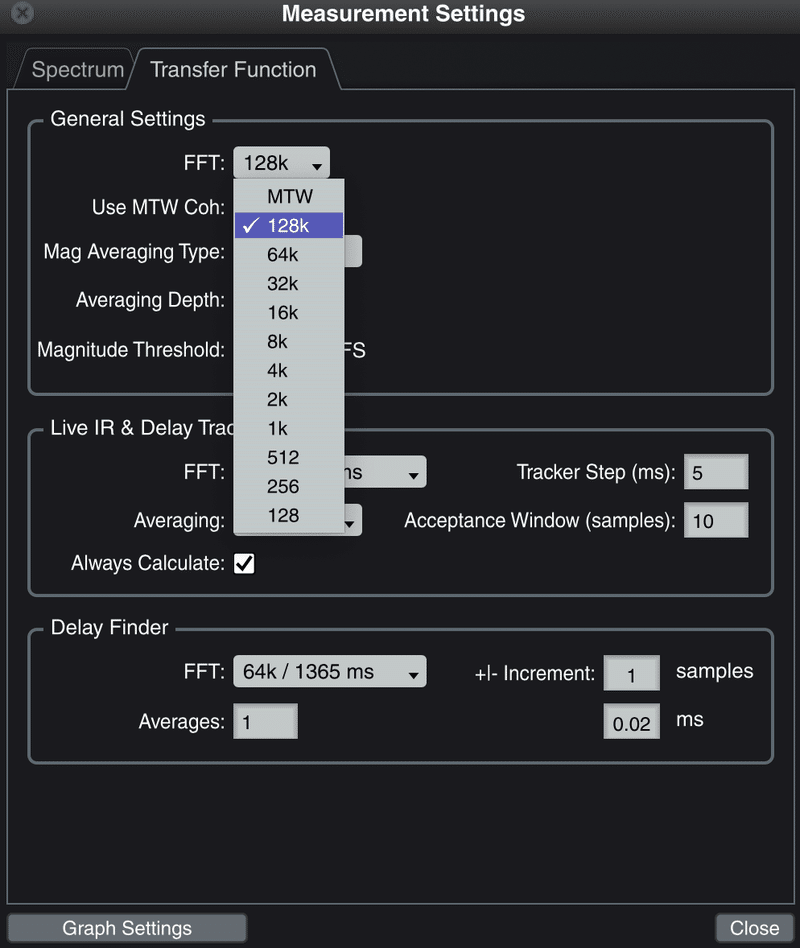
SmaartのほとんどのDFTは2の冪乗FFTです。2の冪乗以外に任意の長さの信号に対してDFTもできますが，一般にFFTの方が高速に処理できる***ため，特にリアルタイム処理，あるいはそれに伴う時刻に関する制約が問題にならないようなアプリケーションではFFTが非常に好まれます。

*これらはフーリエ級数展開と呼ばれる手法に基づいています。フーリエ級数展開は直交関数展開と呼ばれる手法に基づくもので，$${\sin\theta}$$と$${\cos\theta}$$を基底として，それらに係数をかけた線形和である信号を表そうというものです。関数展開は理工学系の大学学部一年で必ず習うテイラー展開をイメージするとわかりやすいでしょう。テイラー展開はxの冪乗で任意の関数を展開しますが，フーリエ級数展開は周期の異なる$${\sin\theta}$$や$${\cos\theta}$$(=異なる周波数の正弦波)で展開をします。

**ある関数をフーリエ変換して逆フーリエ変換をすると元の関数に戻ります。

***FFTによく採用されているCooley-Tukeyアルゴリズムのうち，Radix-2の場合は2の冪乗の信号長を必要とします。そのため，任意の長さの信号に対しては，2の冪乗になるように音声信号の末尾に0を詰めることがあります。一方このRadixは2に限らないため，実は(素数でない限りは)2の冪乗に限らずとも高速化が可能です。

Time Resolution vs. Frequency Resolution(時間分解能と周波数分解能)

この章についてはいくつかミスリーディングな表現があるため，意図的に表記を変えています。周波数分解能についてはDFTについても同様のことが言えますが，一般にDFTを行う場合はある程度信号長が取れる場合もあるため，STFTの話へ変えています。

離散フーリエ変換(DFTまたはFFT)をリアルタイムに使用するためには，入力信号を一定ブロックで区切りながら逐次的にDFT/FFTを行う短時間フーリエ変換(STFT)が必要になります。STFTを使用する際の重要な性質は，時間分解能と周波数分解能のトレードオフであり，一方が良くなれば他方は悪くなります。どちらも測定の「時間窓長」の関数になります。時間窓長とは，あるサンプリングレートで，あるサイズのDFTを行うために必要なサンプルを記録するのにかかる時間のことです。時間窓が長いとよりタイトで詳細な周波数分解能が得られますが(高周波数ではしばしば過大になります)，その分時間分解能が低下します。(たとえば入力信号を長いブロックで取り込めばより詳細な周波数分解能=低域まで扱えるようになりますが，長いブロックで区切ると短時間での音の変化が埋もれてしまいます)

ピンクノイズのような統計的にランダムな信号を用いて，信号の長期間の平均やサウンドシステムの定常状態を測定する場合には時間分解能はあまり気にならないかもしれません。しかし，音声や音楽のようなダイナミックな信号を分析する場合，非常に近い時間間隔で存在する信号の特徴を個別のイベントとして見る必要がある場合には，時間分解能は重要な要素となります。例えば，1回のFFTの時間窓内に2つのドラムのビートが発生した場合，周波数領域での結果のスペクトルには，それぞれの周波数で両方のエネルギーが1つの数値として含まれてしまいます。各ビートを個別のイベントとして見る必要がある場合は時間窓を短くする必要があり，その結果周波数ビンの間隔(=周波数解像度)が広くなってしまいます。

STFTの必要な時間窓長(秒)は，時間領域信号の記録に使用したサンプリングレートを使用したいFFTサイズ(サンプル数)で割ることで算出できます。例えばSmaartのスペクトル測定におけるデフォルトのFFTサイズは16K(16384)サンプルです。48000サンプル/sで記録された16K FFTの時間窓長は0.341秒(16384/48000)，つまり341ミリ秒となります。

$$
Time Constant = \frac{FFT Size} {Sample Rate} = \frac{1} {Frequency Resolution}
$$

低周波数は高周波数よりも周期が長いので，それを解決するために長い時間にわたって信号を取り込まなければならないのは自明です。実際STFTで「見る」ことのできる最低周波数は1/Tで，TはFFTの時間窓長(単位は秒)です。サンプルレート48kの16K FFTの例では，周波数分解能は2.93Hz（1/0.341）となります。

$$
Frequency Resolution = \frac{Sample Rate }{FFT Size} = \frac{1}{Time Constant}
$$

正弦波における周期と周波数の逆数関係(f = 1/T，T = 1/f)をご存知の方なら
STFTの時間窓長と周波数分解能の関係と同じであることにお気づきでしょう。実際，STFTの周波数分解能は時間窓内でちょうど1回だけ循環する正弦波の周波数に等しくなります。他のすべての周波数ビンはこの基本周波数の整数倍(高調波)であり，時定数を知ることは周波数ビンの間隔を知ることでもあります。

実用的にはサンプリングレートが44.1kHzまたは48kHzの場合，Smaartのスペクトル測定用のデフォルトFFTサイズである16Kは，サブウーファー周波数帯の下限までの非常に優れた低周波分解能と，ピンクノイズなどの信号分析に必要とされるよりはるかに大きな時間分解能を提供します。音声や音楽などよりダイナミックな信号の場合，サンプリングレート48kHz，16K FFTで1分間記録すると，1分間に176フレーム(60 / 0.341 ≒ 176)程度となります。これはほとんどの音楽ジャンルの平均的なテンポと同じかそれ以上であり，ほとんどの場合個々の音のスペクトルの内容を確認するのに十分な時間分解能であると考えられます。
音声分析の場合，英語のネイティブスピーカーの一般的な会話速度は1分間に140～180ワード，200～300音節程度なので，16K FFTではワード数は得られても音節数は得られません。FFTサイズを8Kに落とすと時間分解能は2倍の約352フレーム/秒になり，ハイテンポな音楽に対応したり一般的な会話速度で個々の音節を聞き分けるには十分ですが，低周波数の解像度が多少犠牲になります。

時間窓長に関連する他の問題点として，サイズが大きくなると指数関数的に増加する計算コストと，リニア間隔で取られるDFTデータを対数周波数スケールで表示したときに高周波数では過剰な周波数分解能になる問題があります。RTA測定では1/Nオクターブバンドフィルタを使用することで，高周波数の過剰な分解能の問題を解消し，ローエンドなコンピュータでも16Kや32KのFFTサイズを使用してリアルタイム分析を比較的容易に実行できます。

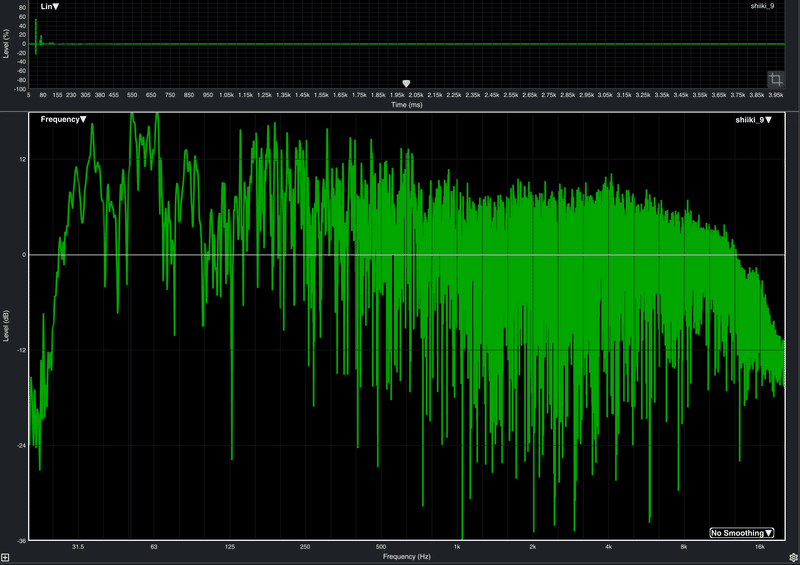
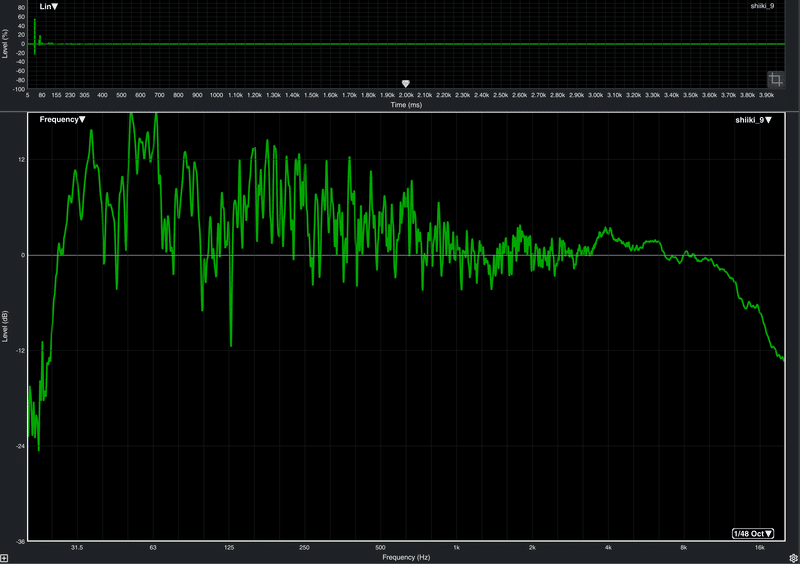
一般的に計算コストがより大きな問題となる伝達関数測定において，Smaartのマルチタイムウィンドウ(MTW)機能は，高周波数で過剰に高い分解能を発生させずに低周波数で約1Hzの分解能を実現するために，低周波数にいくにつれて徐々に低いサンプリングレートと小さなFFTサイズを使用し，周波数分解能と計算量の問題を解決しています。また伝達関数をスムージングすることで高周波数での過剰な分解能を解消することができます。スムージングはMTWと単一のFFTサイズを使用する測定の両方で使用可能です。

Single and Dual-Channel Measurement Techniques(シングルチャンネル/デュアルチャンネル測定手法)

Smaartのリアルタイムモードでは，シングルチャンネル(信号解析)とデュアルチャンネル(応答解析)という2種類領域での基本的な測定が行えます。シングルチャネルのスペクトル測定は信号の周波数成分と振幅しか分からないため信号解析測定となります。リアルタイムスペクトラムアナライザ(RTA)とスペクトログラフの表示はシングルチャンネルのFFT分析に基づいています。

他の例としては、音圧レベル(SPL)や等価騒音レベル($${L_{\mathrm{eq}}}$$)などのサウンドレベル測定が挙げられます。SPLのように絶対的な基準に対して校正された場合，シングルチャンネル測定は他の絶対値と直接比較可能な物理量を得ることができ，ある周波数またはある周波数範囲における音の大きさを正確に教えてくれます。この測定では，"その信号にはどれだけの1kHzのエネルギーが含まれているか"，"その音の周波数は何か"，"会場のこの場所でのSPLはどうか "といった分析に役立ちます。

デュアルチャンネル測定は，直感的には2つの信号を比較してその類似点と相違点を見つけます。Smaartの伝達関数測定とインパルス応答測定はデバイスやシステムの出力とそれを生成した入力信号とを比較するデュアルチャンネル測定です。入力に対するシステムの応答を測定していると言えます。また2つの信号の時間的関係を正確に測定できるため，位相を調べたり遅延時間を求めたりすることも可能です。

デュアルチャンネル測定は相対的な分析(入力対出力)を行い，「システムのクロスオーバー周波数はどのくらいか」，「1 kHz でのブーストまたは減衰はどのくらいか」，「メインシステムからのエネルギーはいつ測定マイクに到達するか」といった分析に役立ちます。
シングルチャンネル測定とデュアルチャンネル測定は，それぞれの長所と短所，つまり何を測定しているのか/何を測定していないのかを理解すれば，どちらも強力なツールとなります。しかしこの2つを混同すると，不完全または不正確な情報に基づいて誤った判断を下してしまうことになりかねません。

LinearとLog

音響解析で繰り返し遭遇する問題のひとつに，人間の知覚が対数的な性質を持ち，比較的大きな値の範囲をカバーすることが挙げられます(Weber-Fechnerの法則)。聴力は人それぞれですが，一般的に聴覚の閾値と痛みの閾値，つまり私たちが聞き取れる最も小さな音と耐えられる最も大きな音の差は，およそ120 dB程度と言われています。これは小数点以下6桁(例えば、1と100万の差)の計算になります。

周波数で言えば，人間の可聴域は一般的に20Hzから20kHzと定義されており，これは10を底にとった対数(常用対数)で言うと4(真数的には$${10^4}$$)の範囲にあたります。ほとんどの人はその範囲全体を聞き取ることはできませんが，ほとんどの人は少なくとも真数的には$${10^3}$$の範囲，例えば80Hzから8kHzの範囲を聞き取ることができると言ってもいいでしょう。これはかなり広い数値です。
つまり私たちはすべての物理現象の数値の違いを等しく聞き分けているわけではないのです。私たちの感覚では，物理現象の数値での1と2の違いは世界を直線的に(Linearで)認識した場合の2と3の違いとは同じではありません。1と2の違いは，2と4，4と8，8と16...の違いに聞こえる(見える、感じる)のです。

オーディオや音響データを対数の振幅スケール(レベル)や周波数スケールで表示することは，私たちにとって2つの有用なことがあります。それは私たちの聴覚が包含する幅広い値の範囲をより扱いやすくし，人間の知覚という観点からより意味のあるデータの表示になることが多いということです。Linearスケールが使えないというわけではありませんが，Smaartで行うほとんどの作業ではLogスケールと単位(オクターブ、デシベル)の方が直感的に理解できる方法で見たいものを示すのに適している傾向があります。

LinearとLogの周波数軸

リニア周波数スケールと対数周波数スケール(1/nオクターブバンドではない)については，チャートやグラフにどのように周波数が実際にプロットされるかについて話しているだけです。リニア周波数スケールでは，例えば100ヘルツごとに(数字はいくつでも選べます)グラフ上で他の周波数と同じスペースを占めます。オクターブスケールでは各帯域の線形周波数範囲は周波数が上がるにつれて倍増するにもかかわらず，各オクターブは他のオクターブと同じ幅で表示されます(125 Hz，250 Hz，500 Hz，1 kHz，2 kHz，4 kHz...)。対数周波数スケールでは，10Hzの各乗数(10，100，1000，10000)は，それぞれ同じ幅になります。対数スケールはどの底でも同じように機能しますが，Smaartで対数スケールに使う底は2と10です。

オクターブや底10の対数スケールで周波数を見ることが多いのは，これらのスケールの方が私たち自身の対数的な音の感じ方とよく相関しているからです。しかしリニアスケールも非常に有用な場合があり，音や音響の基礎となる物理学との相関が高い場合もあります。リニアスケールで周波数をチャート化するとローブやピークが直線的な間隔になるため，コムフィルタや高調波歪みがよりはっきりと目立つようになります。別の例としては遅延に伴う位相シフトが考えられます。
音響測定やその他のノイズの多い信号のFFTデータを対数周波数スケールで見ると，周波数が高くなるにつれてトレースがぼやけて見えることに注意してください。これは必ずしも高周波数にノイズが多いという意味ではありません。これはより多くのFFTポイントをより小さなグラフスペースに詰め込むことによる自然な結果です。これが先に述べたMTW伝達関数オプションの理由のひとつです。スムージングはスペクトラム測定における1/nオクターブバンディングと同様に伝達関数測定における高周波の"視覚的ノイズ"を低減するのに役立ちます。

リニアでのMagnitude表示

リニア振幅とは，その名の通り振幅をリニアスケール，例えばボルトやデジタル整数ベースの振幅単位で表示したものです。Smaartではリニア振幅が表示されるのはリニア時間領域グラフのみで，振幅は正規化されたフルスケールに対するパーセンテージで表示されます。つまり与えられたビット数の符号付き整数(サンプルあたり16ビットや24ビットなど)から得られる最大の正負の数値は1から-1の範囲にスケーリングされ，その間の端数値はパーセントで表示されます。

負の数の対数を取ることはできないため(真数条件)，インパルス応答の相対的な極性を見る唯一の方法は線形振幅スケールを使用することです。また、インパルス応答内の不連続な反射を特定するためにリニア振幅スケールを好む人もいます。リニア振幅スケールは，残響減衰を見たり，波形の周期が時間的に大きく広がっていて明確なインパルスが容易に識別できないインパルス応答の低周波数のピーク構造を識別したりするのにはあまり役に立たない傾向があります。

dB

デシベルは，振幅，電圧，音圧，利得，減衰などさまざまなものを表現するためによく使われる対数比です。文字通りBelの10分の1を意味します。Belは電話の発明者(の一人)であるアレクサンダー・グラハム・ベルにちなんで名付けらています。なぜ "Bell "ではなく "Bel "なのかは他の誰かが答えなければならない問題ですが，デシベルの略称がdB(大文字のB付き)と表記されるのはおそらくそのためでしょう。ほとんどの人は代わりに10dBと言うでしょうが，1 B(1ベル)が10:1の電力比の対数を表し，1デシベルがその1/10であることを考えれば，デシベルへの変換式やデシベルからの変換式はそれほど恣意的なものではないと思えるかもしれません。

$$
\mathrm{dB~(Power)} = 10 * \log_{10}(\mathrm{Power}) = 20 * \log_{10}(\mathrm{Amplitude})
$$

$$
\mathrm{Power} = 10^{\mathrm{dB} / 10} = \mathrm{Amplitude}^2
$$

$$
\mathrm{Amplitude} = 10^{\frac{\mathrm{dB}}{20}} = \sqrt{\mathrm{Power}}
$$

dBは比率を表すので，何かを基準にしなければなりません。前ページの式のように基準値が明示的に与えられていない場合は，基準値は1であると暗に仮定されます。基準値がある場合，対数をとる前にdBに変換したい値を基準値で割ることでdBを1以外の数値を基準にできます。

つまり，$${v}$$をdB表示したいリニアの値，$${v_0}$$を基準値とすると，以下のように表されます。

$$
\mathrm{dB} = 20*\log_{10}(\frac{v}{v_0})
$$

オーディオでよく使われる例としては dBuがあり，これは 0 dB(基準値)を 0.775 Vとしています。dB FS (dB Full Scale)は0 dBを0.5の平方根（0.7071）に変換するもので，フルスケール，peak to peakの正弦波の実効値は-3.01 dBではなく0 dBとなります。

オクターブバンド，1/nオクターブバンド

オクターブや1/nオクターブのバンドスペクトルは，アナライザ画面に表示される音と聴こえ方を一致させるもう一つの方法です。RTAやスペクトログラフの帯域表示では，各1/nオクターブ帯域はその帯域に含まれるすべての周波数のパワーの合計を表します。そのためピンクノイズの帯域測定は帯域表示では平坦に見えますが，リニアでのFFTデータを見ると1オクターブあたり3 dB，底10の対数バンドあたり10dBでロールオフする信号が表示されます。個々のFFT周波数ビンは周波数が上がるにつれてエネルギーが減っていきますが，各オクターブ帯域はリニアで2倍の幅の周波数で構成されているため，すべての帯域を足すと同じデシベル数になります(完全なピンクノイズの場合)。(少なくとも名目上は)すべての周波数でエネルギーが等しいホワイトノイズ信号を見ると，帯域なしの線形または対数周波数スペクトル表示では平坦に見えますが，オクターブバンド表示では1オクターブあたり3dBで上向きに傾斜していることがわかるでしょう。

バンドスペクトル表示はいくつかの理由で有用です。特にピンクノイズと併用することで，デバイスやシステムの周波数特性のマグニチュード部分のみの貧乏人的な測定を行うことができます。シングルチャンネルのスペクトラム測定では，到達時間や位相の関係(どちらもシステムが実際にどのように聞こえるかにおいて重要な要素である)については何も分かりませんが，ピンチの時や既にアラインメントが取られているシステムのクイック・メンテナンス・チェックとしては何もしないよりはマシでしょう。もう1つはスペクトルデータをスムージングする方法です。FFTで複数のビンを各バンドに合計することで，個々の周波数ビンのばらつきが大きいデータを見るよりも滑らかで安定した表示がすぐに得られるようになります。

バンドスペクトル表示には音響心理学的な側面もあります。ピンクノイズ，または物理学で1/fノイズと呼ばれるものは，自然界やあらゆる種類の複雑な系に偏在しているように思われています。したがって幅広いジャンルや文化にまたがるあらゆる種類の音楽の長期平均スペクトルが，ピンクノイズのそれと似ている傾向があることは驚くべきことではないかもしれません。そのため帯域スペクトル表示は，音楽やその他の信号のスペクトル内容を見る上で自然で直感的な方法となる傾向があります。

Transfer function機能でのSmoothing

伝達関数データの1/nオクターブ平滑化は，データの大きな特徴や傾向を見やすくするために振幅や位相の小さな変動をフィルタリングするのに便利です。これは1/nオクターブバンド処理と似ていますが，和をとる代わりに平均をとります。平滑化は1/nオクターブ間隔で固定数の帯域にビンを集めるのではなく，各周波数データポイントをそれぞれの "帯域"の中心に配置します。この場合各 "帯域"は周波数が上がるにつれて拡大する中心加重平滑化窓のことです。
対数表示では，リニアなFFTのデータポイントに対して，高周波数へ近づくにつれて平滑化窓が広くなり，平均に含まれる両側のポイントが増えます。これはノイズの多い信号のFFTベースの測定値を対数周波数スケールでプロットする際に特有の高周波の"ファジーさ"を抑えるのに役立ちます。

平均化

Smaartでは，ノイズや残響，位置に依存する音響的な異常などの外的要因から有用な情報を分離するために，さまざまな方法で平均化を行います。Smaartの平均化は時間的平均化と空間的平均化の2つに大別されます。

時間的平均化

時間平均とはある一定期間の測定を平均化することです。通常これは1つの測定ポイントまたはマイクロホンの位置で行われますが，特殊な用途では時間平均を利用した移動マイクロホン測定が用いられることもあります。音響測定では，測定しようとしている信号の中に様々な音源からのノイズが大量に混入します。ノイズ成分はランダムであり，入力される測定データの個々のフレームごとにかなり変動します。このためチャートは大きく飛び跳ね，ノイズが多く読みにくいものになりがちです。

時間をかけて平均化することは，平均への回帰というプロセスを通じて測定の信号対雑音比(SNR)を増加させます。入力データのノイズ部分は信号成分よりもランダムであるため，経時的に集計すると互いに相殺される傾向があります。信号成分は定常的な特徴(測定される信号が急激に変化しない定常システム測定の場合)であるか，少なくともノイズ部分よりもランダム性が低い(動的な信号を分析する場合)ため，それ自体は平均化されてより滑らかで見やすくなる傾向があります。

どちらの場合も応答性がトレードオフになります。ダイナミックな信号のスペクトルコンテンツを分析する場合，平均化しすぎると実際の信号の一部の見る必要のある揺らぎをマスクしてしまうことがあります。システム応答の測定では，過度の平均化はイコライゼーションやディレイの調整などシステム調整の変化に対する測定値の応答を遅くします。重要なことは必要十分な回数を使うことです。

電気的測定では通常ほとんど平均化せずに測定できます。音響測定では，必要な平均回数はバックグラウンドノイズレベルやユーザーの好みによって異なります。ノイズの多い環境で測定する際，システムのイコライゼーションとアラインメントを高速化するためにできることの 1 つは，設定を変更した後に [V] キーを押すことです。これによって平均化バッファがリセットされて平均化が再スタートするため，変更結果を確認する前に測定から最も古いデータが落ちるのを待つ必要がなくなります。

リアルタイム測定の時間平均は，メインウィンドウの右側にあるコントロールバーのAveraging コントロールから設定します(Fig. 10を参照)。平均化回数だけでなくタイプの組み合わせも利用可能です。

• リストの最初4つの選択肢は，直近の2/4/8/16フレームのデータの等加重単純移動平均(FIFO平均と呼ばれる)です。この手の平均手法では，新しいフレームが入ってくると最も古いフレームは完全に測定から外れるので，"First In, First Out "を意味する "FIFO "と呼ばれます。

• 1-10Secと表示されているオプションは，FIFOと指数移動平均の最も望ましい特性を組み合わせており，Smaart側が可変平均と呼ぶ独自の平均法となります。

• fastとslowは標準的な騒音計で使用されるfast指数時間積分とslow指数時間積分の減衰特性をモデル化したものです。これらはそれぞれ0.125秒と1.0秒の時定数を持つ一次指数平均です。

無限(Inf)平均は，区間を設定しない累積的な等加重平均です。測定を停止するか，[V] キーを押して再開するまで単純に平均を取り続けます。定常状態のシステムの応答を可能な限りきれいに取ったり，音声や音楽のような動的な信号の長期的な平均スペクトルを求めたりするために，必要であれば数分から数時間にわたって平均化することができます。

Polar平均化 vs. Complex平均化

伝達関数測定でのMagnitudeデータの時間的平均化には，Polar平均とComplex平均の2つのオプションがあります。Polar平均はDecibel平均とも呼ばれることがあります。これはまず入力される各フレームのデシベルの大きさを計算し，その結果の移動平均をとるからです。Complex平均は複素数の実数部と虚数部の2つの移動平均を保持し，バックエンドでこれらの平均からMagnitudeと位相を計算します。

Polar平均(RMS平均と呼ばれることも)は風，気流，機械的な動きなどの要因が存在する状況では，この2つのうちではより安定していてロバストな傾向にあります。Complex平均("ベクトル"平均とも呼ばれる)は一般的にノイズ除去に優れ，Polar平均化よりも残響エネルギーを除去する傾向にあります。

Smaart v.8の位相平均は常に複素数データに基づいています。RTA測定における時間平均では常に2乗Magnitude(パワー)を平均します。

主観的な観点では，Polar平均は残響エネルギーをより多く取り込む傾向があるため，2つのオプションのうちより"音楽的"かもしれません。Complex平均は主観的な音声明瞭度との相関がやや高くなる傾向があります。このオプションは各伝達関数の測定に対して個別に設定できるため，リアルタイムで比較し，ある状況において一方が他方よりも良い答えを出すかどうかを簡単に確認することができます。

空間的平均化

Smaartの空間平均は時間平均とほぼ同じように機能します。この場合，異なることは1つの測定地点で異なる時間に行われた測定値ではなく，異なる測定地点で行われた測定値を平均化することです。空間平均はシステム応答と1ヶ所における局所的な音響的異常とを分離したり，バックグラウンドノイズやラウドスピーカーからの全体的なカバレージをより広く統計的に把握したりするのに役立ちます。

複数のマイクと入力があれば，リアルタイムで空間平均を行うことができます。また異なる場所でキャプチャした測定スナップショットを保存して，平均化することもできます。ライブ測定の設定と保存されたデータスナップショットの操作については次のセクションで説明しています。以下のオプションはどちらの方法にも適用されます。

Power平均 vs. Decibel平均(RTA測定)

RTA測定では，Power平均とDecibel平均を選択できます。Power平均では分析対象の信号の平均的なパワースペクトルが得られ，バックグラウンドノイズ調査などの信号分析アプリケーションや，その他の理由で広い範囲の平均サウンドレベルをチェックする場合に一般的な選択となります。Power平均化では，各周波数で最も大きな音に重みが置かれるため，グラフは大きなPowerに引っ張られることになります。

Decibel平均はdBの大きさを単純に算術平均したもので，一般的な音響システムの測定に適しています。パワー平均よりも"コンセンサス"が得られると言えるかもしれません。例えばPower平均の測定値の1つが他のすべての測定値よりも著しく高いレベルになった場合，その測定値が平均値を支配することになり，カーブ全体の形状が大きく変わってしまう可能性があります。dB平均では，より高いレベルの測定値は，平均化された曲線全体のレベルをより高くしますが，平均への他の寄与よりもその形状に大きく影響しすぎるすることはありません。(筆者としては，この平均手法は物理的対応をなくすので注意が必要だと考えています。一般的にdBをとる場合でもリニアの値で平均をします。)

Coherence Weighting(相関による重みづけ)

伝達関数データの場合，MagnitudeデータにはDecibel平均が使用され，位相平均にはComplex平均が使用されます。ただしCoherence Weighting(コヒーレンスによる重み付け)を使用する(または使用しない)オプションがあります。Coherence Weightingは，各測定で最も高いコヒーレンス値を持つ周波数により多くの重みを平均に与えます。コヒーレンスは伝達関数の測定においてS/N 比の予測因子となる傾向があります。複数のマイクロホン位置からのデータを平均化する場合，ある測定が局所的な残響のためにいくつかの周波数でコヒーレンスが悪い場合，あるいはHFがローリングオフしているスピーカーのカバレージパターンの端の近くで測定された場合，コヒーレンスの重み付けはより信頼できる周波数が問題のある周波数よりも平均に寄与する結果になるでしょう。