さっそくですが2013年度武蔵中の問題を載せて解説をします。

（１）

つりあった時使うおもりの数を奇数と仮定します。奇数個のおもりを２つの皿にのせるとき、必ず片方は偶数でもう片方は奇数になります。一方、２回目以降の操作で使うおもりは必ず奇数ｇになっていますから、偶数個のせた方の皿は合計も偶数ｇ、奇数個のせた方の皿は合計が奇数ｇとなってこれらは必ず一致しないためつり合いません。奇数個でもつり合う！と仮定して考えた結果絶対につり合わなくなってしまいました。何がいけないかというと、仮定が間違っていたのです。よって使うおもりの個数は必ず偶数であると言えます。

（２）

３回目に８個使ってつり合うと仮定します。この８個（17g～43g）の和は270gなのでつり合うには片方の皿には135gのっています。片方の皿に奇数ｇのっているということは、おもりの個数も奇数個です。８個を奇数の和に分解すると、①１＋７もしくは②３＋５のどちらかになります。①のとき、１個の方には最大でも47gしかおけないので135gより小さくなります。②のとき、３個の方に最大で131g（41+43+47）しかおけないのでやはり135gより小さくなります。８個使ってつり合う！と仮定して考えた結果絶対につり合わなくなりました。やはりこれも仮定が間違っていたのです。よって３回目は８個ではないと分かります。

（3）３回目に使うのが１０個と提示してその具体例表記（4）４回目の具体例もあるのですがこれは手を動かしましょう。

いやこれ、難しすぎる。「説明しなさい」とか書いてあるけどもうやってること証明しなさいと同じだし、その方法がほぼ背理法だし…。（意図的にそう書いたので解説読みながら気が付いた人もいると思います。）背理法は結論が間違っていると仮定して進めた議論のうちに前提条件と矛盾するところが出てくることを述べて、仮定が間違っていた。つまり結論は正しい。という証明方法です。もっと驚くことはこの説明をほぼ完ぺきに受験会場でこなした6年生がこの世に存在することですね。代々武蔵は自校で過去問とその解答を作成、販売しているのですが、その解答の中には「受験生答案より」みたいなものが散見されて才能の差を感じます…。

　さて、このような数学での証明ですが、最初に触れるのは中学生の数学で三角形の合同を示すときかなと思います。３辺が等しい、２辺とその間の角が等しい、２角とその間の辺が等しい、の３つの条件のどれかを使って２つの三角形が合同であることを証明するのに苦戦している生徒をよく見ます。（＠両親の塾）この証明の話に入る前に、カリキュラム的にはひたすら「仮定」と「結論」を列挙する過程があります。なんの意味があんねんと思っていましたが案外大切だな、と最近思います。上にあげた問題では「３回目以降の操作で天びんがつり合っている」が「仮定」で、「おもりの数が偶数である」が「結論」です。（解説のところで使った背理法の仮定とは意味が違うので注意してください。）

　高校にも入ってもやはり数学で証明はあります。先ほど使った背理法による証明も高校生くらいでようやくまともに使い始めます。そして中学生のときの「仮定」と「結論」の部分もより詳しく、集合と論理という単元で扱います。

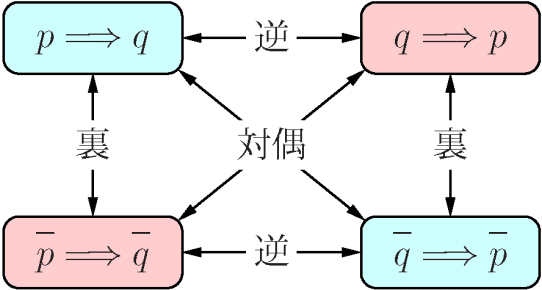
こんな図見たことありますかね。「⇒」の記号の左側が中学生での「仮定」、右側が「結論」になります。画像のｐとかｑとかその上に棒がついている（ｐに棒がついていたら「ｐではない」を表します）ところに「仮定」や「結論」の文章を入れて、「⇒」をならばと読んでいきます。この「仮定」と「結論」の組によって得られた新たな文章が正しいかどうかを考えていきます。

　「ｐならばｑ」が真であるとき、「ｐはｑの十分条件である」といい、「ｑはｐの必要条件である」といいます。また、「ｐならばｑ」が真で「ｑならばｐ」が真であるとき「ｐとｑは同値である」や「ｐはｑの（ｑはｐの）必要十分条件である」といい、ｐとｑが全く同じことを指していることを述べています。一方「ｐならばｑ」が真で「ｑならばｐ」が偽であるとき、「ｐはｑの十分条件であるが必要条件でない」、「ｑはｐの必要条件であるが十分条件でない」といいます。こんな風に中学生で考えていた「仮定」と「結論」を入れ替えたときどうなるかまで考えていくようになります。（中学生のうちは十分性だけを考えていた、ということも出来ます。）

　そしてここでもう一つ大切なのは、先の画像の「対偶」で結ばれた青枠同士赤枠同士の真偽が一致するということです。「ｐならばｑ」と「ｑでないならばｐでない」の真偽は一致します。詳しい説明はどこかで学んでください…。

　ここでまた中学入試から１問。理科ですがもはや数学です。

　この問題見た時感動しました。いやほんとに。先ほどの画像のｐとかｑに当てはまる文章を考えてみます。

ｐ：ある固体を塩酸にいれて水素が生じる

ｑ：ある固体は亜鉛である

とすると、(ア)は「ｐならばｑ」、(イ)は「ｐでないならばｑでない」、(ウ)は「ｑならばｐ」、(エ)は「ｑでないならばｐでない」、の4つになっています。対偶の関係になっているのは(ア)と(エ)、(イ)と(ウ)です。つまり答えはどう頑張ってもこのペア以外にありません。多少知識があれば(ウ)が正しいことが分かります。なので答えは(イ)と(ウ)になります。もちろん小学生がこんなこと知っているわけありませんし、知らなくてもよく読めば解けます。

　中学入試の問題の中にもこのようにその先の数学の世界へとつながる入り口となっているような問題があります。そしてこの論理の世界は文系だから数学やらないし…とはできない世界です。法律の条文を読もうとしたとき何が仮定になっているか、それをきちんと満たしているかは重要ですし、「論理学」の専攻は多く文学部にあったりします。経済学部が文系なのは日本くらいのもので、かなり詳しく数学をやる場合が多いです。（僕も未だに数学やってます…。）日常生活で安易に対偶を考えると適当なインチキ発言に出くわすのでそうしたことから身を守る意味でも大切です。

　この先どのような道であれついてまわる論理の話だからこそ、そしてきちんと考えれば小学生でも解けるからこそ、ちょっと早い段階で問うてみているのだと思います。とりあげた2題こそまさしく「論理的思考」を求められた問題と言えるかもしれません。