ねこっちです。本記事では、$${n=2,3}$$の場合におけるサイン様多項式を1つずつ与えてみます。なお、「サイン様多項式」の定義については、以下の記事をご覧ください。

　それでは、始めます。

nが2の場合の具体例

　まずは$${n=2}$$の場合におけるサイン様多項式$${T_2(x)}$$を与えます。無数にある多項式から条件を満たすものを探すのは極めて難しいので、次のような方針をとります。

①まず「極大値と極小値がそれぞれすべて等しい多項式」のうち、$${x=0,\pm x_2}$$で極大値$${M}$$を、$${x=\pm x_1}$$で極小値$${m}$$をとるもの$${f(x)}$$を探す。ここで$${x_2>x_1>0}$$とする。

②①の多項式の$${x}$$に、「$${t=0}$$のとき0、$${t=1}$$のとき$${x_1}$$を、$${t=2}$$のとき$${x_2}$$の値をとる、単調増加の奇関数多項式$${g(t)}$$」を代入する。

③最後に次式を計算することで、求める多項式を得る：

$$
T_2(x)=\frac{2}{M-m}f(g(x))-\frac{M+m}{M-m}
$$

手順①

　ここでは偶関数に目星をつけて探してみます。まず、0以外の$${x}$$で極小値が0となる、原点を通る3次関数を考えます。たとえば、次のようなものが見つかります。

$$
f_1(x)=x^3-2x^2+x\quad\dots(1)
$$

　これは$${x=1/3}$$で極大値$${4/27}$$を、$${x=1}$$で極小値$${0}$$をとります。$${x=0}$$での値と、極小値がともに0なので、この関数(1)に$${x^2}$$を代入すれば、極大値と極小値がそれぞれすべて等しいような、条件を満たす偶関数が得られます：

$$
f(x)=f_1(x^2)=x^6-2x^4+x^2
$$

　なお、関数$${f(x)}$$は$${x=\pm 1/ \sqrt{3}}$$で極大値$${4/27}$$を、$${x=0,\pm1}$$で極小値0をとる関数になっています。

手順②

　次に、点$${(0,0),(1,1/ \sqrt{3}),(2,1)}$$を補間する単調増加の奇関数多項式を求めます。実は、このような条件を満たす奇関数多項式は5次関数以上でなければならないのですが、ここではその証明は省きます。このような5次関数を$${g_1(x)=c_1x+c_2x^3+c_3x^5}$$とおき、条件を代入すると

$$
\left\{  \begin{array}{c} c_1+c_2+c_3=1/\sqrt{3} \\ 2c_1+8c_2+32c_3=1 \end{array} \right.
$$

　となります。この連立方程式の拡大係数行列

$$
\left( \begin{array}{cccc} 1 & 1 & 1 & 1/\sqrt{3}\\ 2 & 8 & 32 & 1 \end{array} \right)
$$

を簡約階段行列にすると、

$$
\left(\begin{array}{cccc}1&0&-4&\frac{4}{3\sqrt{3}}-\frac{1}{6}\\0&1&5&\frac{1}{6}-\frac{1}{3\sqrt{3}}\end{array}\right)
$$

となるので、この連立方程式の解は$${\alpha}$$を任意定数として

$$
\left\{\begin{array}{c}c_1=4\alpha+\frac{4}{3\sqrt{3}}-\frac{1}{6}\\c_2=-5\alpha-\frac{1}{3\sqrt{3}}+\frac{1}{6}\end{array}\right.
$$

となります。元の関数$${g_1(x)}$$が単調増加となるような$${\alpha}$$を１つ選ぶと、例えば$${\alpha=1/1000}$$がそれに適するので、これを代入して

$$
g_1(x)=\left(\frac{4}{3\sqrt{3}}-\frac{61}{375}\right)x+\left(-\frac{1}{3\sqrt{3}}+\frac{97}{600}\right)x^3+\frac{1}{1000}x^5
$$

を得ます。

手順③

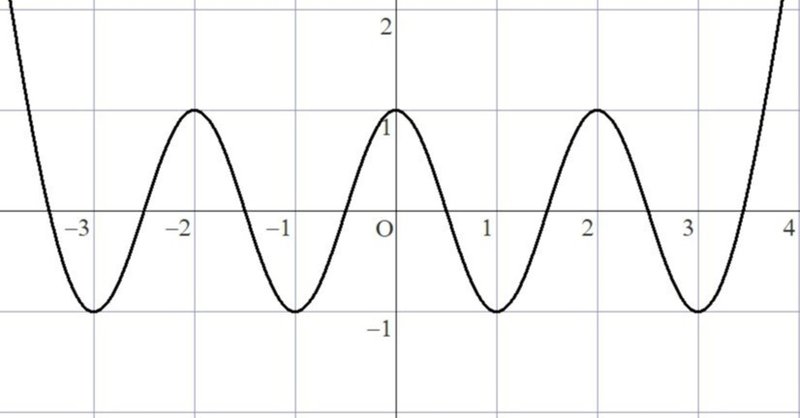
　以上より、求める多項式は$${6\times5=30}$$次関数となり、次式になります。

$$
T_2(x)=-\frac{27}{2} f(g(x))+1
$$

　グラフは次の通りです。

nが3の場合の具体例

　nが2の場合と同様に、3階サイン様多項式の1つを求めてみましょう。

手順①

　まず、適当に4次関数を書き出します。

$$
f_2(x)=x^4-4x^2
$$

この4次関数は、$${x=0}$$で極大値0をとり、$${x=\pm\sqrt{2}}$$で極小値$${-4}$$をとります。次に、極大値を与える$${x}$$以外の点でこの関数が原点を通るように、関数を平行移動します。方程式$${f_2(x)=0}$$の0以外の解は$${x=\pm2}$$なので、次のようになります。

$$
f_3(x)=f_2(x-2)
$$

$${f_3(x)}$$は$${x=2\pm\sqrt{2}}$$で極小値$${-4}$$を、$${x=2}$$で極大値0をとります。

したがって、以下の関数

$$
f_4(x)=f_3(x^2)=f_2(x^2-2)\\=x^8-8x^6+20x^4-16x^2
$$

は極大値と極小値がそれぞれすべて等しい関数であり、極小値$${-4}$$を与える$${x}$$は$${x=\pm\sqrt{2-\pm\sqrt{2}}}$$（複号任意）、極大値0を与える$${x}$$は$${x=0,\pm\sqrt{2}}$$となります。

手順②

　次に、点$${(0,0),(1,\sqrt{2-\sqrt{2}}),(2,\sqrt{2}),(3,\sqrt{2+\sqrt{2}})}$$を補間する単調増加の奇関数多項式を求めます。これは7次関数で探すのが適切であると考えました。そこで、このような多項式を

$$
g_2(x)=C_1x+C_2x^3+C_3x^5+C_4x^7
$$

とおいてみます。条件より、連立方程式

$$
\left\{\begin{array}{c}C_1+C_2+C_3+C_4=\sqrt{2-\sqrt{2}}\\2C_1+8C_2+32C_3+128C_4=\sqrt{2}\\3C_1+27C_2+243C_3+2187C_4=\sqrt{2+\sqrt{2}}\end{array}\right.
$$

が成り立ちます。この方程式の拡大係数行列

$$
\left(\begin{array}{ccccc} 1&1&1&1&\sqrt{2-\sqrt{2}}\\ 2&8&32&128&\sqrt{2}\\ 3&27&243&2187&\sqrt{2+\sqrt{2}}\end{array}\right)
$$

を簡約階段行列にすると、次のようになります。

$$
\left(\begin{array}{ccccc} 1&0&0&36&\frac{3}{2}a-\frac{3}{10}b+\frac{1}{30}c\\ 0&1&0&-49&-\frac{13}{24}a+\frac{1}{3}b-\frac{1}{24}c\\ 0&0&1&14&\frac{1}{24}a-\frac{1}{30}b+\frac{1}{120}c\end{array}\right)
$$

ここで$${a=\sqrt{2-\sqrt{2}},b=\sqrt{2},c=\sqrt{2+\sqrt{2}}}$$とおきました。したがって、連立方程式の解は$${\beta}$$を任意定数として

$$
\left\{\begin{array}{c}C_1=-36\beta+\frac{3a}{2}-\frac{3b}{10}+\frac{c}{30}\\ C_2=49\beta-\frac{13a}{24}+\frac{b}{3}-\frac{c}{24}\\ C_3=-14\beta+\frac{a}{24}-\frac{b}{30}+\frac{c}{120}\end{array}\right.
$$

となります。$${\beta=10^{-5}}$$とすると$${g_2(x)}$$は単調増加となるので、求める7次関数は次のようになります。

$$
g_2(x)=\left(-36\beta+\frac{3a}{2}-\frac{3b}{10}+\frac{c}{30}\right)x+\left(49\beta-\frac{13a}{24}+\frac{b}{3}-\frac{c}{24}\right)x^3\\+\left(-14\beta+\frac{a}{24}-\frac{b}{30}+\frac{c}{120}\right)x^5+\beta x^7,\quad \beta=10^{-5}
$$

手順③

　以上から、求める3階サイン様多項式の１つとして次を得ます。

$$
T_3(x)=\frac{1}{2}f_4(g_2(x))+1
$$

　グラフは以下の通りです。

最後に

　今回、$${\alpha}$$や$${\beta}$$の値の選定にはグラフ描画ソフトを用いましたが、この値はできるだけ小さくとった方が多項式がサインカーブに近づきました。この現象の解明は今後の課題とします。

　また、今回用いた方法はより高階のサイン様多項式の計算にも使えるのではないかと思いましたが、その点についての考察も今後の課題とします。

　ただの遊びで思いついたサイン様多項式でしたが、計算している時間はなかなか面白いものでした。ただ、現段階ではこの「サイン様多項式」は何に応用できるかわからないので、この点についても今後探究できればと思います。

　以上、ねこっちでした。最後までお読みくださりありがとうございました。