尤度比検定とは

尤度比検定とは帰無仮説とそうでない一般の場合（対立仮説）
の尤度の比$${L}$$を計算し

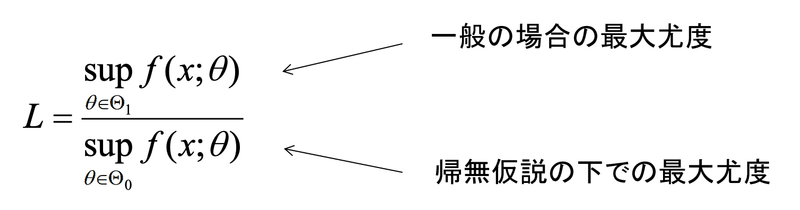
この尤度比$${L}$$を
対数の2倍の値を計算し$${\chi^2}$$検定統計量に従う形にして検定する

$$
\chi^2 　〜　 2log(L)　where   n \rightarrow \infty
$$

なお検定統計量が
$${\chi^2}$$分布に従うことはWilksの定理で保証されているが
発展的な内容なので参考文献を載せるのみにとどめておく

尤度比検定の例題

検定統計量の計算例

$${X_1, X_2, X_3, \cdots, X_n}$$の確率変数で
パラメーターが$${n, \theta_1, \theta_2, \cdots, \theta_n}$$

$$
\sum_i X_i = n \\{}\\
\sum_i \theta_i = 1
$$

の多項分布を考える

帰無仮説を

$$
\theta_1 = \theta'_1, \theta_2 = \theta'_2,\theta_3 = \theta'_3 \cdots \theta_n = \theta'_n
$$

としたときの尤度比の検定統計量を考える

尤度比検定の検定統計量の計算は

1. 尤度関数計算

2. 帰無仮説と対立仮説の尤度関数計算

3. 尤度比計算

4. 検定統計量計算

の順番で考える

検定統計量を用いた尤度比検定

上記の多項分布の検定統計量を用いて尤度比検定を行う

以下は曜日ごとの某会社への問い合わせ回数だとする

帰無仮説のもとではすべての曜日においてパラメーターが等しいので
$${\sum_i \theta_i = 1}$$より$${\theta_1 = \theta_2 = \cdots = \theta_n = \frac{1}{7}}$$

$$
\begin{aligned}
2log(\frac{L_1}{L_0}) &= 2 \sum_i x_i log(\frac{x_i}{n \theta_i})\\{}\\
&= 2\bigg(7log\big(\frac{7}{49 \times \frac{1}{7}}\big) \times 3log\big(\frac{3}{49 \times \frac{1}{7}}\big) \times \cdots \times 13log\big(\frac{13}{49 \times \frac{1}{7}}\big)  \bigg)\\{}\\
&= 15.57
\end{aligned}
$$

自由度6の$${\chi^2}$$統計量の上側5％は12.59（＜ 15.57）であるので
帰無仮説は棄却され対立仮説「曜日によって回数の差がある」と言える

適合度検定との比較

$${\chi^2}$$統計量を用いる検定に適合度検定がある

$$
\begin{aligned}
& \sum_i\frac{(観測度数_i - 期待度数_i)^2}{期待度数_i} \\{}\\
&= \sum_i \frac{(O_i - E_i)^2}{E_i}
\end{aligned}
$$

先ほどの例題を適合度検定の検定統計量を用いて求めてみる
$${E_i = \frac{49}{7} = 7}$$より

$$
\begin{aligned}
& \sum_i \frac{(O_i - E_i)^2}{E_i}\\{}\\
&=  \frac{(7 - 7)^2}{7} + \frac{(3 - 7)^2}{7} + \cdots + \frac{(13 - 7)^2}{7}\\{}\\
&= 15.14
\end{aligned}
$$

と同様に帰無仮説が棄却できる

つまり、適合度検定と尤度比検定は漸近的に（nを大きくすれば）
同じことを言っている