変数変換とは

変数変換は、統計分析やデータ処理において、変数の値や性質を変更する手法
これによって、データの分析やモデルの構築が容易になったり、データの分布や関係性を改善したりすることが可能になる

変数変換にはいくつかの種類があるが今回は、1変数2変数の変数変換を紹介した後その他の変換について触れていく

1変数の変数変換による確率関数の変化

変数変換によって確率関数の$${dx}$$と積分区間が変化する

例 :

標準正規分布を
確率変数を$${X^2 \rightarrow Y}$$に変換したとする

$${dx}$$と$${dy}$$の関係式は

積分区間について
$${x}$$が0以上以下で2分割し
第1項と第2項が等しいことを利用すると

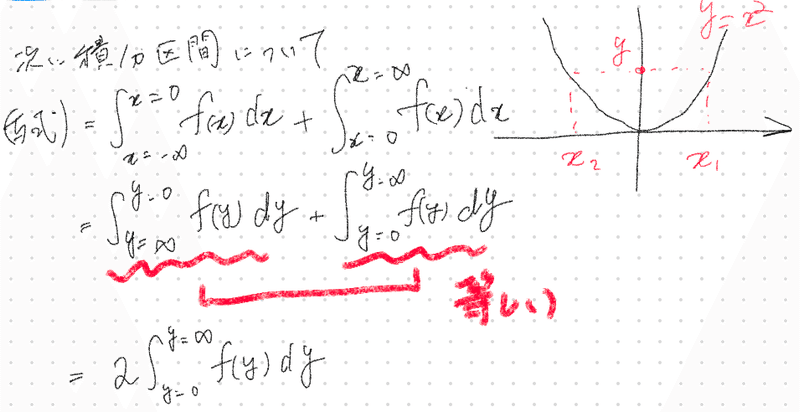
最終的に確率関数は以下の通りとなる

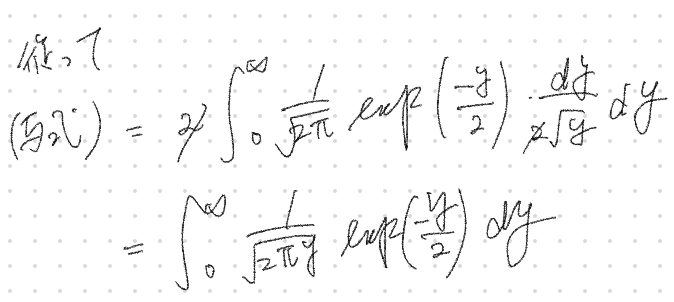
また他の問題も下記取り上げる

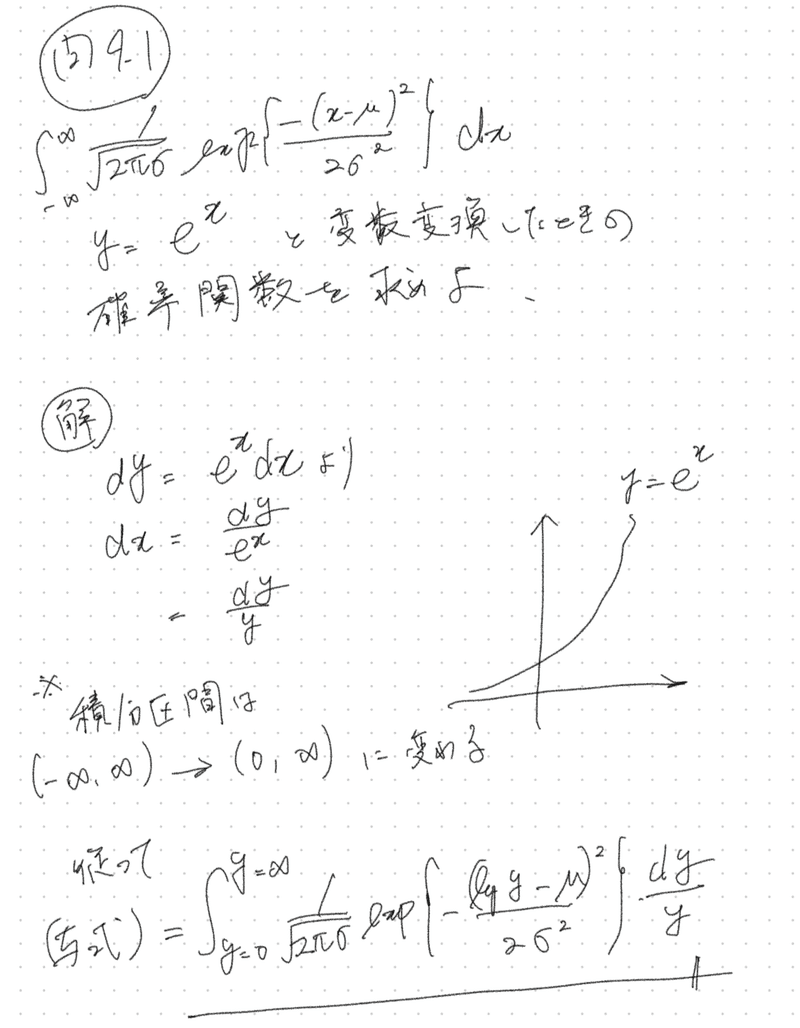
2変数の変数変換による確率関数の変化

2変数の変数変換も同様に確率関数の$${dx}$$と積分区間が変化する
1変数の場合は下記のように$${dx}$$が変化するが

$$
f_y(y) = f_x(x)\frac{\partial x}{\partial y}\\
{}\\
→ f_y(y)dy = f_x(x)dx
$$

2変数の場合は下記のように
確率関数の$${dx}$$を計算するときに
ヤコビアン$${|J|}$$を計算する必要がある

$$
f_x(x)f_y(y) = f_z(z) f_w(w) |J|\\
$$

において

$$
\begin{vmatrix}
 \frac{\partial Z}{\partial X} &   \frac{\partial Z}{\partial Y} \\{}\\
 \frac{\partial W}{\partial X} &   \frac{\partial W}{\partial Y}
\end{vmatrix}
= |J|
$$

ヤコビアンとは

2変数変換におけるヤコビアンとは
微小面積の変換前と変換後の面積比（Scale factor）である

例として半径3の円を極座標変換した場合を考えよう

極座標変換とは
円の$${x,y}$$を半径と角度の$${r, \theta}$$に変換することである

$${r}$$の範囲は円半径の範囲なので0から3
$${\theta}$$の半径は円が取りうる角度の範囲なので0から2 $${\pi}$$

これを図に表すと下図のようになる

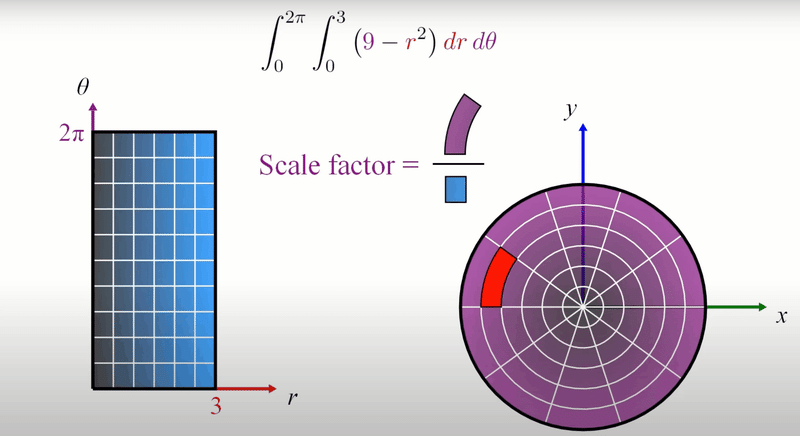
ここで微小面積を白線で表すと変換した前と後で
面積の値が変わっていることに気がつくだろうか

例えば左の長方形の微小面積は一定だが、
右の円の微小面積は中心部が小さく、外側が大きい

この微小面積の変換前と変換後の面積比（Scale factor）を表したのが
ヤコビアンである！

ヤコビアンを使えば上の例$${r,\theta → x,y}$$だと

$$
dxdy = |J| drd\theta
$$

とい微小区間の面積の等式ができる

このときのヤコビアンは下記で求めることができる

$$
\begin{vmatrix}
 \frac{\partial x}{\partial r} &   \frac{\partial x}{\partial \theta} \\{}\\
 \frac{\partial y}{\partial r} &   \frac{\partial y}{\partial \theta}
\end{vmatrix}
$$

線型結合の2変数の変数変換における確率関数の変化

$${X,Y → Z,W  where  Z = aX + bY,  W = Y}$$ の変換は
同時確率分布とヤコビアンを用いて

$$
f_x(x)f_y(y) = f_z(z) f_w(w) |J|\\
$$

ただし

$$
\begin{vmatrix}
 \frac{\partial Z}{\partial X} &   \frac{\partial Z}{\partial Y} \\{}\\
 \frac{\partial W}{\partial X} &   \frac{\partial W}{\partial Y}
\end{vmatrix}
= a    (= |J|)
$$

となったのだった

これを両辺$${w}$$について積分すると$${\int_{-\infty}^{\infty} f_w(w)dw  = 1}$$に注意して

$$
\int_{-\infty}^{\infty} f_x(x)f_y(y) \frac{1}{|J|}dw = f_z(z)
$$

$${(x,y) = (\frac{z}{a} - \frac{bw}{a},w)}$$を代入すると

$$
f_z(z) = \int_{-\infty}^{\infty} \frac{1}{|a|} f_x(\frac{z}{a} - \frac{bw}{a}) f_y(w)dw
$$

となる

これを用いて下記の問題を解いていこう
$${X,Y → Z,W  where  Z = aX + bY,  W = Y}$$の
$${a = b = 1}$$の場合に該当することに注意

その他の変換

対数変換

対数変換$${y = logx}$$は非負値$${x}$$を正負無限大$${y}$$に変換するときに用いる

費用や価格、人口などの指数的に増加するデータの膨張を抑えるときに用いることが多く$${y = logx}$$の$${x}$$に代入する

べき乗変換

べき乗変換$${y = x^a}$$は正負無限大$${x}$$を非負値$${y}$$に変換するときに用いる

対数変換とは逆に変化の少ないデータに対して膨張させたいときに用いる

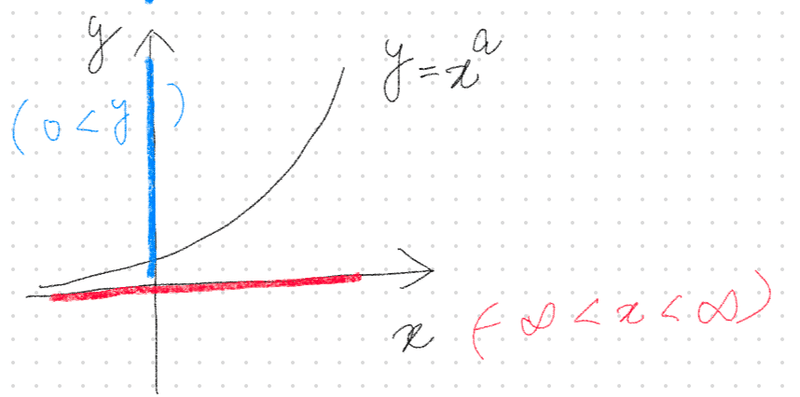
ロジット変換

ロジット変換$${y = log \frac{x}{1-x}}$$は確率のような0から1をとる$${x}$$を正負無限大$${y}$$に変換するときに用いる

これの逆関数がロジスティック変換である

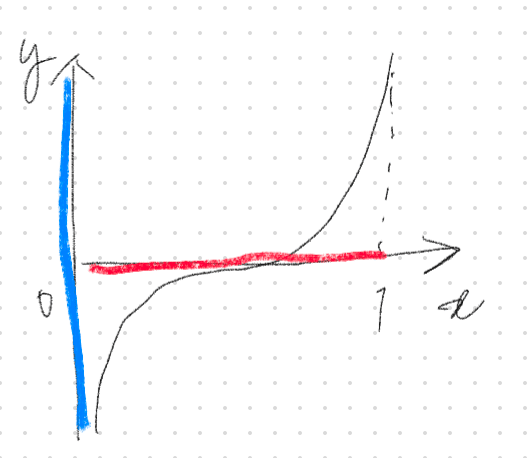
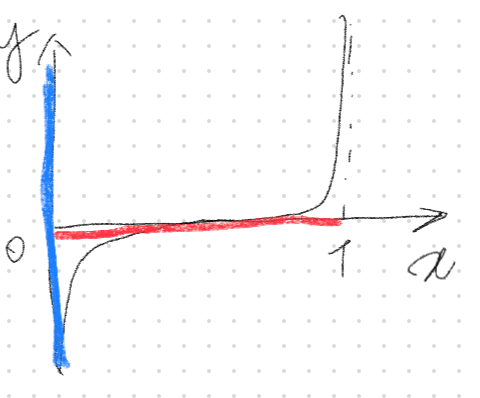
プロビット変換

プロビット変換$${y = log \frac{x}{1-x}}$$は確率のような0から1をとる$${x}$$を正負無限大$${y}$$に変換するときに用いる

ロジット変換と同じようなことをしているが
プロビット変換の方が裾野の部分が狭いので
確率が0or1のように極端な値を取ることが少ないときに有用である

詳しくは下記
http://data-science.tokyo/ed/edj1-5-3-1-1.html