AHC022 解説
RECRUIT 日本橋ハーフマラソン 2023夏(AtCoder Heuristic Contest 022) のコンテスト中 & 後に考えたこと、あと提出での改善内容について書いています。
最終的には暫定テスト53位、システムテスト1,619,576,273,166点で47位相当の解法になります。
問題へのリンク
方針立て
ワームホール - 出口セルの対応関係をうまく推定する問題です。
配置と計測の2段階に処理が分かれていますが、配置について考えることは
計測でワームホール - 出口セルの対応関係をうまいこと推測させられるような配置にする
配置時コストがなるべく小さくなるような配置にする
ことなので、先に計測の段階でどうやってワームホール - 出口セルの対応関係を推定していくかについて考えます。
推定ですが、計測結果として渡される値$${m}$$が$${0}$$もしくは$${1000}$$の時に気をつけた上で、単純にベイズ推定すれば良さそうです。
ここの計測で行う処理については実質ベイズ推定の話になるので、別項目にて解説します。
そんなわけで配置について考えますが、まずは特徴の把握から。自分が決めるグリッドのセル$${(i, j)}$$の値$${P_{i,j}}$$について、
隣接させるセル同士の値の差が大きいほどコストが大きくなる
$${\max{(P_{i, j})}}$$と$${\min{(P_{i,j})}}$$の差は大きいほど推定が捗りやすそう
その代わり配置時コストが上がっていく
$${P_{i,j}}$$の値が1種類しかかない場合は、当然何も推定できない
と、ざっくりとこんな感じで、大きい値と小さい値を置く際にパッと思いついたのが
グラデーションぽくしておく
そのまま差の大きい2値を隣接させておく
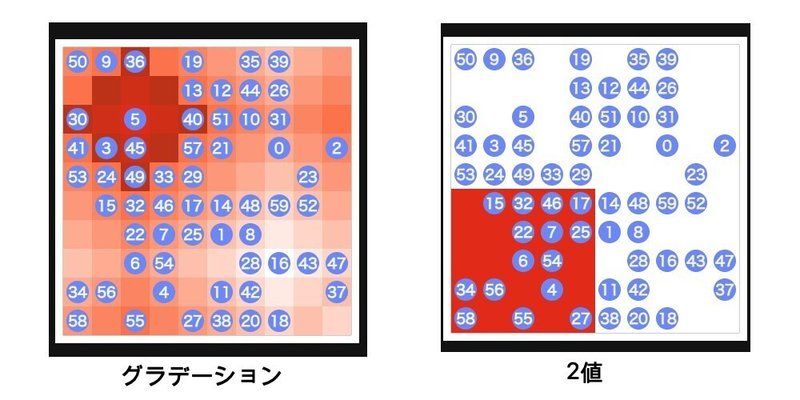
それぞれ
グラデーションのパターンだと配置コストが抑えられるが、隣接しているセル同志の値の差が小さい
2値だと配置コストがとにかく高い
という問題がありますが、グラデーションのパターンだと、計測時にどのように移動させたとしても、隣接しているセル同志の値の差が小さいため、
そのまま隣接している出口セルを識別するのが難しそうです。
そのため、差の大きい2値を隣接させるパターンを選択しています。
(余談ですが、コンテスト終了後の上位勢の多くの解法がグラデーションのように極端に差のある2値を隣接させない配置になっています。)
2値をどのように配置するかですが、上図の2値にすればいいと考えました。
同じ行や同じ列に位置する出口セルのペアが存在するのは($${L \lt N}$$より)確実なので、全ての行/全ての列に対して
一行まるまる/一列まるまる どちらかの値にすると計測時に2値に分けられない($${=}$$ 全ての行を一行まるまる特定の値にすると、同じ行に位置する出口セルのペアが計測で分別できない)たとえば1つの値に対して別の値をいろいろな箇所に飛び飛びで入れると、配置時コストがエグくなってしまう $${\leftarrow}$$ 飛び飛びではなく塊を入れたい
たとえば1つの値に対して別の値を1セル分だけ入れた場合、配置時コストは抑えられるが、1セル分だけしかないため、計測に手数がかかりそう
という判断から、先の図のような「2値に分ける場合、1つの値を$${\displaystyle \frac{L}{2} \times \frac{L}{2}}$$の領域にセットして、それ以外の領域は別の値にする」ということにしました(片方の面積が$${\displaystyle \frac{L^2}{4}}$$にしよう、という具体的な数値についてはただの勘です)。
まあ配置時コストや計測時コストを減らす際に配置は変わっていくのですが、基本的な方針は「どの出口セルのペアにおいても、移動後の位置が差の大きい2値に別れるような移動が存在するような配置にする」というのを念頭に置いて、いかにコストを減らすか、ということに試行錯誤していました。最終的な配置については後述してあります。
最後に2値はどう決めるか、ということですが、2値は差がわかっていればよいだけです。
これはもう$${S, N, L}$$に依存するのは明らかだったので、$${S, N, L}$$の値を決めて実験して値を直接コードに埋め込むことにしました。
計測で行う処理について
主にベイズ推定の話になります。ご存知の方は飛ばしてください。
まずベイズの定理について、定理の導出の詳細は書籍等をおって欲しいですが、ざっくり書くと、確率変数$${x, y}$$に従う確率分布$${P(x, y)}$$対して、
事象$${x=x_i, y=y_j}$$が同時に発生する確率を$${P(x=x_i, y=y_j)}$$と表す
事象$${x=x_i}$$が発生した場合に事象$${y=y_j}$$が発生する条件付き確率を$${P(y=y_j | x=x_i)}$$と表す
$${y}$$の値によらず事象$${x=x_i}$$が発生した場合の確率を$${P(x=x_i)}$$と表す(周辺化)
$${x}$$の値によらず事象$${y=y_j}$$が発生した場合の確率を$${P(y=y_j)}$$と表す(周辺化)
と、$${P(x=x_i, y=y_j) = P(x=x_i)P(y=y_i | x=x_i) = P(y_j)P(x=x_i | y=y_j)}$$となります。
特に右側の等式を整理した$${\displaystyle P(y=y_j | x=x_i) = \frac{P(y=y_j)P(x=x_i | y=y_j)}{P(x=x_i)}}$$の部分をベイズの定理と呼びます。
右辺分母の$${P(x=x_i)}$$は正規化定数とも呼ばれます。
$${P(y=y_j)}$$を事前確率、$${P(y=y_j | x=x_i)}$$を事後確率といいます。
今回のケースだと条件付き確率$${P(x=x_i | y=y_j)}$$は「出口セルが$${y_j}$$の時に計測からデータ$${x_i}$$が得られる確率」を表していて、データを変数としてモデルの尤もらしさを表しているので、$${P(x | y=y_j)}$$は尤度関数とよばれます(単に尤度とも)
これを今回の話に置き直します。
流れを書くと、やりたいこととしては、ワームホールAがどの出口セルにつながっているかを知りたいので、
ワームホールAが出口セル$${i}$$につながっている確率を、確率変数$${y}$$を用いて$${P(y=i), i \in {0, 1, \dots, N-1}}$$とします。
どこかの出口セルにつながっているのは確実なので$${\displaystyle \sum_{i=0}^{N-1}{P(y=i)} = 1}$$です。
初期状態だと何の探索もしていないので、どの出口セルにつながっているかの可能性は同じ $${\displaystyle \rightarrow P(y=i) = \frac{1}{N}}$$です。これが初期状態の事前確率になります。計測します。ワームホール$${A}$$から$${(r, c)}$$だけ移動しますよ、という情報をA r cという形で標準出力すると$${m}$$という値が返ってきました。
ここで各出口セル$${i}$$に対して「ワームホールAの出口セルが$${i}$$の場合に、その出口セルの位置から$${(r, c)}$$だけ移動した時の$${P}$$の値$${P_i}$$を計測したら$${m}$$という値が得られる確率」が尤度の値$${P(x=(r, c, m) | y=i)}$$にあたります。
$${m}$$の値と$${P_i}$$の値が分かれば$${F}$$が($${m = 0, 1000}$$の場合を除いて)確定できるので、正規分布から尤度の値を計算できます。$${m=0,1000}$$の場合でも累積分布関数から尤度の値は計算できます。具体例は後述。1, 2から各出口セルに対して尤度の値と事前確率がわかっているので、事後確率を求めに行きます。
ベイズの定理を改めて見返すと正規化定数はいくらなのか分かりませんが、計測をしたところでワームホールAはどこかの出口セルにつながっていることは確定なので、$${\displaystyle \sum_{i=0}^{N-1}{P(y=i | x=(r, c, m))} = 1}$$です。
なので各出口セル$${i}$$に対応する$${P(y=i)P(x=(r, c, m) | y=i)}$$の和をとってそれで割ってやれば事後確率になります。
ベイズの定理ですが、正規化定数の項を消して$${P(y=y_j | x=x_i) \propto P(y=y_j)P(x=x_i | y=y_j)}$$と表現されることもあります。
流れはかけたので具体例に移ります。$${L=5, N=5, S=4}$$で、$${P}$$の値と出口セルの位置を以下のように設定したとします。

それではワームホール$${0}$$から決めていきたいと思います。初期状態だとどの出口セルにつながっているかわからない&どこかの出口セルにはつながっているので、ワームホール0の出口セルの確率分布は一様分布で各確率は$${1 / N = 0.2}$$になります。
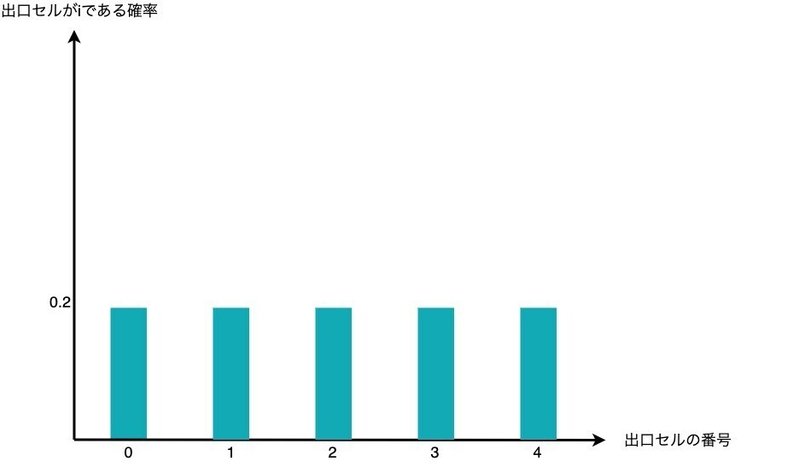
計測として、ワームホール0についてどこかの出口セルにでた後、下に1, 右に2動かしてみることにします。なので0 1 2と標準出力したところ、$${m = 2}$$という値が返ってきました。
仮にワームホール0が出口セル0につながっている場合、下に1, 右に2移動した$${P}$$の値は8です。$${m}$$として得られたのは2なので、$${F}$$の値は$${-6}$$です。
厳密には$${m}$$は$${\max{(0,\min{(1000, round(2 + f(S)))})}}$$なので、$${F}$$の値は$${-6.5 \sim -5.5}$$の$${f(S)}$$から計算されたものです。
そして$${f(S)}$$は平均0、標準偏差$${S}$$の正規分布からサンプリングしたとのことなので、その正規分布で$${-6.5 \sim -5.5}$$となる確率を求めればいいです。下図のライム色の部分の面積を求めることになります。
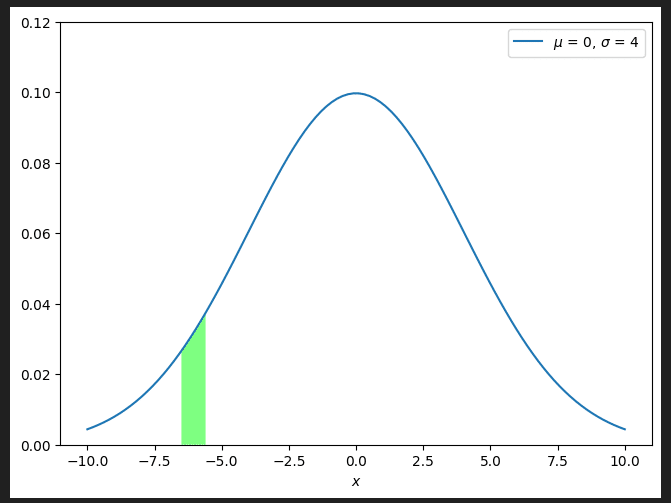
面積を求める方法は実際にどうするのがベターかは分かりませんが、自分は面積を求める箇所について$${20000}$$分割し、その平均を求めたものを事前計算しておきました。要は粗い区分求積法みたいな感じです。
$${\displaystyle g(x, S, \mu) = \frac{1}{\sqrt{2\pi S^2}}e^{-\frac{(x-\mu)^2}{2S^2}}}$$として、具体例の場合だと
(面積部分) $${\displaystyle = \int_{-6.5}^{-5.5}{g(x, 4, 0)dx} \approx \frac{\displaystyle \sum_{i=0}^{20000}{g(\displaystyle -6.5+\frac{i}{20000}, 4, 0)}}{20001}}$$
と近似した値を求めました。
そんなわけでこれを計算した結果が大体0.032484くらいです。これで出口セル$${0}$$について尤度の値が求まりました。他の出口セルも同様に計算します。
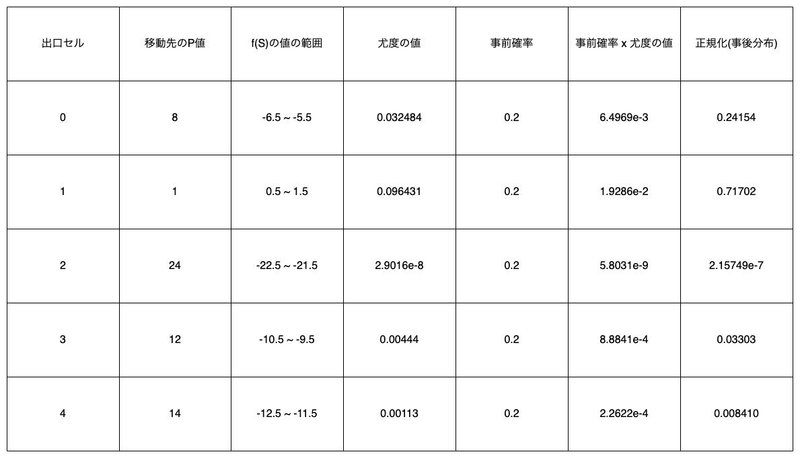
計算しました。これに対して全ての(事前確率)$${\times}$$(尤度の値)の和を取ると約$${0.0268978}$$で、それで各出口セルの(事前確率)$${\times}$$(尤度の値)を割れば正規化され事後分布になります。というわけで事後分布を求めることができました。
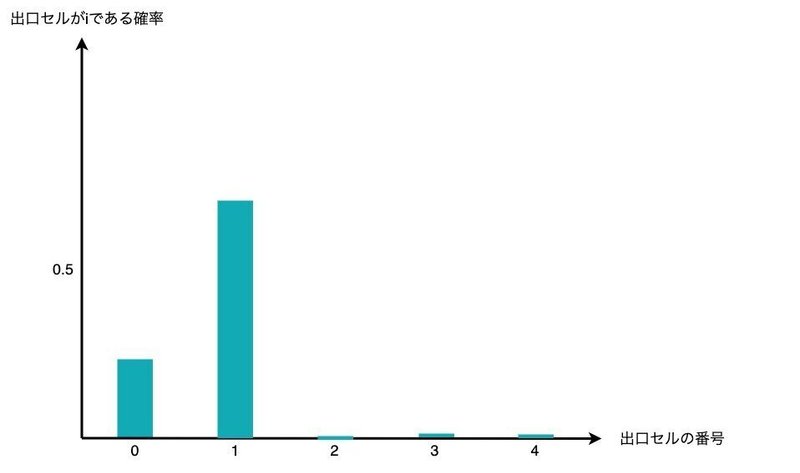
画像の比率は正しくできていないですが勘弁してください。
事後分布はそのまま次の計測の事前分布として使えるので、これを繰り返すことでつながっていると思われる出口セルの確率が上がり、閾値を決めてそれを超えたところで「ワームホールAの出口セルが〇〇に決まった」として、別のワームホールについて計測をすればいいです。
閾値は各々で決めたらいいですが、決める指標としては、$${(閾値)^N}$$の値が「全部のワームホール - 出口セルの対応関係が正解する確率」になるので、それを考えればいいと思います。
私の場合は$${N=100}$$の時でも90%程度完全正解して欲しいので閾値を0.999に決めました$${\dots}$$と言いたいところなのですが、0.998に設定していたつもりだったところ、コンテスト終了15分前に閾値を0.999に設定していることに気づき、それを基準にして色々なパラメータを決めてしまっていたため、0.999のまま修正しませんでした。
これで基本的な推定部分は終わりで、あとは$${m=0, 1000}$$の場合です。
具体例のところで$${m=0}$$だった場合、出口セル$${0}$$の「$${f(S)}$$の値の範囲」はどうなったでしょうか。
$${m}$$は$${\max{(0,\min{(1000, round(2 + f(S)))})}}$$なので、$${f(S)}$$は$${-7.5}$$以下であればどんな値でも$${m=0}$$となります。というわけで尤度の値として下図のライム色の面積を求めなければいけないわけです。
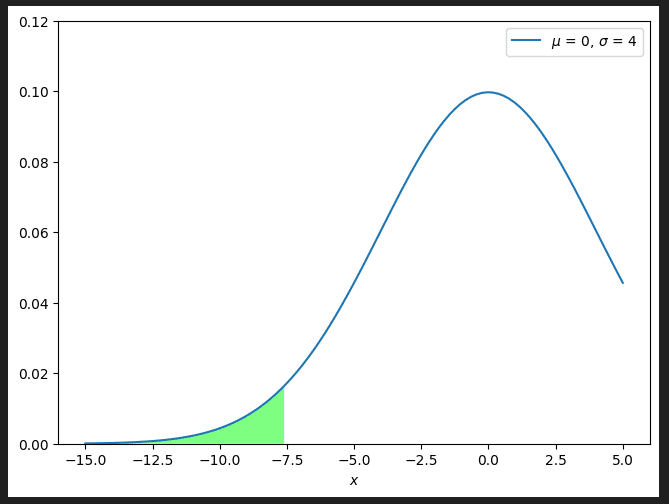
これに関しては正規分布の累積分布関数を求めればいいです。計算の仕方はわからないですが、SciPy.stats.cdfを使って事前に値を埋め込んでおけばいいです。
具体的には、$${m}$$が0未満にはならないので$${m = 0, P = 1000}$$の時$${f(S)}$$は$${-999.5}$$以下で、$${-999.5}$$の時の累積分布関数の値さえ事前に埋め込んでおけばよいです。この値を$${CDF_{-999.5}(S)}$$とします。それさえあれば、例えば$${m=0, P=999}$$の時は$${f(S)}$$は$${-998.5}$$以下で、前述の通常時の面積の求め方を利用して$${CDF_{-999.5}(S) + \int_{-999.5}^{-998.5}{g(x, S, 0)dx}}$$とすれば良いですね。都度計算だと時間がかかるので事前計算しておきましょう。
$${m=1000}$$の場合は逆に$${f(S)}$$が〇〇以上の時であればどんな値でも$${m=1000}$$となります。正規分布は全領域で積分すると1になるので、$${m=0}$$の時と同じようにcdfを使って「1 - ($${f(S)}$$が〇〇以下の時の面積)」で求まります。
残るのは「より早く閾値を越えさせるためにどのように移動させるか」という部分です。これは事前確率が高い2つの出口セルをピックアップして、それらが$${P}$$の値の最低値と最高値のところに行くような移動をさせることにしました。あの2値のグラフはそれが実現できるようにしています。
改善フェーズ
方針立てたものを実装したところで、やはりより良い解法が浮かぶものです。その中で主に効果があったものを、なぜそれに思い至ったかをできる限り明確にしながら書けたら、と思います。
■計測処理で、すでに確定した出口セルについては、他のワームホール - 出口セルの計測の時にその出口セルの確率を0にする
こうすればワームホール - 出口セルの対応関係を決めるたびに、区別する出口セルの数も減るので計測の時間が短くなります。
「なぜそれに思い至ったかをできる限り明確にしながら書けたら、と思います」と書いておきながら、「計測時コストを減らしたいのならこれは自然な発想」としか説明できません。
■計測処理で、ピックアップする事前確率が高い出口セルのペアの候補が複数ある場合に、移動距離が一番小さいものを選ぶようにする
これも「計測時コストを減らしたいのなら自然な発想」だと思います。
ただ、今回は$${P}$$値の種類数が少ないような実装をしたため、事後確率が同じものが大量にできてしまい、結構効き目のある改善となっています。
■配置コストがでかいため、2値から3値に(①)
まず、方針のところに書いた通り、配置をどんな場合でも「どの出口セルのペアにおいても、移動後の位置が差の大きい2値に別れるような移動が存在するような配置にする」ということを念頭に置いていたため、隣接している出口セルが存在する以上、(私の中では)2値の隣接は必須でした。
その上でその条件を満たすように緩衝材として2値の中間値を入れたかったので、「2値の隣接する数を極力減らした上で配置するのはどうすればいいか」を考えた時に閃いたのが下図の①です。
白: 2値の低い値の方
赤: 2値の高い値の方
橙: 2値の中間値。500。
としてやれば、白と赤の配置時コストが発生するのは4箇所まで減ります(中央で2箇所、上下と左右は繋がっているので、そこでそれぞれ1箇所ずつ)
■配置コストがでかいため、3値から5値に(②)
①に合わせて、白と橙、赤と橙の間にも緩衝材として中間値を入れてやれば良いです。①で2値の隣接する数は極力減らせたので、①の状態で支配的になっていたコストは元の削減されたコスト代わりに①で発生したコストでした。これを減らしにいきました。
■2値の隣接する箇所をさらに減らす(③)
よくよく考えると①で書いた「上下と左右は繋がっている」ため隣接している2値は「どの出口セルのペアにおいても、移動後の位置が差の大きい2値に別れるような移動が存在するような配置にする」を達成するためには不要です。接している2値のどちらかを2値の中間値に置き換えました。
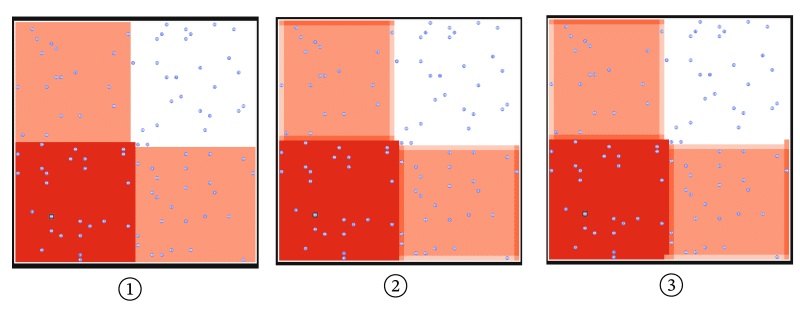
最終解法
計測パートについては「計測で行う処理について」で書いたベイズ推定の方法をベースに、改善フェーズに記載した、
計測処理で、すでに確定した出口セルについては、他のワームホール - 出口セルの計測の時にその出口セルの確率を0にする
計測処理で、ピックアップする事前確率が高い出口セルのペアの候補が複数ある場合に、移動距離が一番小さいものを選ぶようにする
をしています。
あとは配置についてですが、最終的には上図の③のような感じです。
白: 2値に分けた時の低い値
赤: 2値に分けた時の高い値
面積の大きい橙: 中間値。500。
その他: 上の3種類の値のうち2種類と必ず接している箇所で、その2種類の中間値。
他にも細かいことはやっていますが、細かいので割愛します。
