実数は「符号」と「絶対値」の二つの部分から成る。ここでは絶対値を$${0}$$以上の実数と同じものと見なす。

ひとまず符号は後で考えることにして、$${0}$$以上の実数の現実的な解釈の一つを示す。

0以上の実数の具体例

$${0}$$以上の実数に対応する具体的な物として「直線の長さ」がある。

どんな直線の長さでも必ず$${0}$$以上の実数で表すことができ、逆に、すべての$${0}$$以上の実数に対して、対応する長さをもつ直線を実際に引くことができる。これら両方を可能にする道具が「定規」である。

定規で測れば直線の長さを数で表せるし、逆に、好きな数値に対応する長さの直線を引くこともできる。

したがって、$${0}$$以上の実数に対応する直線が具体的に存在する。

ここからは、$${0}$$以上の実数に対応する物として、無限に長い定規を考えることにする。

簡単のため、無限に長い定規を、原点（$${0}$$に対応する点）から右方向に無限に伸びる、目盛付きの半直線と見なす。

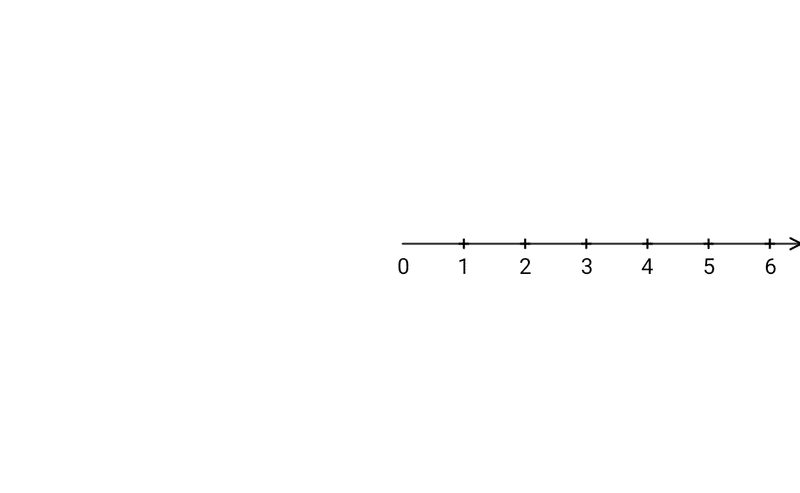
目盛の数字は原点からの距離を示す。原点から望みの長さの数字のところまで線を引けば、望みの長さの線分が得られる。

以上により、$${0}$$以上の実数に対応する具体例として「線分」が実際に存在すること、そしてそれを実際に得るための具体的な方法が示せた。

計算の具体例

$${0}$$以上の実数の計算として、四則計算が定義されているとしよう。四則計算とは、加減乗除、すなわち、

1. 足し算（加法）

2. 引き算（減法）

3. かけ算（乗法）

4. 割り算（除法）

の四つの計算（演算）のことである。

最初に、足し算に対応する具体的な操作を考えよう。

$${0}$$以上の実数$${a,b}$$の足し算$${a+b}$$に対応する操作について考える。

これは、長さ$${a}$$および$${b}$$の線分を用いて、長さ$${a+b}$$の線分を作る操作である。そのような操作として、線分を並べてつなげる操作が考えられる。

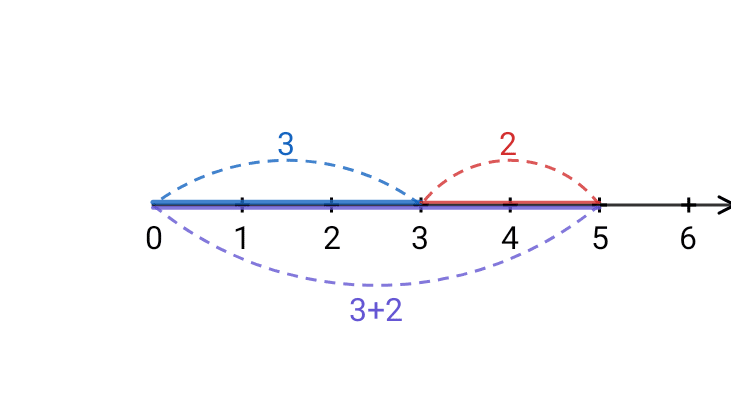
したがって、足し算に対応する具体例として、線分をつなげる操作が存在する。「線分」の世界において、足し算は線分をつなげることだと解釈できる。

引き算に対応する操作についてはどうだろうか。

$${a>b≧0}$$に対して定義される引き算$${a-b}$$に対応する操作は、どのような操作か。

長さが$${a}$$および$${b}$$の線分を用いて長さ$${a-b}$$の線分を作る操作として、長さ$${a}$$の線分から長さ$${b}$$の線分を切り取る操作が考えられる。

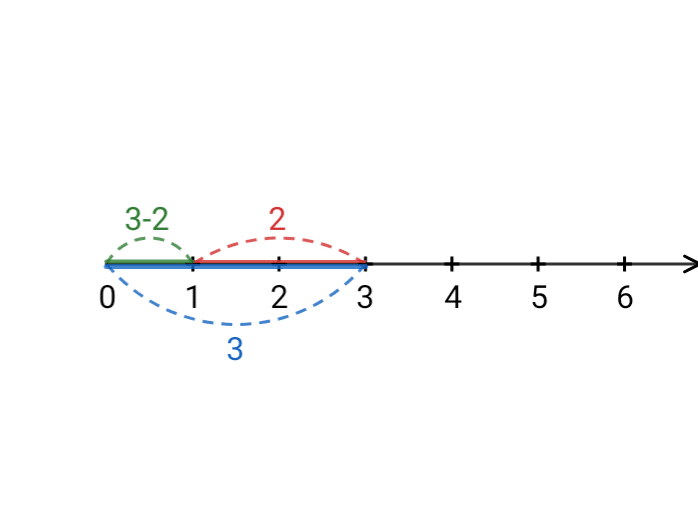
したがって、引き算に対応する具体例として、線分を切り取る操作が存在する。引き算は線分を切り取る操作として解釈できる。

次に、かけ算$${a×b}$$に対応する操作を考えるわけだが、これは少々やっかいである。

結論から言えば、$${a×b}$$に対応する操作は、長さ$${a}$$の線分を倍率$${b}$$で伸び縮みさせる操作である。

倍率$${b}$$で伸び縮みさせる具体的な方法を簡単に説明する。

長さ$${b}$$について、単位長さ$${1}$$と比較していくつ分か数える。例えば、$${2}$$と$${\dfrac34}$$だったとしよう。

長さ$${a}$$をそれと同じ数、すなわち$${2}$$と$${\dfrac34}$$個並べてつなげる。$${a}$$が$${2}$$個分と$${a}$$を$${4}$$等分したものが$${3}$$個分である。

つなげた長さが$${a×b}$$となる。

割り算$${a÷b}$$については逆数のかけ算をすればいい。$${a×\dfrac1b}$$である。

かけ算と割り算に対応する操作は、一方の長さに対応する倍率で他方を伸び縮みさせることである。

これで、四則計算すべてに対して、具体例と解釈が与えられた。$${0}$$以上の実数とその計算は、実在する長さとその操作を忠実に表すことができる。

したがって、$${0}$$以上の実数と四則計算は、現実的かつ具体的な解釈が存在する数体系であり、実在する数といえよう。