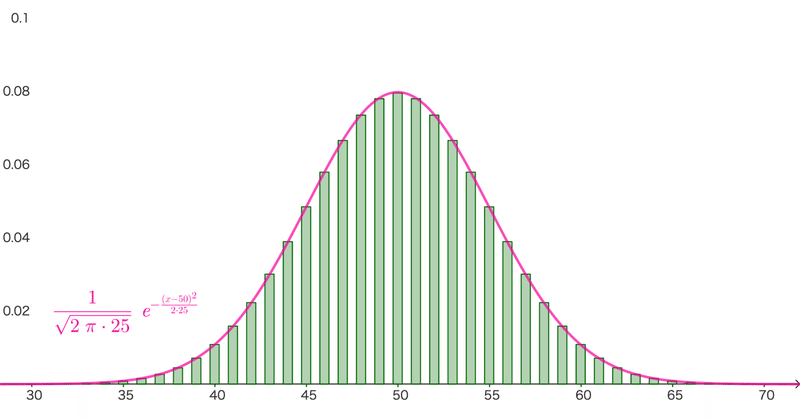
かなり雑だがまあまあ短い、二項分布の極限が正規分布になる証明
統計学の始めの方で必ず、「二項分布のnを無限まで飛ばすと正規分布になります」という説明があります。
確かに、絵で見ると、一目瞭然です。
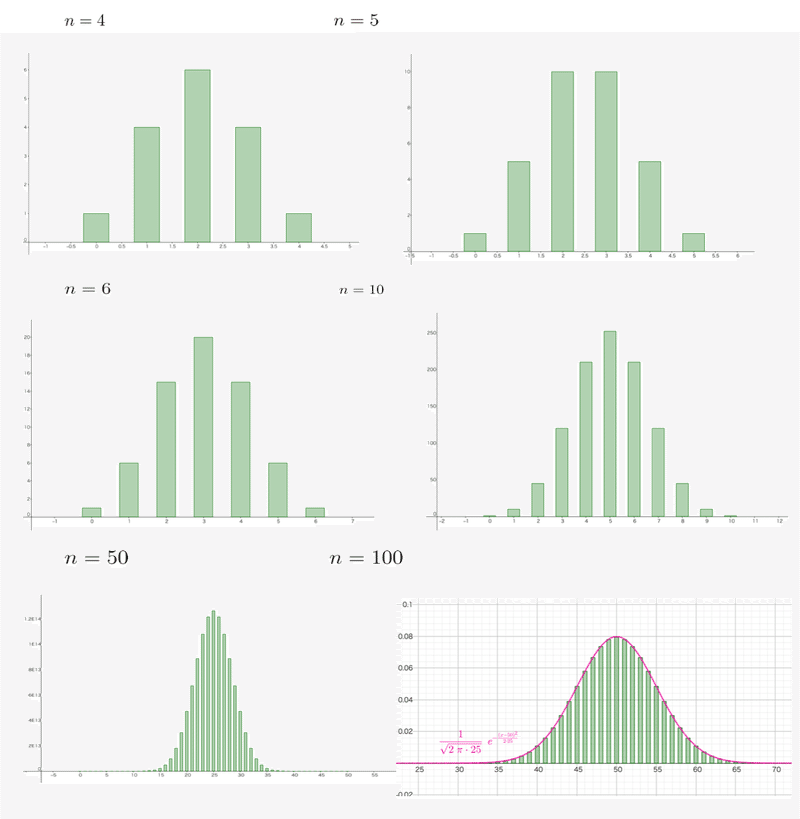
しかし、離散的(飛び飛びの値を取る)な二項分布の式と、連続的な正規分布の式は、似ても似つかないものです。
$$
f(k)=\dfrac{n!}{k!(n-k)!}p^k(1-p)^{n-k} <二項分布>
$$
$$
f(x)=\dfrac{1}{\sqrt{2\pi}\sigma}e^{-\dfrac{(x-\mu)^2}{2\sigma^2}} <正規分布>
$$
初心者は当然、一体どうやってこの両者が結びつくのか見当もつかない。理解するのを諦めて鵜呑みにするか、それとも頑張って、大学数学に近い内容の理解を迫られる地獄に突入するのか、途方に暮れるのか、選択を迫られます。
高校数学は鵜呑みの立場のようです。積分が使えない中学生の数学授業での「円錐の体積は低面積×高さの1/3、同じ高さの円筒に円錐容器から水を注いで、ほら3杯で満タン」を思い起こさせます。仕方ないがそれでいいのかなあ。
さて、本件の証明は、nが大きい時に階乗を近似できるというスターリングの公式$${n!=n^n e^{-n} \sqrt{2\pi n}}$$を用いてゴリゴリに計算するのをよく見かけますが、これがなかなか難しく、「ふーん、そうなのね」と現実逃避を余儀なくされます。
ここでは、もう一つのメジャーなド・モアブル=ラプラスの定理に近いと思われる証明をしますが、上のリンクは初心者にとって命綱である式変形が省略されているようで(こちらの見落としもあるかも知れませんが)、その補完も兼ねてまあやってみましょう。多分、スターリング方式よりは感覚的に掴みやすいのではないかと思います。
証明のあらすじ
扱いにくい二項定理の中の階乗を、隣同士の割り算で消し、身綺麗にする。
1を引いて隣同士の差を作ると、差分商(聞き慣れないが大丈夫)の形が現れる。
隣同士ならどこでも良いらしい(少し怪しい)ので、平均辺りを選択すると、分母が分散$${\sigma^2}$$になる。平均$${np}$$も$${\mu}$$に書き換える。
差分商を離散微分として微分方程式の形に持っていく。
これを解いて終了。但し、係数部分はガウス積分に丸投げ。
証明
1.身綺麗にする。
まず、二項分布のお隣さん同士、$${k,k+1}$$番目ですね、これを割り算します。つまり、隣同士の間の比をとる訳ですが、当然単なる定数にはならず関数になります。
以下、$${1-p}$$を$${q}$$と手抜きして見やすくします。
$$
f(k)=\dfrac{n!}{k!(n-k)!}p^kq^{n-k},\\
f(k+1)=\dfrac{n!}{(k+1)!(n-k-1)!}p^{k+1}q^{n-k-1}
$$
なので、$${f(k)}$$の方をひっくり返して掛けて、
$$
\begin{align*}
\dfrac{f(k+1)}{f(k)}&=\dfrac{n!}{(k+1)!(n-k-1)!} \cdot \dfrac{k!(n-k)!}{n!} \cdot \dfrac{p^{k+1}q^{n-k-1}}{p^kq^{n-k}}\\
&= \dfrac{n-k}{k+1} \cdot \dfrac{p}{q}
\end{align*}
$$
おお、かなりスッキリ、身綺麗になりましたね。
厄介でパワフルなビックリマークが消えてなくなりました。よかった。
そして、隣同士の比の中に$${\dfrac{1}{k}}$$があるので、これは恐らく$${\log}$$っぽくなるだろうと見当が付きます($${\log x}$$の微分が$${\dfrac{1}{x}}$$なので)。
2.差分商を作る。
差分商、聞き慣れないですよね。私も初めて知りましたが、要するに、微分を高校で初めて習うときにやるこいつ
$$
\lim_{h \to 0}\dfrac{f(x+h)-f(x)}{h}
$$
の、$${\lim_{h \to 0}}$$を除いた右側のことだそうです。微分の考え方のやや荒っぽい奴ですね。確かに差分をとって、その変化量で割っているので「差分商」で間違いありません。
そこから変化量をゼロに飛ばせば、「微分商」つまり見慣れた微分係数に進化する訳です。
これを作るには、やや天下り的ですが、$${\dfrac{f(k+1)}{f(k)}}$$から$${1}$$を引けばもう出来上がり。
$$
\begin{align*}
\dfrac{f(k+1)}{f(k)}-1&=\dfrac{1}{f(k)} \cdot \dfrac{f(k+1)-f(k)}{1}\\
\end{align*}
$$
$${\dfrac{f(k+1)-f(k)}{1}}$$の部分が差分商になります。確かに、差分/変化量になっています。
そして少しネタバレすると、左の余計な感じの$${\dfrac{1}{f(k)}}$$が、最後の仕上がりで対数$${\log}$$を経由してネイピア数$${e}$$が出てくる伏線になるのです。
具体的に計算してみます。
$$
\begin{align*}
\dfrac{f(k+1)}{f(k)}-1&=\dfrac{np-kp-kq-q}{(k+1)q}\\
\dfrac{1}{f(k)} \cdot \dfrac{f(k+1)-f(k)}{1} &=\dfrac{np-k-q}{(k+1)q}
\end{align*}
$$
変形時に、$${-kp-kq=-k(p+q)=-k}$$を使いました。
3.平均あたりで勝負する。
出来上がった上式右辺ですが、二項分布でお馴染み、平均$${\mu=np}$$、分散$${\sigma^2=npq}$$で置き換えます。
このとき、「同じ関数なら微分はどこでやっても良い」という(実は確証はないが結果オーライ)前提のもと、$${k+1=np}$$、つまり、平均値(の隣)で勝負することにすると、
$$
\dfrac{np-k-q}{(k+1)q}=-\dfrac{k-\mu+q}{npq}=-\dfrac{k-\mu+q}{\sigma^2}
$$
と、分母が分散となります。更に、分子に一人ぼっちで残った$${q}$$ですが、これは実際には$${\dfrac{1}{2}}$$とか$${0.3}$$とかの$${1}$$以下の値であり、$${100}$$とか$${1000}$$とかの値を取るべき足し算の他のメンバー$${k,np}$$と比べると無きに等しい、よってサヨナラします(カッコよく言うと近似)。すると結局、
$$
\begin{align*}
\dfrac{1}{f(k)} \cdot \dfrac{f(k+1)-f(k)}{1} &=-\dfrac{k-\mu}{\sigma^2}
\end{align*}
$$
という式が出来上がります。右辺は正規分布の右肩っぽいですよね。もうここまで来ました。
4.差分を微分に。
離散微分の考え方は、変化量($${h}$$とか$${\Delta x}$$と書かれるやつ)をゼロに近づけるのではなく、1を変化量とし、全体が大きくなれば1が相対的に小さくなるので、微分と同じこと、ということと解釈しても間違いではないでしょう。
ということで、$${k}$$を大きくすると、差分は微分に進化できるので、そうします。ついでに、変数も整数っぽい$${k}$$から連続っぽい(そんな決まりはありませんが、雰囲気です)$${x}$$へと進化させます。
$$
\begin{align*}
\dfrac{1}{f(k)} \cdot \dfrac{f(k+1)-f(k)}{1} &\\
=\dfrac{1}{f(x)} \cdot f'(x)&=-\dfrac{x-\mu}{\sigma^2}
\end{align*}
$$
これで微分方程式
$$
\begin{align*}
\dfrac{1}{f(x)} \cdot f'(x)&=-\dfrac{x-\mu}{\sigma^2}
\end{align*}
$$
が得られました。あとはこれを解くだけです。
5.微分方程式を解く。
微分方程式は高校ではとうにやらなくなっていて、高校生はお手上げ…という訳ではありません。「微分方程式を解く」とは要するに、「関係式にうまく当てはまる関数を見つける」だけのことです。積分でもよくある「なんせ見つかれば結果オーライ」。
結論、左辺は$${\dfrac{d\log f(x)}{dx}}$$です。$${\log}$$なので上下ひっくりかえし、更に中身を微分したものを掛ける。高校でも習う例の合成関数の微分、(個人的には五月雨微分と呼んでいます)です。
ということで、こうなります。
$$
\begin{align*}
\dfrac{d\log f(x)}{dx}&=-\dfrac{x-\mu}{\sigma^2}
\end{align*}
$$
両辺を積分します。不定積分の定数を$${C}$$とすると、
$$
\begin{align*}
\int \dfrac{d\log f(x)}{dx} dx &=-\int \dfrac{x-\mu}{\sigma^2} dx\\
\log f(x) &=-\dfrac{1}{2} \left( \dfrac{x-\mu}{\sigma^2} \right)^2 \sigma^2 +C\\
&=- \dfrac{(x-\mu)^2}{2 \sigma^2}+C
\end{align*}
$$
なので、右辺は$${e}$$の右肩に乗って(重そう)、
$$
\begin{align*}
f(x) &=e^{- \dfrac{(x-\mu)^2}{2 \sigma^2}+C}\\
&=C'e^{- \dfrac{(x-\mu)^2}{2 \sigma^2}}(C'=e^C)
\end{align*}
$$
できました。
定数部分は丸投げ
上式の$${C'}$$は、正規分布のマイナス無限からプラス無限までの積分結果が1となるように割り戻した$${\dfrac{1}{\sqrt{2\pi}\sigma}}$$になるのですが、この証明で登場するガウス積分はあまりに有名なので端折ります。
代わりにこの積分を見事に可視化した動画を貼り付けておきます。
それでは。
【気になること】
やはり「平均辺りで勝負」が怪しいです。
なんせ変数込みの式を定数に持って行く訳ですからね。
実は色々な証明に当たってみましたが、大体$${\delta = np-k}$$で$${\delta \to 0}$$のような感じで、これって見た目はカッコいいが要するに$${k=np}$$かなあと。
でも結果オーライなのです。スッキリした説明募集中、
この記事が気に入ったらサポートをしてみませんか?
