検定・推定における基本中の基本。正規分布の標準化について解説します。
この問題を考えます。

グラフにするとこんな感じですね。

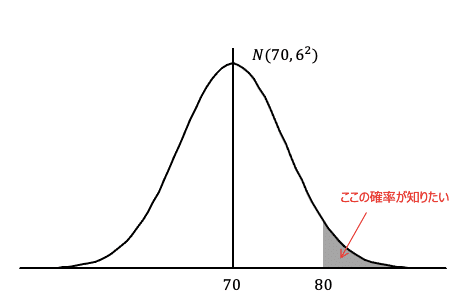
「はい、◯％です。」って即答できる人は少ないでしょう。
というかこのままじゃ分からないんです。
いきなり$${N(70,6^2)}$$の正規分布の一部の確率を求めるとか無理ゲーです。

なので、一つ道具を使います。
「正規分布表」
と呼ばれる表です。これです。

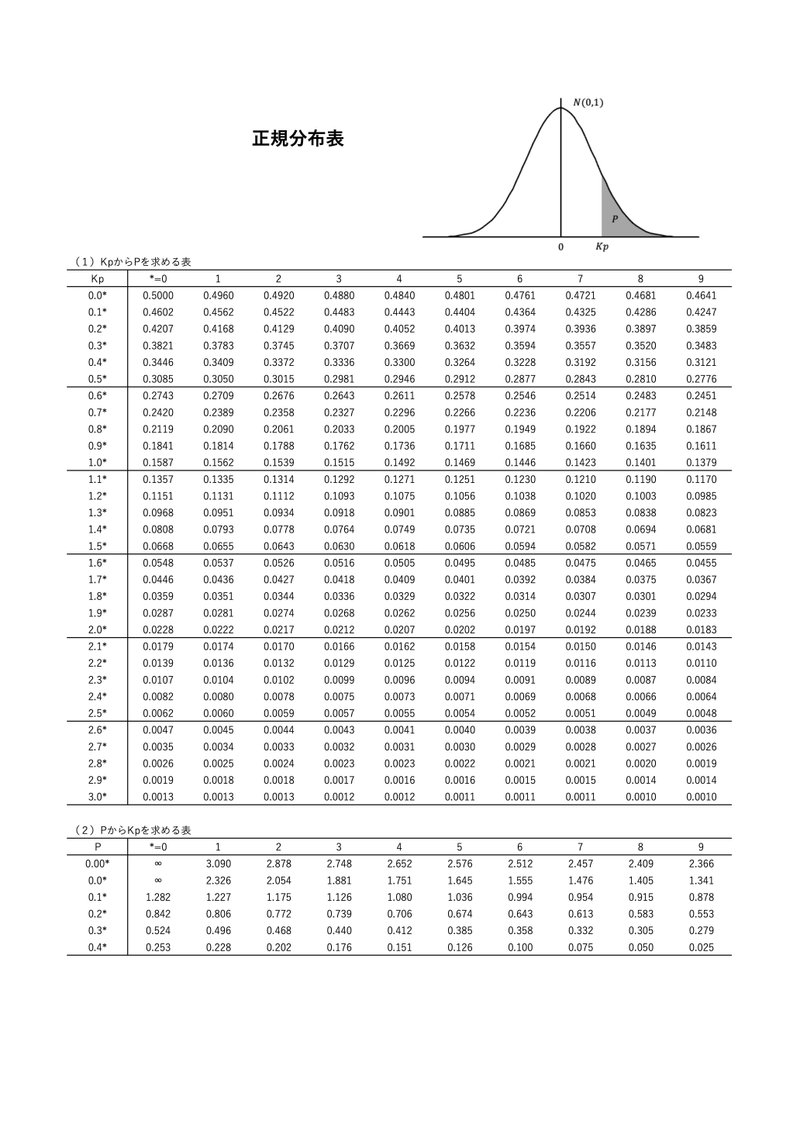
この表は、平均０、分散１の正規分布（決まった書き方をすると$${N(0,1)}$$と書きます）における確率を表にしたものです。
$${Kp}$$ってのが確率を知りたい値です。
表に書いてある数字が確率$${P}$$を表しています。この表の数字を見れば右上のグラフの$${P}$$のエリアの確率が分かるってことですね。

一旦問題を忘れて、例えば、$${N(0,1)}$$の正規分布において、値が２以上の確率を知りたいとします。
グラフにするとこんな感じです。

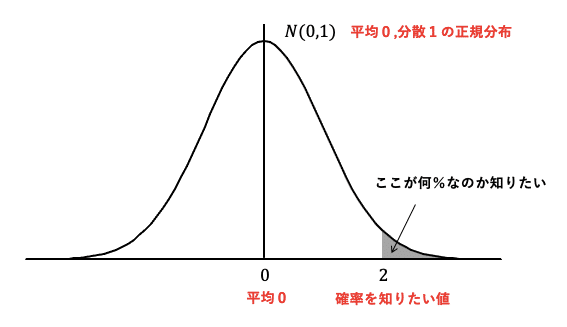
この場合、$${Kp=2.00}$$になります。
なので、正規分布表の$${Kp=2.00}$$を探しましょう。
表の縦が小数点第一位までを表していて、横が小数点第二位の値を表しています。
先ず表の左の縦列から2.0を探します。今知りたいのは2.00のときの確率なので、横は0を探せばいいですね。縦が2.0、横が0の表の交点が2.00のときの確率を表しているってわけです。

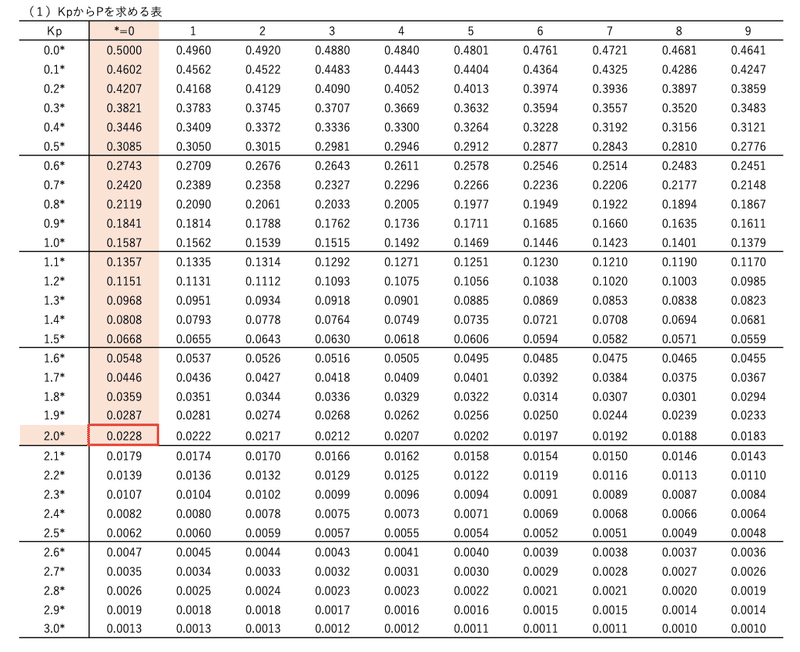
交点の数字は$${0.0228}$$でした。％で表すと、$${2.28\%}$$です。
よって、$${N(0,1)}$$の正規分布において、2以上になる確率は$${2.28\%}$$だよってことが分かったんですね。

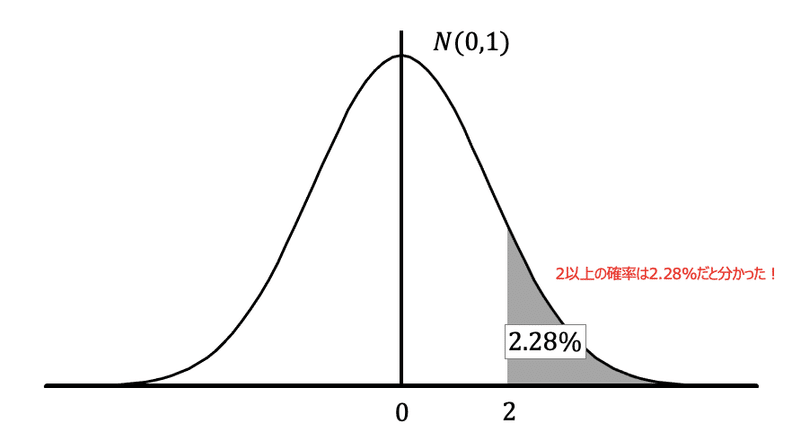
つまり何が言いたいかというと、$${N(0,1)}$$の正規分布であれば、正規分布表っていう超便利な道具を使って知りたい確率を求めることができるんです。

では、最初の問題に戻りましょう。

問題の正規分布は$${N(70,6^2)}$$でした。でも、このままでは正規分布表は使えません。正規分布表を使えるのは$${N(0,1)}$$の正規分布だけなんです。
「じゃあ、どうするんじゃ」
と。
そうです。
$${N(70,6^2)}$$の正規分布を$${N(0,1)}$$に変換しちゃえばいいんです。
これを正規分布の標準化と言います。

標準化の解説に入る前に、正規分布の特徴を一つ。
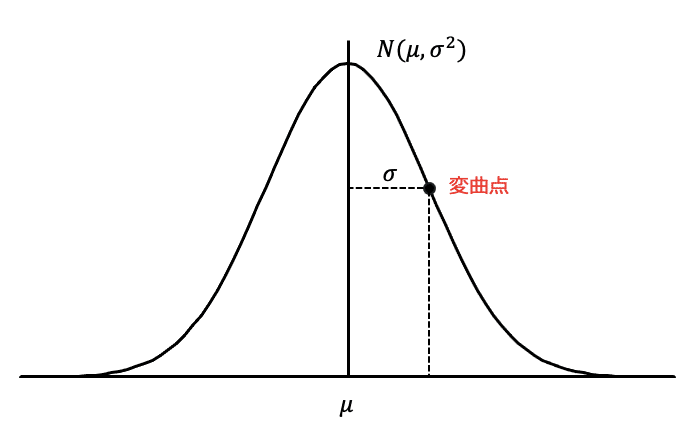
$${N(\mu,\sigma^2)}$$の正規分布では、平均から変曲点までの距離は$${\sigma}$$の値と一致します。（変曲点ってのはグラフのカーブの向きが変わる場所って意味です。）
よく分からなくても大丈夫。今は下の図のイメージだけ見ておいて下さい。
「カーブの向きが変わる場所（変曲点）は真ん中から$${\sigma}$$だけ離れたところにあるんだ」
ってのが分かってれば十分です。

さて、やっと標準化の解説がスタートです。
最初に$${N(0,1)}$$の正規分布のグラフを見てみましょう。

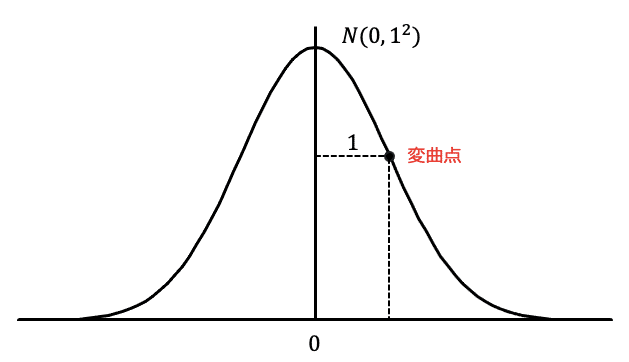
さっき解説したように、変曲点は真ん中から$${\sigma}$$だけ離れたところにあるんでしたね。$${N(0,1^2)}$$の正規分布の場合、$${\sigma=1}$$ですから、真ん中から1離れた場所に変曲点があるはずです。
（今回はあえて、$${N(0,1^2)}$$と書きましたが、前半で書いていた$${N(0,1)}$$と意味は同じです）

$${N(\mu,\sigma^2)}$$と$${N(0,1^2)}$$を見比べてみましょう。

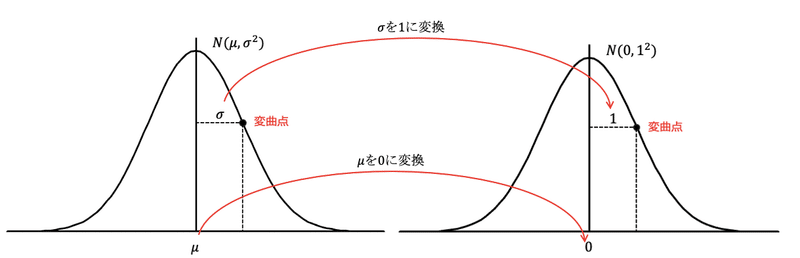
$${\mu}$$を$${0}$$に。$${\sigma}$$を$${1}$$に変換できれば、
$${N(\mu,\sigma^2)}$$を$${N(0,1^2)}$$に変換できる！と言えそうですね。

実際にやってみましょう。
今回の問題は

でしたね。変曲点も入れてグラフを書くとこうなります。

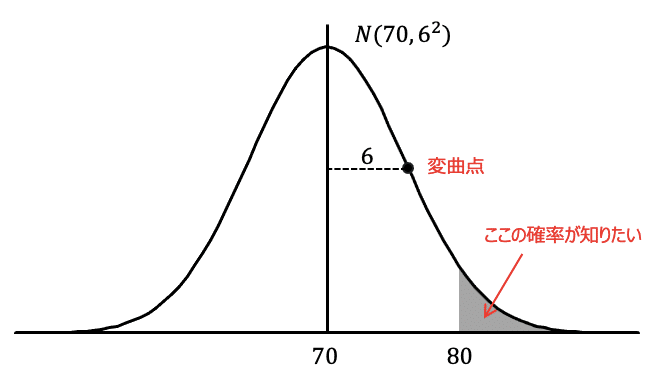
まず、平均を0にしましょう。
今、平均は70ですから、0にするためには70を引けばいいですね。

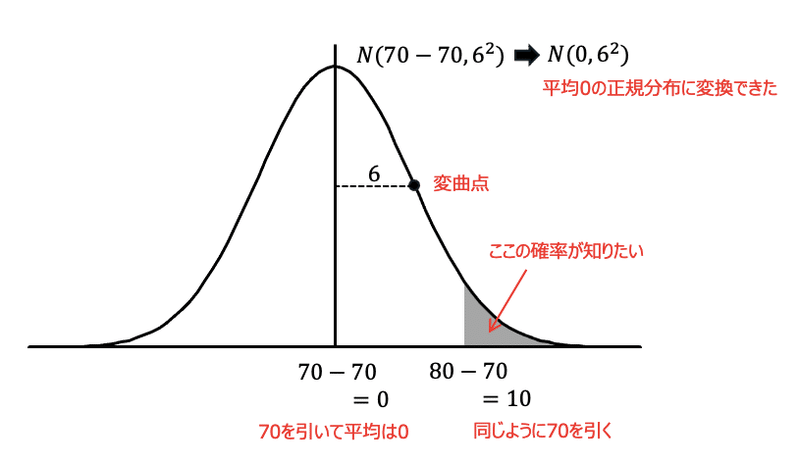
$${N(70,6^2)}$$から$${N(0,6^2)}$$に変換できました。
このとき、元々80だった点は、$${80-70=10}$$になっていることに注目してください。

次に$${\sigma}$$を$${1}$$にしましょう。
今、$${\sigma}$$は$${6}$$なので、$${6}$$で割ってあげれば$${1}$$になりますね。

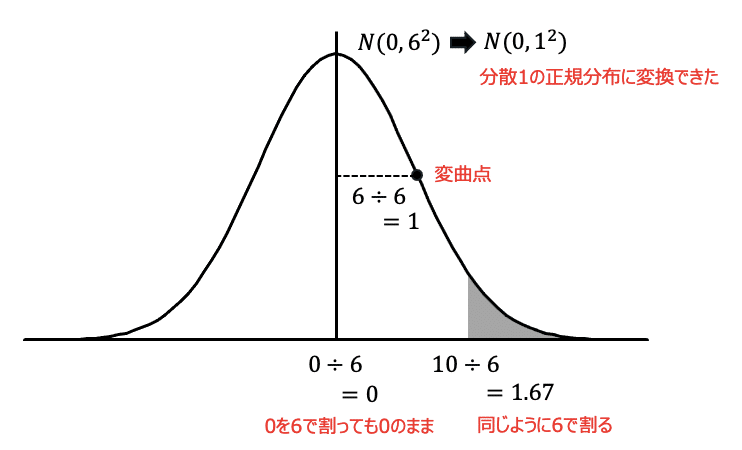
$${N(0,6^2)}$$から$${N(0,1^2)}$$に変換できました。
元々$${80}$$だった点は$${70}$$を引いて$${10}$$になり、更に$${6}$$で割られて$${1.67}$$になりました。
出来上がったグラフを見てみます。

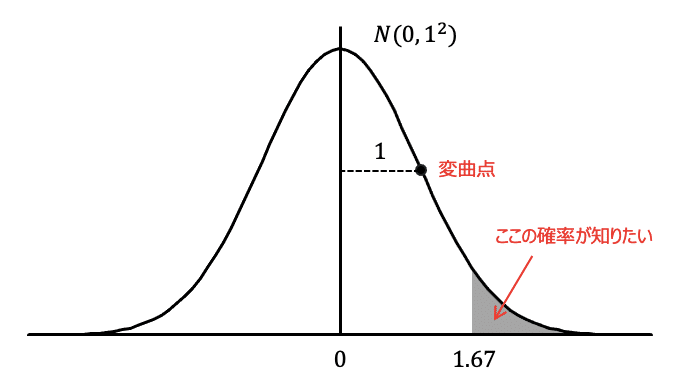
これでバッチリです。あとは正規分布表から、$${Kp}$$の値が$${1.67}$$のときの確率を探せば、求めたい灰色の部分の確率が分かります。

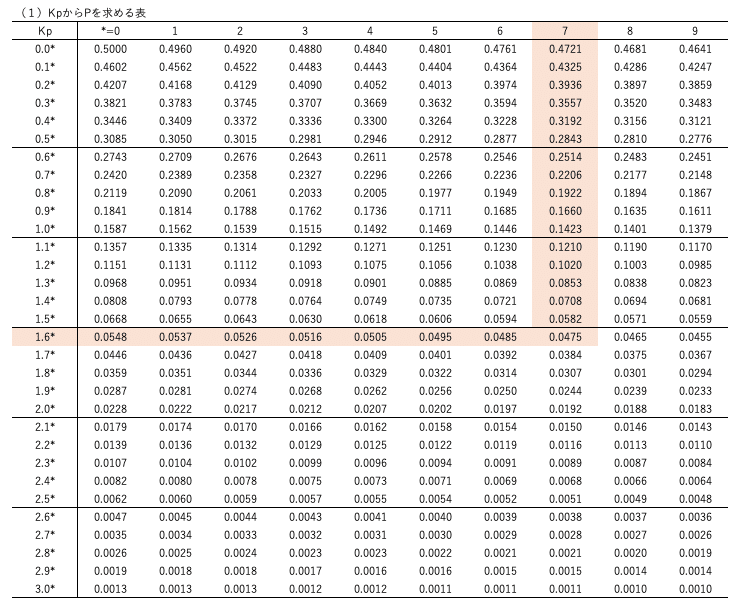
$${Kp=1.67}$$のとき、$${P=0.0475}$$であることが分かりました。
よって、
80点以上の人は上位4.75%である。
が答えですね。

一般式化して考えみます。
$${N(\mu,\sigma^2)}$$のときの求めたい点を$${x_0}$$、標準化した後の点を$${u}$$とします。

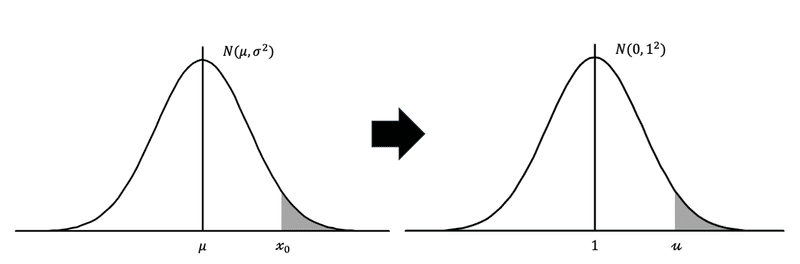
そうすると、$${u}$$はこのように表せます。

$$
u={\cfrac{x_0-\mu}{\sigma}}
$$

これが、テキストによく出てくる正規分布の標準化の式です。
今回の問題で言うと、$${x_0}$$が80で、$${\mu}$$が70。$${\sigma}$$が6でしたね。
$${x_0(80)}$$から$${\mu(70)}$$を引いて、$${\sigma(6)}$$で割ると、標準化できますよって式です。
簡単でしょ。

以上、正規分布の標準化について解説しました。
ここを理解できないと、この先には進めません。標準化を最初に必ず理解して次に進みましょう。