量子力学の勉強をしていると水素原子や水素分子イオン、シュタルク効果などといった項目が並びますが、計算も最終結果も重く、その上どこまで近似できているのかよく分からない近似計算を見せられたりと、今一つ実感が持てない人が多いと思います。そこで数値計算をして色々といじってみるのが有効なはずですが、そういった情報はあまり見つからないように感じます。

以前のアンダーソン局在の記事に引き続き、数値計算の専門家にとっては当たり前すぎてわざわざ教えてくれない話なのかもしれませんが、素人的には興味がある話を書いてみます。水素原子には厳密解もあり、様々なアルゴリズムも存在しますが、この系の持っている特異性が感じられるように非常に一般的な微分固有値方程式として解きました。最後にマセマティカのコードも載せておきます。大学のライセンスが無い人でもクラウド版で無料で試せると思います。

水素原子

数値的な感覚をつかむことが目的ですから、３次元シュレーディンガー方程式の係数を大幅に簡約化して以下の形で考えます。

$$
-\Delta\psi - \frac{1}{r}\psi = E\psi.
$$

対称性から半径rの球内で微分固有値方程式として解き、球面上で波動関数が0となるディリクレ条件を課します。

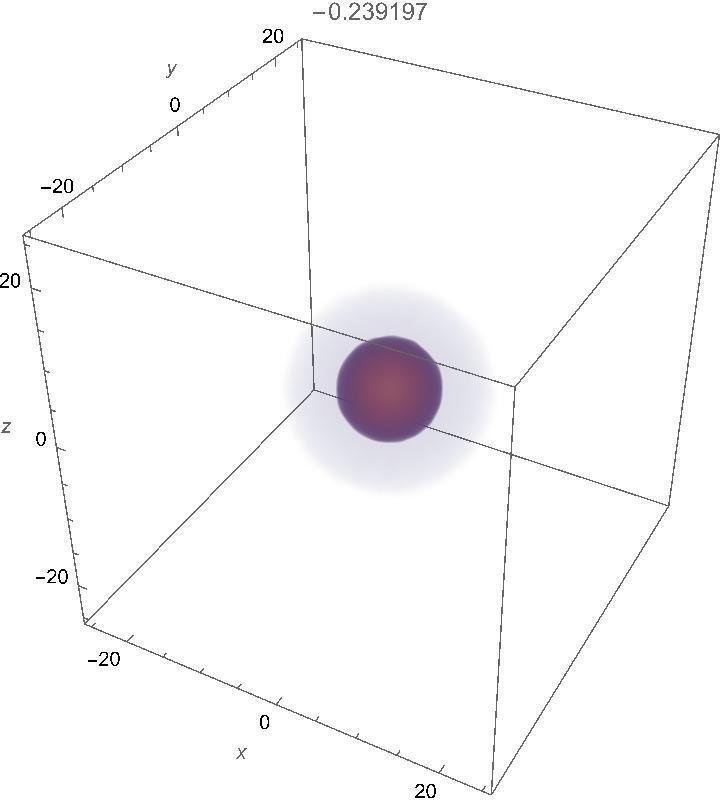
水素原子のエネルギー準位は主量子数nによってn=1,2,3,…とラベル付けされます。以下の数値計算結果からわかるように、基底状態n=1のエネルギーは大体E=-1/4であり、その次の第一励起状態のエネルギーはE=-1/16です。

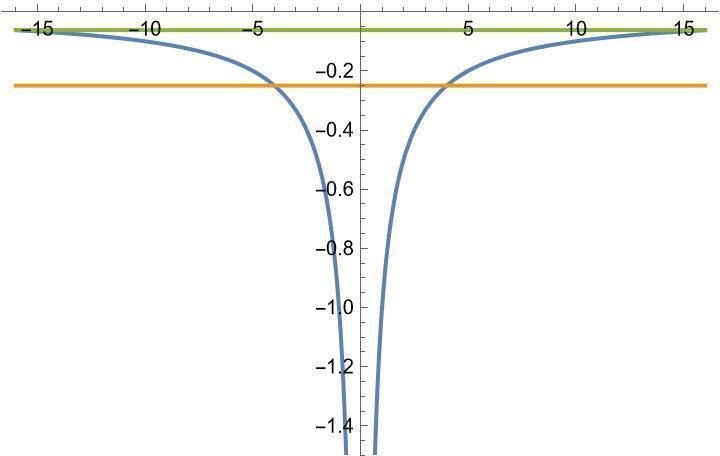
クーロンポテンシャルV(r)=-1/rと比較してみましょう。ポテンシャルがエネルギー-1/4と一致するような場所V(r0)=-1/4はr0=4です。それより大きいrではトンネル効果によって波動関数が急速に減衰しますから、数値計算で必要な領域（教科書の厳密解と違って数値計算では有限な領域をメッシュに切って行います）の大きさの目安は半径4以上の球であると分かります。

第一励起状態と一致するポテンシャルの位置V(r0)=-1/16はr0=16ですから、第一励起状態まで求めたければ半径16以上の球内で数値計算する必要があります。以上の状況をポテンシャルと合わせて描くと以下の通りです。

ここで分かったことは

1. 主量子数が大きくなると急激に巨大な領域で数値計算しなければならなくなる。半径rの球であれば、メッシュの総数はr^3に比例して増加します。必要な半径の目安は4n^2程度ですから、メッシュの数は爆発的に増加していきます。

2. エネルギー準位はポテンシャル上端付近に密集して無限に存在する。数値計算ではこの微小な固有値の違いを検出しなければなりません。

クーロン力が長距離相互作用であるというのは有名な話ですが、こうして数値計算してみるとその言葉の重みがよく分かります。

クーロンポテンシャルの上端付近に解が集中しているということは、有界領域と無限領域のはざまにある絶妙な領域が原子・分子などの物質の住処だということになります。こういう微妙なバランスが多様な物質の姿を生み出しているというのはとても面白いですね。

数値計算の結果として得られたエネルギーを書いておきます。

$$
\begin{array}{c|l}
\hline
主量子数 & エネルギー \\
\hline
n=1 &
-0.2391770\\
n=2 &
-0.0624098, -0.0624037, -0.0623876, -0.0609046 \\
n=3 &
-0.0269521, -0.0269509, -0.0269507, -0.0269470, -0.0269466, \\
& -0.0256887, -0.0256839, -0.0256761, -0.02411\\
\hline
\end{array}
$$

n=2の最後は2s軌道です。教科書どおりだと2s軌道と2p軌道のエネルギーは一致しているはずですが、現在は有限な領域で計算しているので若干ずれているようです。固有値が違うので2s軌道と2p軌道を明確に区別でき、数値計算的にはありがたい性質かもしれません。

以下得られた波動関数を眺めていきましょう。

1s, 2s, 3s軌道

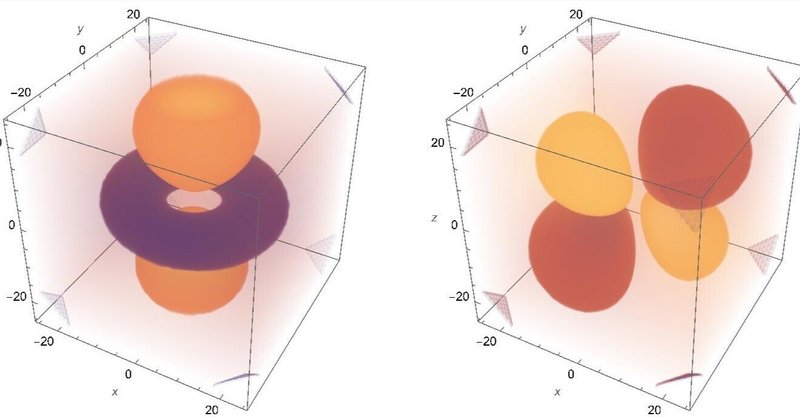
まずは基本のs軌道から、左が1s軌道、右が2s軌道です。図の上側にはエネルギーが表示されています。

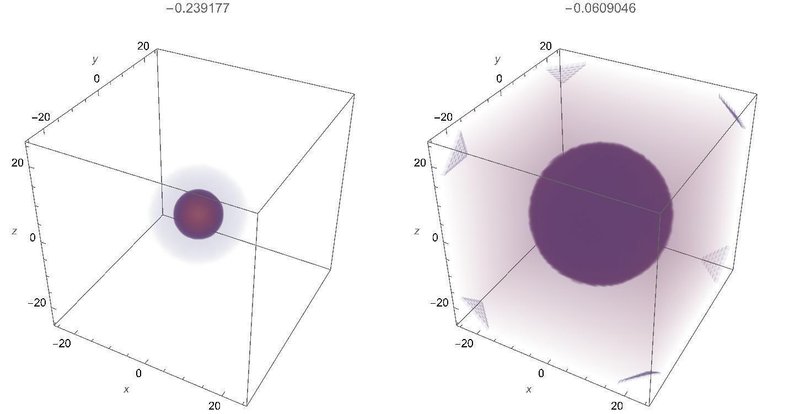
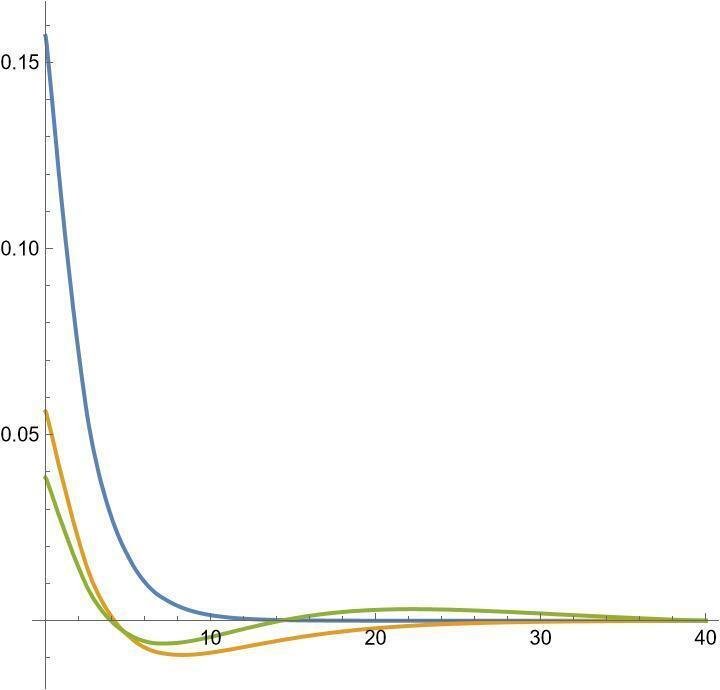
一見して2s軌道の方が大きいのが分かります。数値計算で得られた動径方向の波動関数は以下の通り。波動関数は正規化されていますので、外側に広がった軌道ほど波動関数の絶対値は小さくなります。青が1s、橙が2s、緑が3sです。主量子数が増えるごとに動径方向の節（波動関数が0になる場所）が一つずつ増えていきます。

2p軌道

これは3つ出てきます。x,y,z軸とはちょっとずれていますが、互いに直交する軸を持っているのが分かります。教科書に出ている結果と微妙にずれるあたりが数値計算の実際を表していて興味深いです。p状態は角運動量が1なので、角度方向に一本の節が存在します。

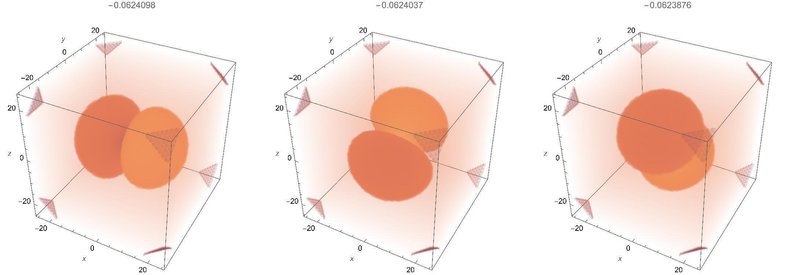
3p軌道

2p軌道と比べて動径方向の節が一つ増えています。角度方向の節が一本なのは同様です。

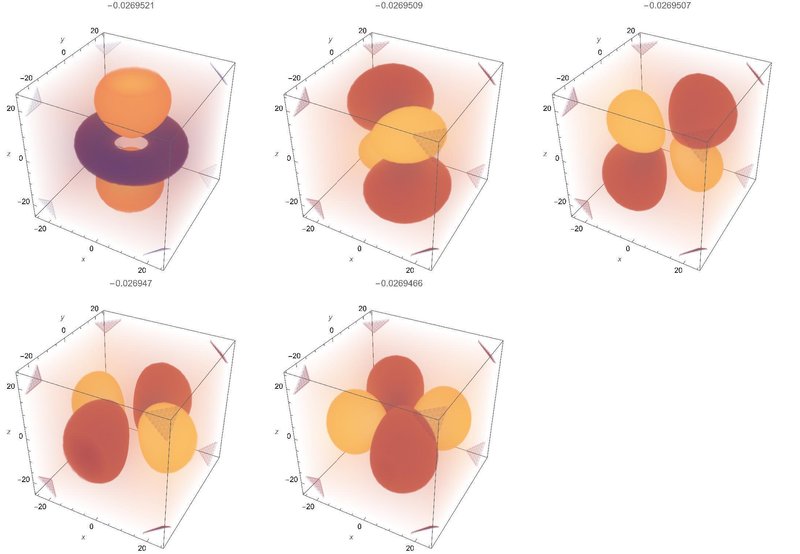
3d軌道

角運動量が2なので2p軌道に比べて角度方向の節が一つ増える（全部で二本）のは予想できますが、一つだけ不思議な形をしたのもきちんと求まっていますね。ちなみに数値計算の精度を下げると最初に求まらなくなるのがこの変わった形の軌道です。

シュタルク効果

物理的な感覚を養うために、水素原子にz方向の電場をかけてみましょう。

$$
V=-\frac{1}{r}+\frac{1}{1000}z.
$$

電場の強さ1/1000は、現在の計算領域の上端で0.4位のエネルギーです。水素原子の基底状態のエネルギーが-0.25なのと比較して理解してください（かなり強いと思います）。これ以上強い電場をかけると、以下の計算結果から想像できるように、高い励起状態では電子がはるか遠くに吹き流されてしまいます。エネルギー固有値は以下の通り。

$$
-0.2391970, -0.0685244, -0.0630621, -0.0630523, -0.0562473, \\
-0.0428802, -0.0373378, -0.0373348, -0.0305170, -0.0305164, \\
-0.0300128, -0.0226541, -0.0226507, -0.0187753.
$$

主量子数１の場合

グラフを見ると水素原子の1s状態と見分けがつきません。エネルギー固有値もほとんど同じです。

主量子数２の場合

以下の四つの状態があります。z軸方向の電場に対して中立的な方向にある、xy平面上の2p軌道はそのままです。一方もう一つの2p軌道は電場によって引っ張られますから、2s軌道とまじりあって（sp混成軌道と呼ばれます）独特な形の固有状態となります。量子力学の計算だと摂動計算の結果として示されますが、直接対角化の結果として同じ結果が得られるのも面白いですね。

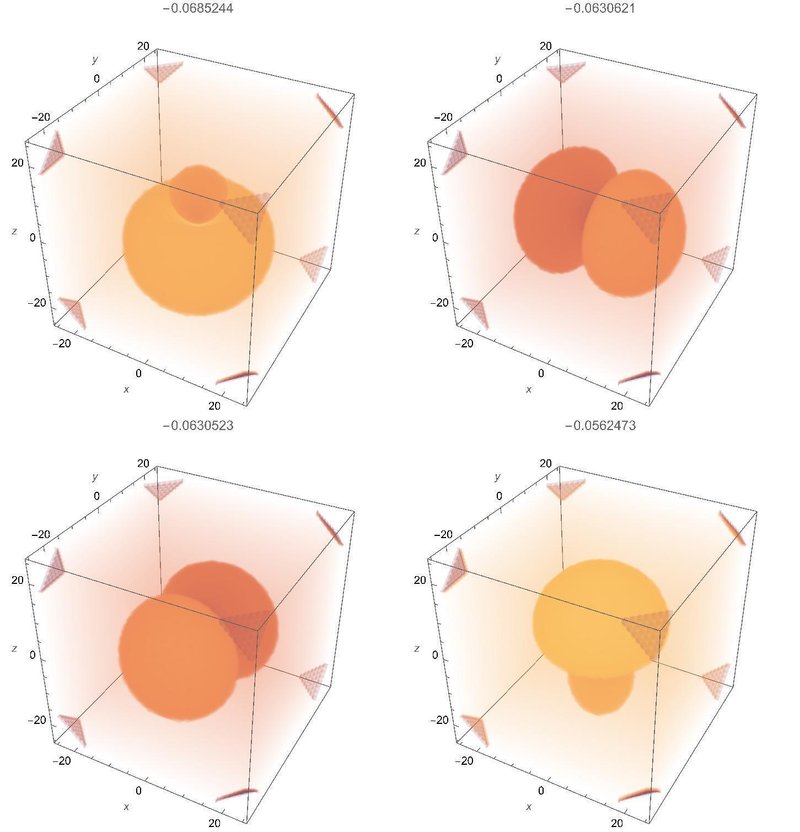
縮退のある摂動論を勉強すると、最初の非摂動波動関数を適切に選択しないとわずかの摂動でも大きな変化が生じることを学びます。ここでの状況では、電場が無い場合の2p軌道は必ずしもxyz軸方向を向いている必要がないのですが（前節の数値計算の状況）、わずかでもz方向に電場をかけると系の向きが定まってしまいますので、xyz軸を向いていない状態から始めると急に大きく変化してしまうことになります。

主量子数３の場合

電場によって全体に下向きに引っ張られた感じです。中立的な方向の軌道はそのまま残っていたり、下向きに引っ張られたり、混成軌道ができていたりと、眺めていて楽しいですね。

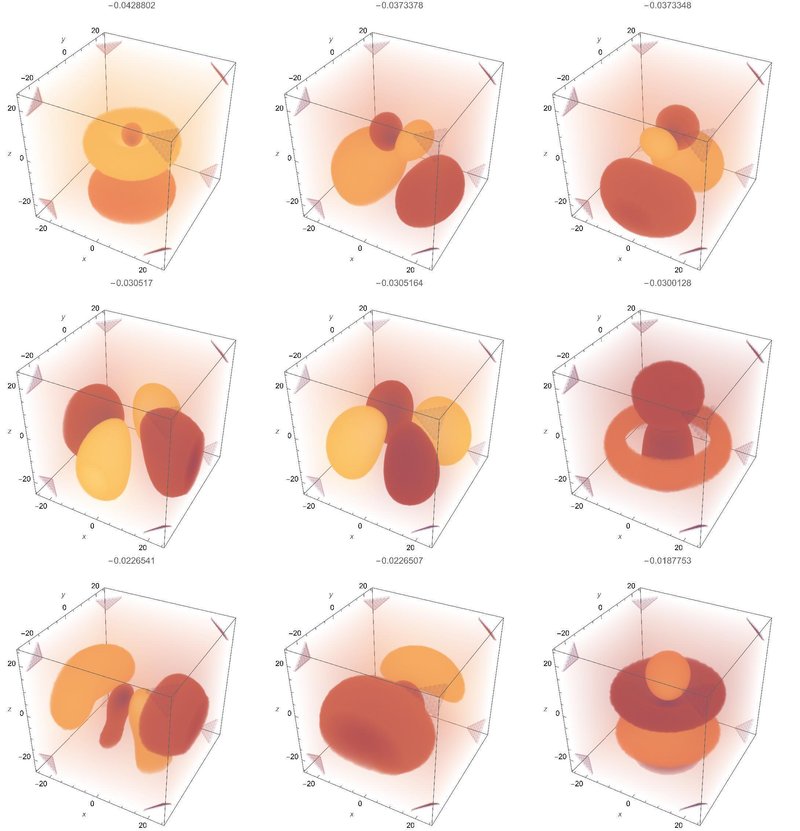
これ以上電場が強いと電子が遠くに流されてしまい、計算領域が広くなって数値計算が困難になります。古典力学とは違った量子力学特有の数値計算の困難さが理解できます。参考までに、古典力学ではカオス現象に代表される困難さが存在します（こちらの記事で考察しました）。

水素分子イオン

化学結合のモデルとして非常に重要です。二つの原子核の周りを一つの電子がまわっていて、最も簡単な共有結合です。物質の成り立ちの基本です。以下のようなモデルで考えます。

$$
V=-\frac{1}{\sqrt{(x+4)^2+y^2+z^2}}-\frac{1}{\sqrt{(x-4)^2+y^2+z^2}}.
$$

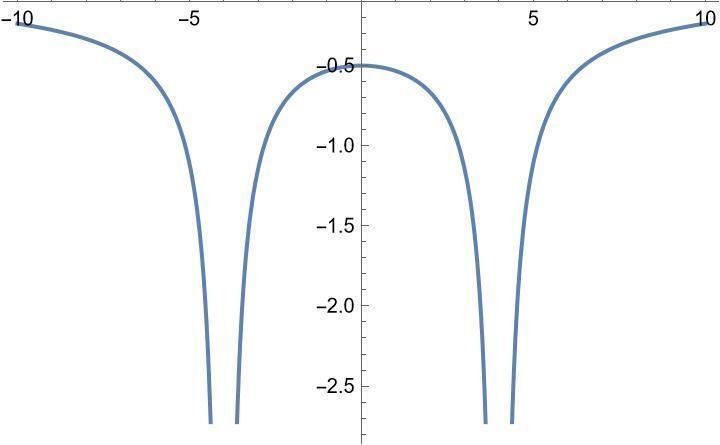
x軸方向のグラフは以下の通り。これ以上原子核を近づけると原点付近がへこんでしまい、真ん中に電子が集まって分子らしくなくなります。本来は原子核同士のクーロン斥力と比較して原子核の位置を決ますが、そこは目分量で済ませます。

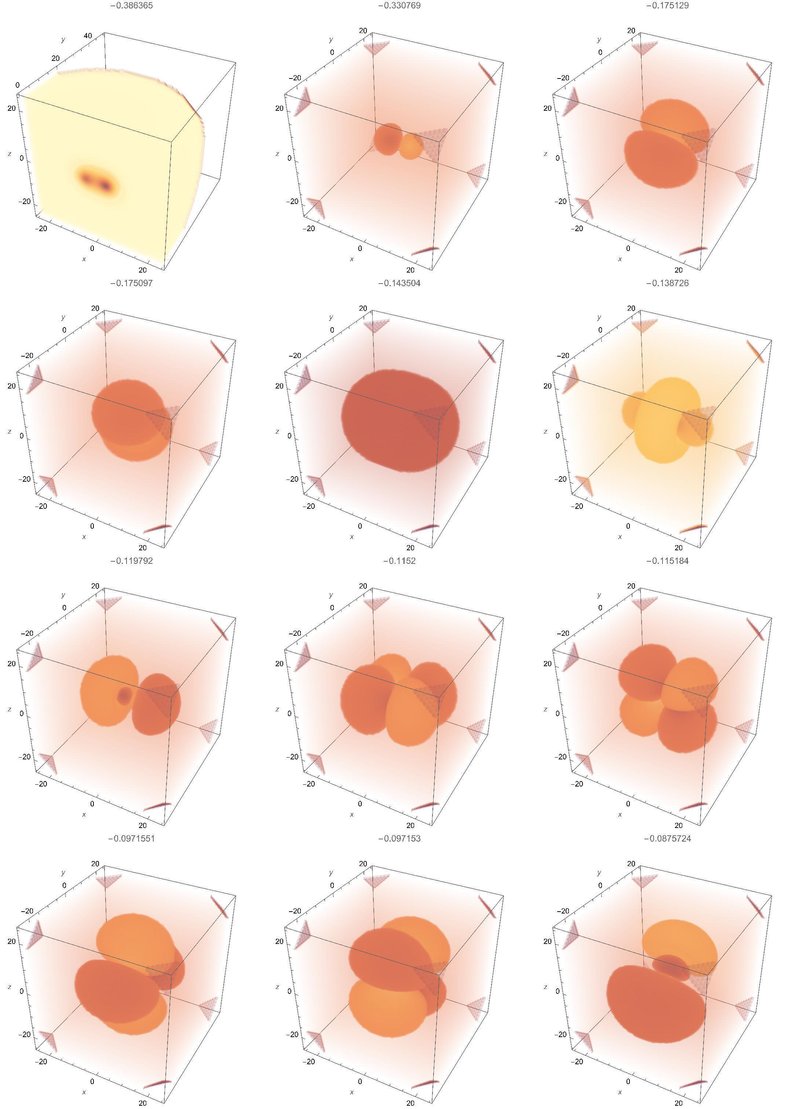
とりあえず下から12個の波動関数を求めると、エネルギー固有値は以下の通り。

$$
-0.386365, -0.330769, -0.175129, -0.1750970, -0.143504, -0.1387260, \\
-0.119792, -0.115200, -0.115184, -0.0971551, -0.097153, -0.0875724
$$

最初のが結合性軌道、二番目のが反結合性軌道ですので、この世の中に化学結合が存在できるのは固有値の差0.05のおかげです。水素原子の基底状態のエネルギー-0.25は現実には-13.6eVで、室温の熱エネルギー0.025eVの500倍程度であり、ここでの固有値の差はその5分の1程度です。かなり強固な結合といえます。

軌道は以下のような形になります。基底状態（化学結合）の図は見にくかったので原点を通る断面を示しました。マセマティカのデフォルトの設定だと、球の中心部で高精度の計算ができるようです。現在は電荷が中心からずれていますので、やや精度の低い計算になっています。特に高い励起状態については参考程度にとどめ、それ以上の使用では理論式やより高精度の数値計算と比較する必要がありそうです。

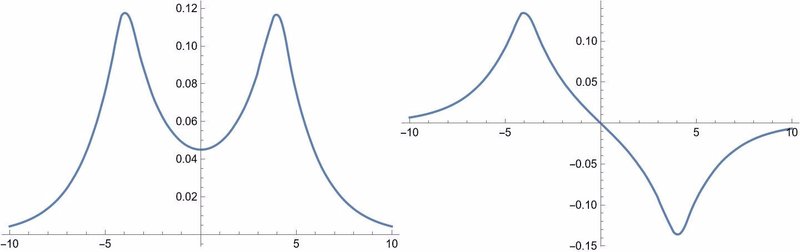
結合性と反結合性軌道をx軸について描いたもの（少し精度を上げて再計算しました）。教科書でよく見るおなじみの図ですが、ここでは微分固有値方程式を直接解いた結果です。普通のノートパソコンで化学結合が作れるのは良い時代ですね。

水素分子イオンのシュレーディンガー方程式は変数分離します。そのため分子系の方程式としては例外的に詳細な解析が行われています。古典力学での対応物はオイラーの二中心問題と呼ばれ、ラグランジュやヤコビも深い研究を行った有名な可積分系です。こちらも数値的に解かせてみるととても面白かったりします。

マセマティカのコード

水素原子の場合を例にとります。ポテンシャルは以下のように定義します。

最後に+1しているのは、バージョン13.3（2023年リリース）時点ではNDEigensystemは固有値を絶対値が小さい順に求めてしまいますので、クーロンポテンシャルの計算をそのまま実行するとおかしくなってしまうためです。ポテンシャルに定数を足しても物理は変わりませんので、あとでエネルギー固有値から1引いて帳尻を合わせることにします。

最初はデフォルト精度で小さめな状況でテストしてみましょう。半径10の球Ball[{0,0,0},10]内で計算し、球面上で波動関数が0になるディリクレ条件を課して最初の5つの固有ベクトルを求めています。これくらいだと一瞬で解が求まるはずです。そしてたった三行のプログラムで本質的な問題を解くことのできるマセマティカプログラミングの効率の良さに驚かされます。

得られた結果はDensityPlot3DまたはContourPlot3Dを使って描画するのが便利です。この段階でポテンシャルの形を修正したり、数値計算のパラメータ（次のコードの下に書いてあります）を見積もっていきます。

ある程度パラメータが絞られたら本気で計算してみましょう。

自分の環境だとまあまあ快適に動きますが、パソコンによってこの設定が重すぎる場合は以下を参考にして数値計算のパラメータを変更してください。メモリーやCPUの使用状況をリアルタイムでモニターしながら調整することをお勧めします。

1. 計算領域の球Ball[{0,0,0},40]の半径40を小さくする。普通は領域を大きくするほど計算精度が向上します。

2. 有限要素法のメッシュサイズMaxCellMeasureを大きくする。デフォルトの分割はかなり大き目のようです。メッシュが小さいほど精度は高くなりますが、小さくしすぎるとメモリー必要量が爆発します。

3. 求める固有ベクトルの総数が14となっているのを減らす。

参考までに、後者の計算で使用したメッシュは以下の通りです。

Pythonとの比較

最近大槻純也先生が「Pythonによる計算物理」という本を出版されました。大変分かりやすい好著だと思いました。ここではマセマティカとの比較を目的に、100ページにある調和振動子のシュレーディンガー方程式を取り上げます。なお計算時間については環境が異なるため、目安程度にお考え下さい（マセマティカの計算時間は10回の平均）。

プログラムの長さ。Python本では59ページと101ページにあるコードを合わせて2ページ弱。一方マセマティカで同等の精度の出力を得るコードは次のようになります。実はマセマティカは補完機能が充実していて、例えばMethodの最初数文字をタイプしただけでその後の構文が丸ごと候補に挙がりますので、実際のタイプ量は更に少ないです。

Pythonと比べてこのプログラムで必要なメッシュの数は15分の1であり、計算時間は21分の1です。またPython本では区間を1000分割して計算していますが、マセマティカで同じメッシュを使用した場合の計算時間は12分の1であり、出力の精度は6万倍向上しました。

マセマティカではメッシュの数が15倍になっても計算時間は1.7倍の増加でした。したがって大規模で複雑な問題であるほど効率が良くなっていくことが期待できます。