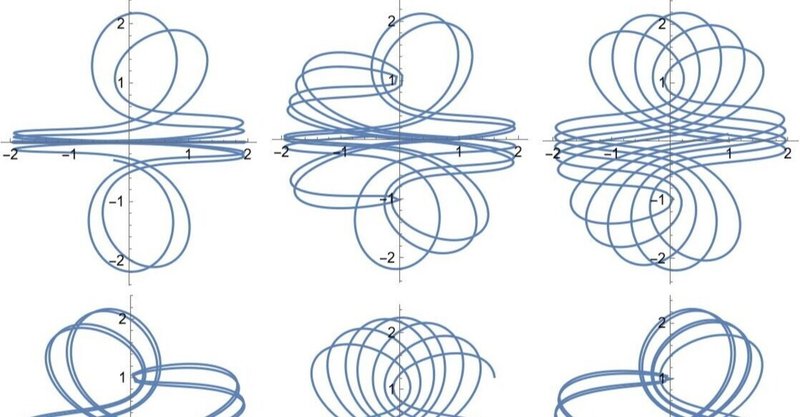
オイラーの三体問題
太陽の周りを一つの惑星が回っているとき、運動方程式の解が楕円などで与えられることはよく知られています。ここで考えたいのは、もし太陽が二つあったらどうなるだろうか?という問題です。一年に二回夏が来るくらいで大したことはないだろう、ですって? いえいえ、実際には目が回るほどもの凄い運動になってしまいます。そんな惑星に住んでいたらさぞかし大変だろうと思うのですが、解を眺めるだけならとても楽しい気分になれます。
歴史
歴史に興味の無い方は、この項目は飛ばして下にあるアニメーションを眺めて下さい。
多くの数学者が同じ事を思っていると思うのですが、こういう面白い問題の歴史を調べるとオイラーの名前が最初に出てくることがしょっちゅうです。この場合もまさにその通りで、オイラーが最初に運動方程式を解くことができること(変数分離すること)を示しました。非常に巧妙な変換をいくつも利用した大変な計算であったようです。これは1760年から1767年にかけての研究です。
L. Euler, Un corps étant attiré en raison réciproque quarrée des distances vers duex points fixes donnés, Mémoires de Berlin (1760), p.28.
L. Euler, De motu corporis ad duo centra virium fixa attracti, Novi Commentarii Academiae Scientiarum Imperialis Petropolitanae, (i) Tome X (1764/65), p.207; (ii) Tome XI (1765/67), p.152.
その間に弟子筋のラグランジュもこの問題に参入し、オイラーの計算を明快にするなどの結果を得ました。両者の研究の過程で、今日楕円座標と呼ばれる素晴らしい数学が発見されました。楕円座標は古典力学や量子力学で色々と役に立ちます。
この問題でもう一人名前をあげたい数学者はヤコビです。オイラーたちの時代から80年程経った頃に、ハミルトン・ヤコビ方程式を応用する方法で変数分離を実行しました。その結果は有名な1843年の講義録に記載されています。前期量子論の頃にパウリなどが参照した結果です。楕円座標とハミルトン・ヤコビ方程式を組み合わせて変数分離する方法は多くの解析力学の教科書でも紹介される、標準的な手法となりました。
こうして方程式を分離しても、解を明示的に書き下そうとすると複雑な積分を計算しなければならなくなり、実際には大変な問題になります。解が非常に複雑な挙動を示すことは広く知られていましたから、筆者も「随分難しい問題があるものだ」などと思っていました。実際かのオイラーやヤコビですらできなかった計算ですから、迂闊に手を出せる問題ではないのは明らかです。
ですので、2008年に最後まで計算をやりきった結果が出たときには大変感心しました。
Diarmuid Ó Mathúna, Integrable systems in celestial mechanics, Birkhäuser, (2008), 234 pages.
ページ数からもすごさがご理解頂けると思います。前書きによると1960年代から取り組んでいたそうです。Ó Mathúna先生は1934年生まれだそうですので、まさに人生をかけたお仕事ですね。きちんと勉強するのは大変そうですが、この本には詳細な歴史的導入が書いてあり、その部分だけでも楽しむことができます。なお、ウィキペディアの記事にも歴史的経緯や色々な結果が出ていて参考になります。
もう一点補足しておきますと、ハミルトン・ヤコビ方程式を用いることから想像がつくように、この問題の量子力学版も数学的には良い性質を持っています。実際、楕円座標を用いると、対応するシュレーディンガー方程式を変数分離することができます。
L. Pauling, The application of the quantum mechanics to the structure of the hydrogen molecule and hydrogen molecule-ion and to related problems, Chemical Reviews 5 (1928), p.173.
二中心問題の量子力学的対応物は水素分子イオンと呼ばれ、化学結合の最も単純なモデルとなっています。
アニメーションについて
この問題の門外漢である筆者がこの記事でやりたいことは、いくつかアニメーションを紹介して多くの方に興味を持って頂くことです。Ó Mathúna先生の膨大な計算と、その結果得られる複雑な解(楕円関数が沢山!)を眺めてもよく分からなかったので、取りあえずパラメータを色々いじって沢山数値計算をしました。色々と解を作ると中には他の方とシェアしたいような魅力的な解が出てきました。そこで旧ホームページで紹介コーナーを作っていたのですが、こちらにも引っ越ししておきます。
三体問題は人知の及ばない複雑な世界ですが、オイラーの三体問題は例外的に解が求まり(可積分系といいます)人間が理解できる領域です。一方で可積分系の中ではとびきり複雑な系です。そうしたユニークな立ち位置の系であることも大きな魅力です。
ご自身でも確認したい読者の為に必要なパラメータも記録しておきます。二つの中心はxy平面の(0,±1)に取り、全ての質量および重力定数は1としました。初期座標(x0, y0)と初期速度(vx0, vy0)を合わせて(x0, y0, vx0, vy0)のように指定します。
アニメーション 1
アニメーションのリンクはこちら
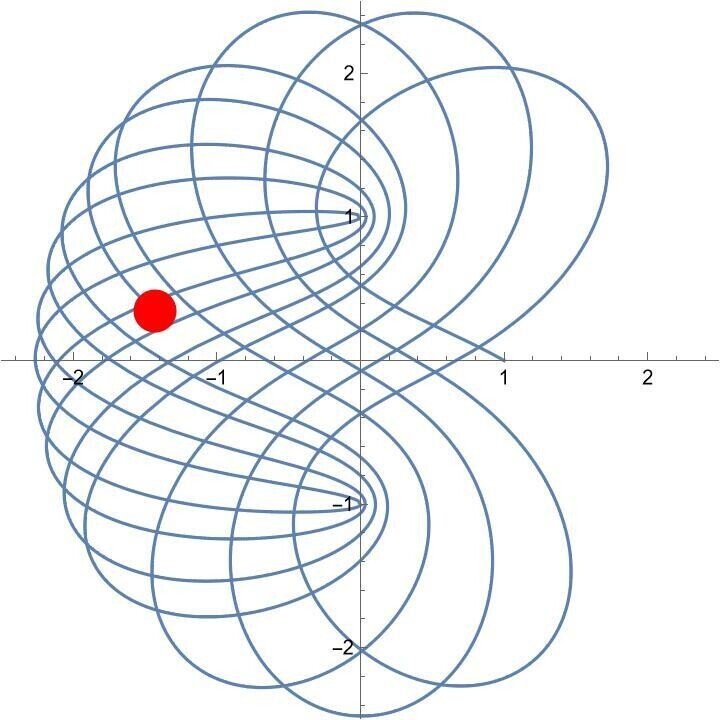
初期値 (1, 0, -1, 0.5624)
アニメーション 2
アニメーションのリンクはこちら
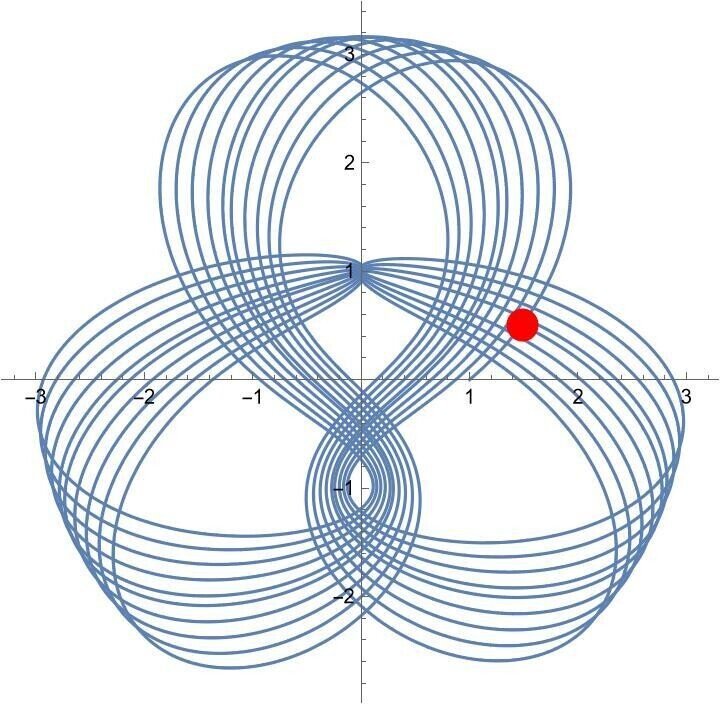
初期値 (1, 0, 1, 0.84)
アニメーション 3
アニメーションのリンクはこちら
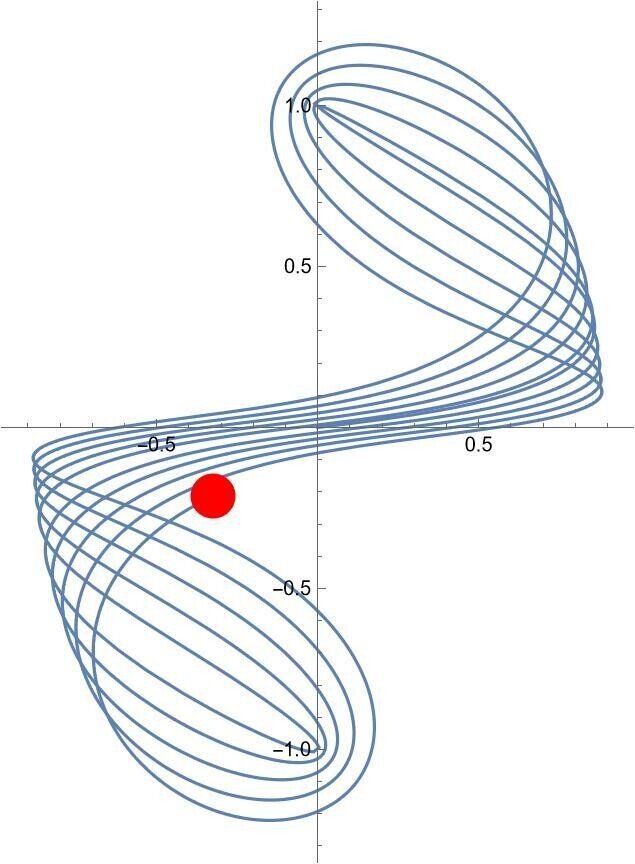
初期値 (0, 0, 1, 0.122)
アニメーション 4
アニメーションのリンクはこちら
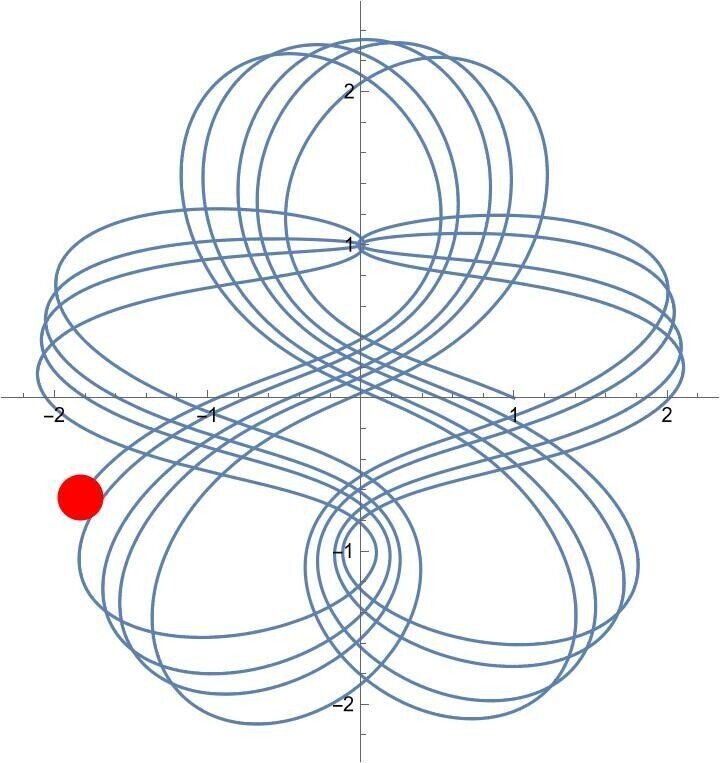
初期値 (1, 0, -1, 0.4337)
アニメーション 5
アニメーションのリンクはこちら
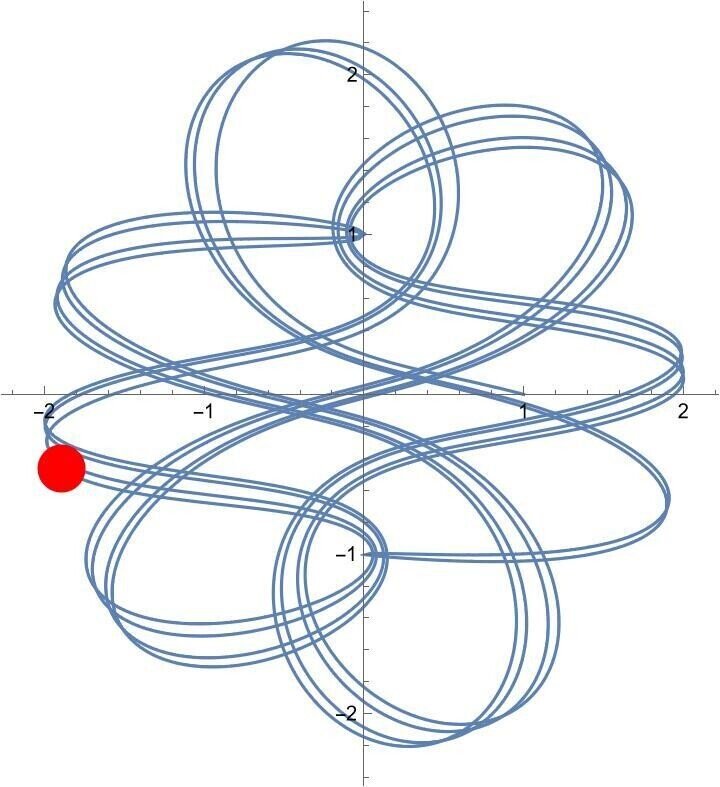
初期値 (1, 0, -1, 0.266)
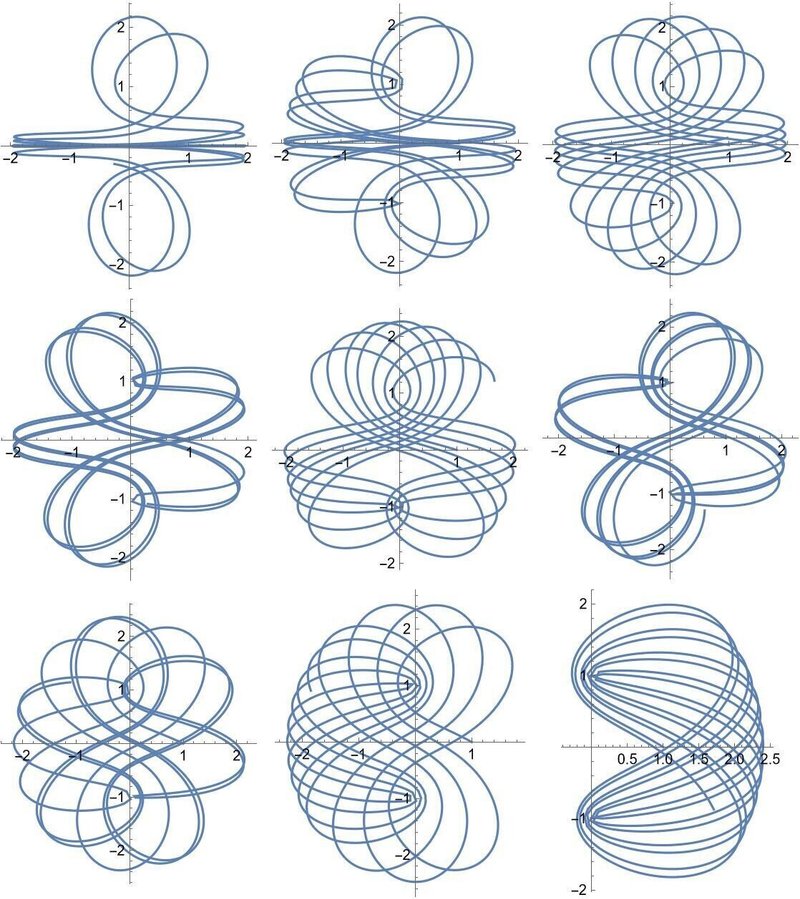
初期値を少しずつ変化させた例
初期値 (1, 0, -1, 0.001 + 0.0802 n) でnを以下のように選びました。
0 1 2
3 4 5
6 7 8
この記事が気に入ったらサポートをしてみませんか?
