データに曲線パターンが見られるときは、直線による回帰ではなく、2次関数や3次関数など説明変数を非線形関数に変換して回帰した方が良い場合がある。

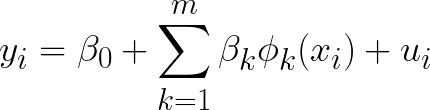
※ φ：基底関数、uiは誤差項

しかし、基底関数をたくさん使って説明変数を増やしすぎると過剰に適合してしまうことに・・・

そこでいい感じに意味のない説明変数を除外してくれるのがLasso・Ridge推定というわけである。

直線モデルの係数推定（解析的なアプローチ）

説明変数の係数がゼロの値に近づくように、一手間加えて係数推定することで意味のない説明変数を洗い出すことができる。

具体的に言うと、正則化項（罰則化項）を加えた二乗誤差関数の最小化問題

とその前に、以下のような直線の式を置いて二乗誤差関数の最小化問題を復習しときます。

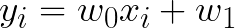
ここで二乗誤差関数を定義すると

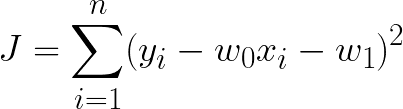
これを最小化することでデータに最も適合する係数が得られる。二乗誤差関数が最小ということは傾きが0になるはずなので、

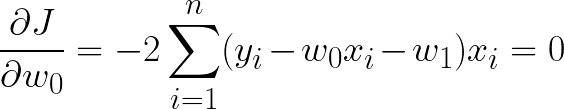
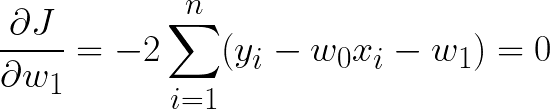
を満たす傾きと切片を見つければよい。

Lasso推定とRidge推定

では、本題のLasso推定とRidge推定とは何か。

結論、λ > 0とする正則化項を加えた二乗誤差関数の最小化問題である。

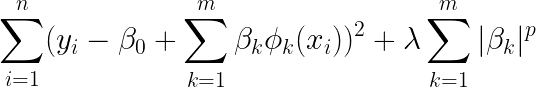
βを大きくしてしまうと正則化項の影響で全体としてはあまり小さくならないので、これを最小化することを考えた時、意味のない説明変数たちの係数はゼロに近づくような効果が期待できるというわけである。

p=1とした時がLasso推定（＝L1正則化）

p=2とした時がRidge推定（＝L2正則化）

である。